Парциальная и относительная парциальная DНSi энтальпии кремния в жидком железе
| Определяемая | Масса добавки кремния, г | |||||||
| 0,392 | 0,242 | 0,260 | 0,533 | 0,358 | 0,365 | 0,540 | 0,513 | |
| Q, Дж | 605 | 392 | 411 | 780 | 526 | 573 | 809 | 780 |
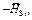 кДж/моль кДж/моль
| 43,2 | 45,4 | 44,3 | 41,0 | 41,1 | 44,0 | 41,9 | 42,6 |
| -DНSi , кДж/моль | 134,3 | 136,5 | 135,4 | 132,1 | 132,2 | 135,0 | 133,0 | 133,7 |
Теория. Парциальная мольная энтальпия 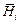 характеризует изменение энтальпии раствора при добавлении к нему бесконечно малого количества компонента i при постоянных температуре, давлении и числах молей п j других компонентов:
характеризует изменение энтальпии раствора при добавлении к нему бесконечно малого количества компонента i при постоянных температуре, давлении и числах молей п j других компонентов:
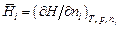 ,
,
где Н - интегральная энтальпия раствора
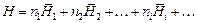 . (1.1)
. (1.1)
Интегральная мольная энтальпия раствора Н m определяется по формуле
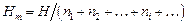 .
.
Из выражения (1.1) следует:
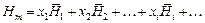 ,
,
где 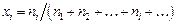 - мольная доля компонента i.
- мольная доля компонента i.
Относительные парциальная DН i и интегральная DН m энтальпии равны:
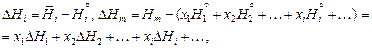
где 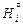 - мольная энтальпия чистого компонента i.
- мольная энтальпия чистого компонента i.
Относительную парциальную энтальпию называют также теплотой растворения, относительную интегральную энтальпию - теплотой образования раствора.
Решение. В калориметре при смешении образца кремния с расплавом железа измеряют тепловой эффект, включающий изменение энтальпии кремния при нагреве от 298 до 1873 К и теплоту образования раствора. Масса растворяемых образцов пренебрежимо мала по сравнению с массой растворителя - железа, поэтому измеряемая величина близка к парциальной энтальпии кремния (т.е. Q » -(¶Н/¶nSi)T, p). Мольную парциальную энтальпию кремния в растворе железа вычисляем по формуле
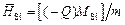 ,
,
где Q - измеряемый в калориметре тепловой эффект смешения образца кремния массой т с расплавом железа (теплота реакции и изменение энтальпии имеют противоположные знаки, поэтому Q имеет знак минус); М - масса моля кремния, равная 28.
Например, для первой добавки кремния (m = 0,392 г, Q = 605 Дж)
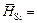 -(605×28/0,392) = -43214 Дж/моль.
-(605×28/0,392) = -43214 Дж/моль.
Относительная парциальная мольная энтальпия кремния
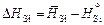 .
.
Для первой добавки кремния DHSi = -43,2 - 91,1 = -134,3 кДж/моль. Рассчитанные величины 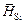 и DHSi приведены в таблице. В исследованном интервале концентраций значения
и DHSi приведены в таблице. В исследованном интервале концентраций значения 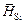 и DHSi не зависят от состава (их разброс не выходит за пределы экспериментальной ошибки). Это указывает на то, что растворы являются разбавленными, поэтому найденные величины
и DHSi не зависят от состава (их разброс не выходит за пределы экспериментальной ошибки). Это указывает на то, что растворы являются разбавленными, поэтому найденные величины 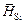 и DHSi представляют собой начальные парциальную и относительную парциальную энтальпии:
и DHSi представляют собой начальные парциальную и относительную парциальную энтальпии: 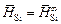 ,
, 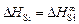 . Вычисляем относительную интегральную мольную энтальпию: DH m = xSiDHSi + xFeDHFe . В области разбавленных растворов DHFe = 0, поэтому DH m = xSiDHSi . Среднее значение DHSi составляет -134 кДж/моль, так что DH m = -134xSi (кДж/моль).
. Вычисляем относительную интегральную мольную энтальпию: DH m = xSiDHSi + xFeDHFe . В области разбавленных растворов DHFe = 0, поэтому DH m = xSiDHSi . Среднее значение DHSi составляет -134 кДж/моль, так что DH m = -134xSi (кДж/моль).
Примечания. 1. Другие парциальные, относительные парциальные и интегральные мольные величины определяют аналогичным образом. Например, парциальная мольная энергия Гиббса, называемая также химическим потенциалом mi, 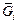 = mi = (¶G/¶ni)p, T, nj ; парциальная мольная энтропия
= mi = (¶G/¶ni)p, T, nj ; парциальная мольная энтропия 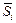 = (¶S/¶ni)p, T, nj ; парциальный мольный объем
= (¶S/¶ni)p, T, nj ; парциальный мольный объем 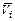 = (¶V/¶ni)p, T, nj .
= (¶V/¶ni)p, T, nj .
2. Парциальная мольная величина характеризует изменение свойства раствора. Она может быть как положительной, так и отрицательной.
3. Если при проведении калориметрического опыта температура растворяемого компонента i равна температуре растворителя, то измеряемая теплота представляет собой относительную парциальную энтальпию DH i . Подогрев добавок является одним из способов повышения точности определения теплот растворения.
2. Избыточные термодинамические величины
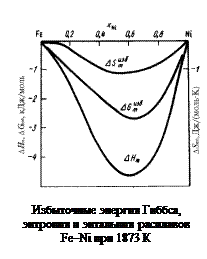
Задача. Определить избыточную энергию Гиббса, избыточную энтропию и энтальпию расплавов Fe–Ni по значениям активностей и теплот растворения железа и никеля.
Исходные данные. Активности железа и никеля (стандартное состояние - чистые жидкие железо и никель) и их теплоты растворения (относительные парциальные энтальпии) в расплавах Fe–Ni при 1873 К [1] представлены в таблице.
| xNi | aNi | aFe | DHNi , Дж/моль | DHFe , Дж/моль |
| 0,1 | 0,073 | 0,899 | –7952 | 218 |
| 0,2 | 0,147 | 0,799 | -10124 | 589 |
| 0,3 | 0,222 | 0,695 | -10172 | 592 |
| 0,4 | 0,294 | 0,593 | -8865 | -160 |
| 0,5 | 0,387 | 0,479 | -6891 | -1844 |
| 0,6 | 0,493 | 0,351 | –4704 | –4462 |
| 0,7 | 0,626 | 0,225 | –2680 | –8238 |
| 0,8 | 0,762 | 0,124 | –1127 | –12853 |
| 0,9 | 0,889 | 0,050 | –246 | –18082 |
Теория. Избыточные термодинамические величины характеризуют отклонение реального раствора от идеального. При образовании идеального совершенного раствора энтальпии компонентов не изменяются, так что мольная энтальпия бинарного совершенного раствора
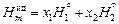 ,
,
где 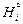 - энтальпия чистого компонента i. Относительные интегральная энтальпия и парциальные энтальпии компонентов в совершенном растворе равны нулю:
- энтальпия чистого компонента i. Относительные интегральная энтальпия и парциальные энтальпии компонентов в совершенном растворе равны нулю:
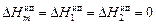 . (1.2)
. (1.2)
Поэтому ненулевые энтальпии – всегда избыточные. Их называют просто энтальпиями (парциальными или интегральными).
Энтропия при образовании совершенного раствора увеличивается, поскольку повышается термодинамическая вероятность, которая характеризуется числом способов реализации данного энергетического состояния системы. (Например, в бинарном идеальном растворе перестановка двух разнородных атомов приводит к новому состоянию раствора, хотя его энергия не изменяется.)
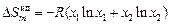 . (1.3)
. (1.3)
Относительная парциальная мольная энтропия компонента совершенного раствора
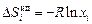 . (1.4)
. (1.4)
Из уравнений (1.2) – (1.4)
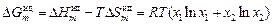 ;
;
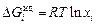 .
.
Относительные парциальная и интегральная энергии Гиббса реального раствора равны:
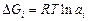 ;
;
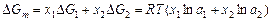 ,
,
где ai - активность компонента i, ai = giх i; gi - коэффициент активности компонента i.
Избыточные термодинамические величины 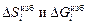 представляют собой разность между соответствующими относительными парциальными или интегральными величинами для реального и идеального растворов:
представляют собой разность между соответствующими относительными парциальными или интегральными величинами для реального и идеального растворов:
избыточная парциальная энергия Гиббса
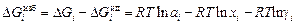 ;
;
избыточная парциальная энтропия
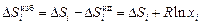 .
.
Аналогично определяют избыточные интегральные термодинамические величины:
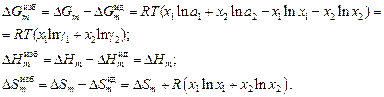 (1.5)
(1.5)
Решение. Рассчитаем избыточные интегральные мольные термодинамические характеристики расплава Fe–Ni эквиатомного состава (xFe = xNi = 0,5). Избыточную энергию Гиббса определяем по уравнению
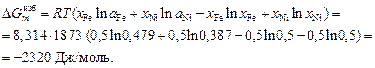
Энтальпия образования расплава равна относительной мольной интегральной энтальпии или просто теплоте образования:
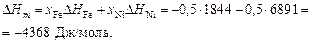
Избыточную энтропию при T = 1873 К вычисляем по уравнению
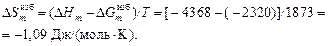
Результаты расчета избыточных термодинамических характеристик расплавов Fe–Ni в зависимости от состава приведены на рисунке.
 Примечания. 1. При gi < 1 (
Примечания. 1. При gi < 1 ( 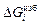 < 0) имеет место отрицательное отклонение от закона Рауля, при gi > 1 (
< 0) имеет место отрицательное отклонение от закона Рауля, при gi > 1 ( 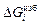 > 0) - положительное отклонение от закона Рауля. Расплавы Fe–Ni характеризуются отрицательным отклонением от закона Рауля.
> 0) - положительное отклонение от закона Рауля. Расплавы Fe–Ni характеризуются отрицательным отклонением от закона Рауля.
2. Были рассмотрены избыточные термодинамические величины относительно совершенного раствора. Моделью идеального раствора может служить также разбавленный раствор, подчиняющийся закону Генри. Отклонения от закона Генри характеризуются коэффициентом активности fi . В этом случае 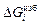 = RTlnfi . Отрицательному отклонению от закона Рауля соответствует положительное отклонение от закона Генри, и наоборот.
= RTlnfi . Отрицательному отклонению от закона Рауля соответствует положительное отклонение от закона Генри, и наоборот.
3. Активность и коэффициент активности
для различных стандартных состояний
Задача. Рассчитать коэффициенты активности титана fTi в расплавах Ni–Тi (стандартное состояние - 1 %-ный раствор) по данным о gTi (стандартное состояние - чистый жидкий титан) при 1800 К.








