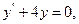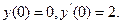Глава 9. Диференціальні рівняння
другого порядку
9.1. Диференціальні рівняння, що допускають знижен-
ня порядку.
Означення. Рівняння вигляду
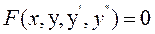 (9.1)
(9.1)
називається диференціальним рівнянням другого порядку.
Рівняння, розв'язане відносно похідної 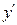 , має вигляд:
, має вигляд:
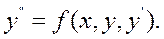 (9.2)
(9.2)
Загальним розв’язком диференціального рівняння другого порядку
називають функцію:
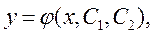 (9.3)
(9.3)
яка залежить від аргументу 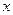 та від двох довільних стали
та від двох довільних стали 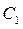 та
та 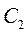 . Якщо визначити функцію
. Якщо визначити функцію 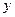 явним способом неможливо, розв’язок, що його отримують у цьому випадку, називають загальним інтегралом диференціального рівняння:
явним способом неможливо, розв’язок, що його отримують у цьому випадку, називають загальним інтегралом диференціального рівняння:
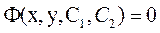 (9.4)
(9.4)
Частинний розв’язок (частинний інтеграл) знаходять із загального
розв'язку при будь -яких значеннях довільних сталих. Якщо до рівняння задаються начальні умови, то частинний розв'язок можна знайти відповідно до цих умов. Начальні умови для рівняння другого порядку будуть
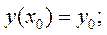
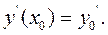 (9.5)
(9.5)
Задача Коші. Знайти частинний розв'язок диференціального рівняння (9..1) 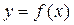 ,що задовольняє начальним умовам (9.5). Отже для знаходження розв'язку задачі Коші треба спочатку знайти загальний розв'язок рівняння (9.3) або (9.4) та визначити сталі
,що задовольняє начальним умовам (9.5). Отже для знаходження розв'язку задачі Коші треба спочатку знайти загальний розв'язок рівняння (9.3) або (9.4) та визначити сталі 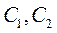 із початкових умов (9.5)
із початкових умов (9.5)
Геометричне тлумачення початкових умов для диференціального рівняння другого порядку полягає в тому, що крім точки 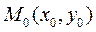 , через яку проходить інтегральна крива, ми задаємо кутовий коефіцієнт дотичної
, через яку проходить інтегральна крива, ми задаємо кутовий коефіцієнт дотичної 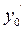 до цієї кривої в точці
до цієї кривої в точці 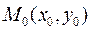 . Оскільки загальний розв’язок диференціального рівняння другого порядку залежить від двох довільних сталих, через дану точку проходить безліч інтегральних кривих, та лише одна з них має даний кутовий коефіцієнт:
. Оскільки загальний розв’язок диференціального рівняння другого порядку залежить від двох довільних сталих, через дану точку проходить безліч інтегральних кривих, та лише одна з них має даний кутовий коефіцієнт:
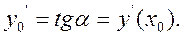
Довільні сталі  та
та 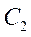 одержують із системи рівнянь:
одержують із системи рівнянь:
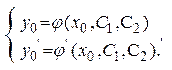 (9.6)
(9.6)
Розглянемо найпростіші випадки диференціальних рівнянь другого
порядку, які припускають зниження порядку.
1. Напростішим рівнянням такого вигляду є рівняння:
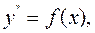
тобто рівняння, права частина якого залежить лише від незалежної змінної 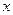 . Зінтегрувавши ліву та праву частини рівняння, одержимо:
. Зінтегрувавши ліву та праву частини рівняння, одержимо:
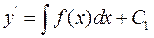
де 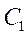 - довільна стала інтегрування. Зінтегрувавши одержаний вираз ще раз, отримаємо загальний розв’язок рівняння:
- довільна стала інтегрування. Зінтегрувавши одержаний вираз ще раз, отримаємо загальний розв’язок рівняння:
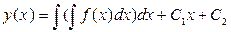 (9.7)
(9.7)
Таким чином, диференціальне рівняння другого порядку має безліч
розв’язків. Як відмічено вище ,щоб знайти частинний розв’язок, необхід-
но задовольнити початковим умовам, тобто визначити довільні сталі 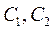
Приклад. 9.1. Розв’язати рівняння: 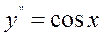
Розв'язання.
Оскільки 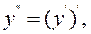 то
то 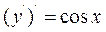 , тобто
, тобто 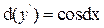 . Зінтегрував-
. Зінтегрував-
ши обидві частини цього рівняння, ми отримаємо:
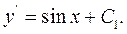
Таким чином, 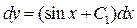 . Зінтегрувавши обидві частини одержаного виразу, ми отримаємо загальний розв’язок початкового рівняння:
. Зінтегрувавши обидві частини одержаного виразу, ми отримаємо загальний розв’язок початкового рівняння:
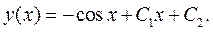
Приклад. 9.2.Знайти частинний розв'язок рівняння 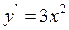 , що за-
, що за-
довольняє початковим умовам 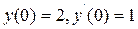 .
.
Розв'язання.
Спочатку шукаємо загальний розв'язок рівняння 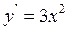 , який має
, який має
вигляд (9.7).Треба послідовно проінтегрувати дане рівняння. Беручи до уваги, що 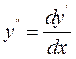 , маємо
, маємо 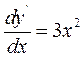 або
або 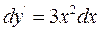 . Беремо інтеграл від обох частин
. Беремо інтеграл від обох частин
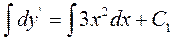 або
або 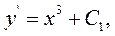 тобто
тобто
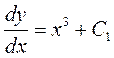
Помножимо на 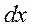 обидві частини рівняння
обидві частини рівняння 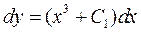 . Інтегруємо
. Інтегруємо
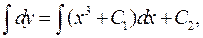
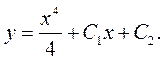
Тепер треба знайти 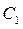 і
і 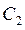 , враховуючи початкові умови. За умовою
, враховуючи початкові умови. За умовою 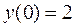 і тоді
і тоді 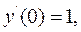 тоді
тоді
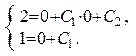
Отже, 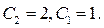 Таким чином, частинний розв'язок
Таким чином, частинний розв'язок
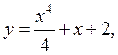 або
або 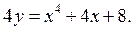
2. Диференціальне рівняння, яке припускає зниження порядку, є рівняння вигляду:
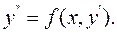 (9.8)
(9.8)
Права частина рівняння не містить в собі невідомої функції. В цьому випадку рівняння може бути розв’язане за допомогою підстановки:
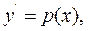
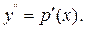 (9.9)
(9.9)
Внаслідок застосування цієї підстановки, рівняння(9..8) набуває вигляду:
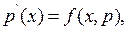 (9.10)
(9.10)
тобто його порядок знижується. Отже маємо диференціальне рівняння
першого порядку.
Приклад 9.3.Розв’язати рівняння: 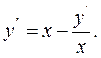
Розв'язання.
Оскільки рівняння не містить в собі невідомої функції 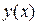 (9.8), для
(9.8), для
його розв’язання використаємо підстановку: 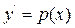 та
та 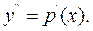
Одержимо лінійне диференціальне рівняння першого порядку:
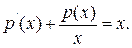
Для його розв'язання зробимо заміну
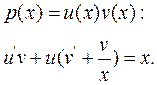
Прирівнявши вираз, що стоїть в останньому рівнянні у дужках, до нуля, ми отримаємо:
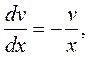 або
або 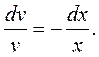
Зінтегрувавши ліву та праву частини останнього співвідношення
отримаємо: 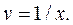 Отже, для знаходження невідомої функції
Отже, для знаходження невідомої функції 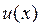 маємо диференціальне рівняння:
маємо диференціальне рівняння:
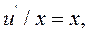 тобто
тобто 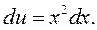
Ми визначили, що функція 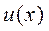 дорівнює:
дорівнює: 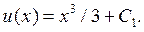
Тепер знайдемо функцію 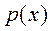 :
:
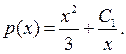
Оскільки 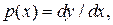 звідси маємо:
звідси маємо:
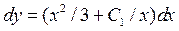
Зінтегрувавши обидві частини останнього рівняння, отримаємо остаточний розв’язок початкового рівняння:
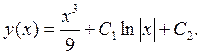
Приклад 9.4.Знайти загальний розв'язок рівняння 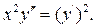
Розв'язання.
Маємо рівняння вигляду (9.8), тому застосовуємо заміну 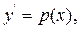
звідки 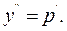 Після цього дане рівняння приймає вигляд
Після цього дане рівняння приймає вигляд 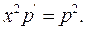
Отримали рівняння з відокремлюваними змінними
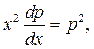 або
або 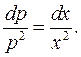
Беремо інтеграл від обох частин
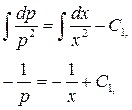 або
або 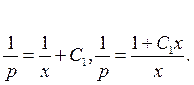
Звідки
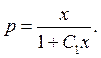
Враховуючи, що 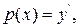 маємо
маємо
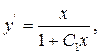 або
або 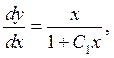 отже
отже 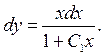
Інтегруємо обидві частини останньої рівності
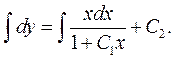
Для знаходження 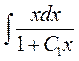 треба виділити цілу частину, бо підінтегральна функція є неправильний раціональний дріб. Для цього треба поділити чисельник на знаменник.
треба виділити цілу частину, бо підінтегральна функція є неправильний раціональний дріб. Для цього треба поділити чисельник на знаменник.
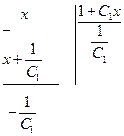
Інтеграл приймає вигляд
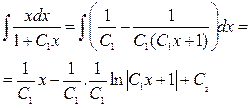
Таким чином,
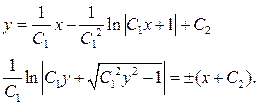
3. Рівняння, яке не містить явно аргументу.
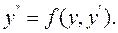 (9.11)
(9.11)
Права частина рівняння у цьому разі не містить в собі незалежної
змінної 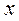 , і розв’язок можна одержати за допомогою підстановки:
, і розв’язок можна одержати за допомогою підстановки:
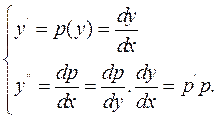 (9.12)
(9.12)
Підставляючи невідому функцію 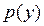 та її похідну
та її похідну 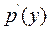 у початкове рівняння (9.11) отримаємо диференціальне рівняння першого порядку відносно
у початкове рівняння (9.11) отримаємо диференціальне рівняння першого порядку відносно 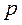 , як функції від
, як функції від 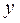 :
:
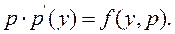 (9.13)
(9.13)
Приклад 9.5. Розв’язати рівняння:
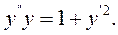
Розв'язання.
Позначивши 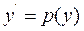 та
та 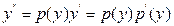 і підставивши ці вирази у початкове рівняння, одержимо:
і підставивши ці вирази у початкове рівняння, одержимо: 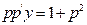 – диференціальне рівняння із відокремлюваними змінними. Відокремивши змінні, отримаємо:
– диференціальне рівняння із відокремлюваними змінними. Відокремивши змінні, отримаємо:
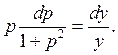
Звідси:
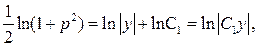
або
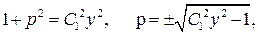
або
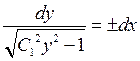
Зінтегрувавши обидві частини одержаного рівняння, отримаємо загальний інтеграл початкового диференціального рівняння:
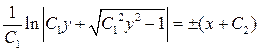
9.2. Однорідне лінійне диференціальне рівняння другого порядку із сталими коефіцієнтами.
Означення. Лінійним однорідним диференціальним рівнянням n n -
го порядку із сталими коефіцієнтами називається рівняння вигляду
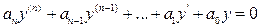 (9.14)
(9.14)
де 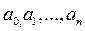 - дійсні числа. Частинним випадком рівняння є рівняння другого порядку
- дійсні числа. Частинним випадком рівняння є рівняння другого порядку
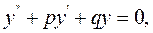 (9.15)
(9.15)
де коефіцієнти 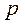 та
та 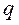 – сталі.
– сталі.
Розглянемо властивості розв'язку рівняння (9.15) і зупинимось на різних випадках знаходження його розв'язків.
Теорема 1. Якщо 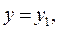 є розв'язком рівняння
є розв'язком рівняння 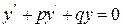 , то і
, то і
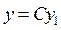 , де
, де 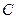 – вільна стала, теж буде розв'язком цього рівняння.
– вільна стала, теж буде розв'язком цього рівняння.
Доведення.
За умовою теореми
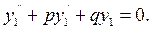
Тепер підставимо в рівняння (9.15) 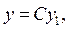 одержимо:
одержимо:
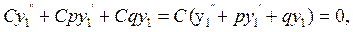
а це і означає,що 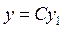 також є розв'язком рівняння ()
також є розв'язком рівняння ()
Теорема 2. Якщо 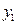 òà
òà 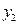 – розв'язки рівняння
– розв'язки рівняння 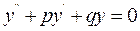 то їх
то їх
сума теж є розв'язком цього рівняння.
Доведення.
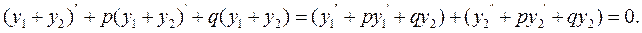
Тобто, сума 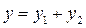 також є розв'язком рівняння.
також є розв'язком рівняння.
Означення . Два розв'язки, 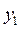 òà
òà 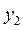 , називаються лінійно незалежними на множині
, називаються лінійно незалежними на множині 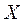 , якщо їх відношення не дорівнює сталому числу. У протилежному випадку розв'язки
, якщо їх відношення не дорівнює сталому числу. У протилежному випадку розв'язки 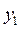 òà
òà 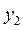 називаються лінійно залежними.
називаються лінійно залежними.
Теорема 3. Якщо 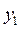 òà
òà 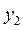 – незалежні розв'язки рівняння
– незалежні розв'язки рівняння
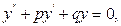 то
то 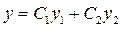 є загальний розв'язок цього рівняння.
є загальний розв'язок цього рівняння.
Доведення.
Відповідно до теорем 1 та 2 випливає, що 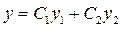 є розв'язком рівняння (9.15) і цей розв'язок залежить від двох вільних сталих
є розв'язком рівняння (9.15) і цей розв'язок залежить від двох вільних сталих
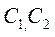 .
.
Теорема 4. Якщо розв'язки рівняння 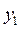 та
та 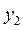 лінійно залежні, то
лінійно залежні, то
розв'язок 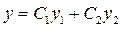 не буде загальним розв'язком рівняння (9.15).
не буде загальним розв'язком рівняння (9.15).
Дійсно, якщо 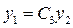 ,то
,то
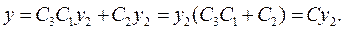
Розв'язок 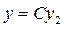 є частинним розв'язком рівняння,тому що залежить від однієї вільної сталої C . Таким чином, із теореми 3 можна зробити висновок: щоб знайти загальний розв'язок рівняння (9.15 ) , треба знайти два його лінійно незалежних розв'язки
є частинним розв'язком рівняння,тому що залежить від однієї вільної сталої C . Таким чином, із теореми 3 можна зробити висновок: щоб знайти загальний розв'язок рівняння (9.15 ) , треба знайти два його лінійно незалежних розв'язки 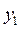 та
та 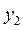 і тоді
і тоді 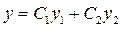 буде загальним розв'язком цього рівняння.
буде загальним розв'язком цього рівняння.
9.3. Знаходження загального розв'язку однорідного
диференціального рівняння другого порядку
Будемо шукати частинний розв’язок рівняння
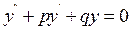
у вигляді показникової функції
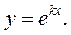
Підставивши у рівняння першу та другу похідні частинного
розв’язку, та маючи на увазі, що 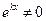 , після спрощення отримаємо рівняння:
, після спрощення отримаємо рівняння:
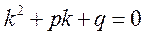 (9.16)
(9.16)
Це рівняння відносно k називається характеристичним рівнянням
даного однорідного лінійного диференціального рівняння другого порядку із сталими коефіцієнтами.
Зауважимо, що для того, щоб одержати характеристичне рівняння,
достатньо похідні 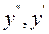 та функцію y замінити на відповідні степені величини
та функцію y замінити на відповідні степені величини 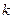 , розглядаючи при цьому функцію y як похідну нульового порядку.
, розглядаючи при цьому функцію y як похідну нульового порядку.
Розв’язавши характеристичне рівняння, знайдемо значення 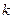 :
:
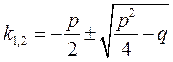 (9.17)
(9.17)
Розглянемо різні випадки розв’язків характеристичного рівняння,
від яких залежить вигляд частинного розв’язку:
1. Якщо 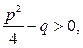 , корені рівняння дійсні та різні:
, корені рівняння дійсні та різні: 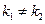 . У цьому
. У цьому
випадку 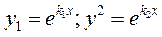 – лінійно незалежні розв’язки рівняння. Частинні розв’язки рівняння
– лінійно незалежні розв’язки рівняння. Частинні розв’язки рівняння 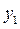 і
і 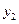 лінійно незалежні, і тому що їх співвідношення не є сталою величиною. Тоді відповідно теоремі 3 загальний розв'язок рівняння буде
лінійно незалежні, і тому що їх співвідношення не є сталою величиною. Тоді відповідно теоремі 3 загальний розв'язок рівняння буде
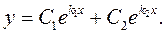 (9.18)
(9.18)
Приклад. 9.6. Знайти загальний розв’язок диференціального рівняння:
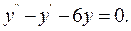
Складемо характеристичне рівняння: 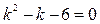 . Це рівняння має
. Це рівняння має
різні дійсні корені: 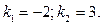 . Їм відповідають два частинних розв’язки:
. Їм відповідають два частинних розв’язки: 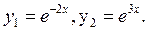
Отже, загальний розв’язок рівняння має вигляд:
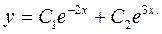
2. Якщо 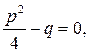 то корені характеристичного рівняння дійсні та рівні:
то корені характеристичного рівняння дійсні та рівні: 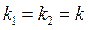 У цьому випадку
У цьому випадку 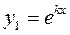 – частинний розв’язок рівняння. Другий частинний розв'язок знайдемо у вигляд
– частинний розв’язок рівняння. Другий частинний розв'язок знайдемо у вигляд 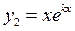
Тоді відповідно теоремі 3 загальний розв'язок рівняння буде
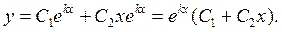
Приклад. 9.7.Знайти загальний розв’язок рівняння: 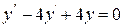 .
.
Запишемо характеристичне рівняння цього диференціального рівняння: 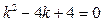 . Його корені:
. Його корені: 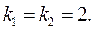 . Тобто рівняння має один двократний дійсний корінь. Йому відповідають два частинних розв’язка рівняння:
. Тобто рівняння має один двократний дійсний корінь. Йому відповідають два частинних розв’язка рівняння: 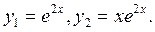
Загальний розв’язок рівняння має вигляд:
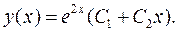
3. Якщо 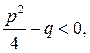 , рівняння має комплексно- спряжені корені:
, рівняння має комплексно- спряжені корені:
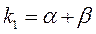 ;
; 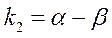
де
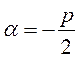 ;
; 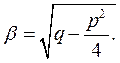
У цьому випадку частинні розв’язки рівняння мають вигляд:
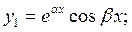
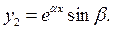
Тоді відповідно теоремі 3 загальний розв'зок рівняння буде
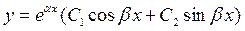 (9.20)
(9.20)
Приклад. 9.8. Знайти загальний розв’язок рівняння:
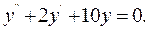
Розв'язання.
Запишемо характеристичне рівняння: 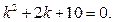 Воно має
Воно має
комплексні корені: 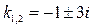 . Тобто
. Тобто 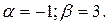 . Цим кореням відповідають два частинних розв’язка:
. Цим кореням відповідають два частинних розв’язка:
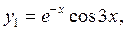 та
та 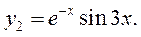
Загальний розв’язок рівняння має вигляд:
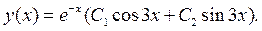
Запитання для самодіагностики
1. Які диференціальні рівняння другого порядку допускають зниження порядку?
2. Як розв’язати рівняння 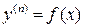 ?
?
3. Як розв’язати рівняння 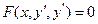 ?
?
4. Як розв’язати рівняння 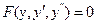 ?
?
5. Що називається лінійним диференціальним рівнянням другого
порядку?
6. Яке рівняння називається однорідним?
7. Які функції називаються лінійно незалежними?
8. Який вигляд має лінійне однорідне диференціальне рівняння
другого порядку із сталими коефіцієнтами?
9. Як складається характеристичне рівняння?
9. Як записати загальний розв'язок однорідного рівняння, коли
а) корені характеристичного рівняння дійсні і різні;
б) корені характеристичного рівняння дійсні і рівні;
в) корені характеристичного рівняння комплексні.
Приклади і вправи
Приклади.
Розв’язати рівняння, що припускають зниження порядку
9.9 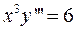
Розв'язання.
Запишемо задане рівняння у вигляді 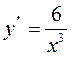 Послідовно інтегруючи це рівняння, одержуємо
Послідовно інтегруючи це рівняння, одержуємо
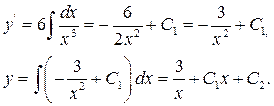
Загальний розв'язок рівняння – 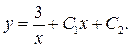
9.10. 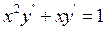
Розв'язання.
Рівняння не містить функцію 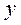 . Тому зробимо підстановку
. Тому зробимо підстановку
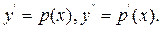 . Одержимо рівняння
. Одержимо рівняння
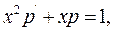 або
або 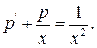
Це лінійне рівняння першого порядку. Його розв'язок шукаємо у вигляді 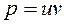 , звідки
, звідки 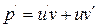 .
.
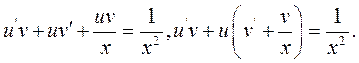
З рівняння 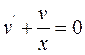 знаходимо
знаходимо 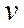 :
:
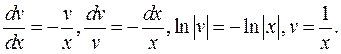
Далі знаходимо 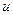 з рівняння
з рівняння 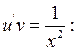
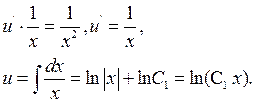
Тоді 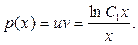 Але
Але 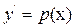 , тобто
, тобто
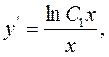 а
а 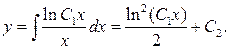
Загальний розв'язок – 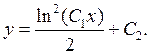
9.11. 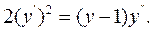
Розв'язання.
Рівняння не містить незалежної змінної 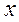 . Тому робимо підстановку
. Тому робимо підстановку
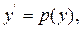 а
а 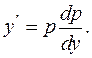
Задане рівняння приймає вигляд
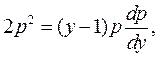 або
або 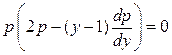 .
.
Звідки маємо 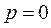 , або
, або 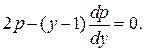
З першого рівняння 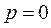 ,
, 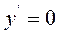 , одержуємо
, одержуємо 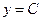 . В другому
. В другому
рівнянні поділимо змінні і знайдемо його загальний розв'язок:
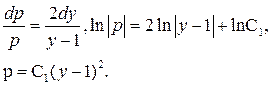
Підставляючи в останнє рівняння обернену змінну 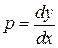 , одержуємо знову рівняння першого порядку
, одержуємо знову рівняння першого порядку
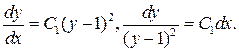
Проінтегруємо:
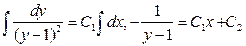
Або
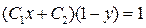 – це загальний інтеграл рівняння.
– це загальний інтеграл рівняння.
9.12.Знайти частинний розв'язок рівняння
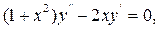
що задовольняє початкові умови 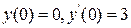
Розв'язання.
Після заміни 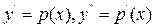 одержуємо рівняння першого по-
одержуємо рівняння першого по-
рядку з подільними змінними:
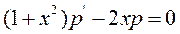 або
або 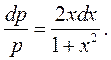
Звідси: 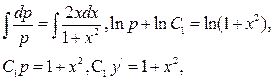
а тоді,
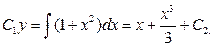
Знайдемо 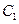 і
і 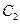 застосовуючи початкові умови:
застосовуючи початкові умови: 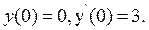 . Отже
. Отже
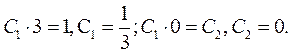
Частинний розв'язок 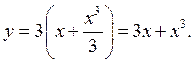
Розв'язати лінійні однорідні рівняння другого порядку:
9.13. Знайти загальний розв'язок рівнянь:
а) 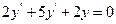 ; б)
; б) 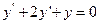 ;
;
в) 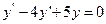 .
.
Розв'язання.
Для кожного з рівнянь складаємо характеристичне рівняння.
a) 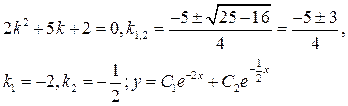
б) 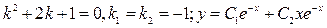
в) 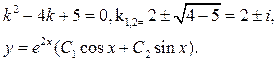
9.14. Знайти частинний розв'язок рівняння
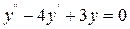
який задовольняє початкові умови 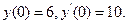
Розв'язання.
Корені характеристичного рівняння 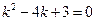 мають значення
мають значення
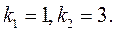 Загальний розв'язок рівняння
Загальний розв'язок рівняння
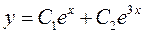
Знайдемо 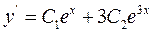 . Для визначення частинного розв'язку
. Для визначення частинного розв'язку
використовуємо початкові умови 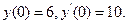 . Одержуємо систему
. Одержуємо систему
рівнянь:
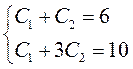 звідси
звідси 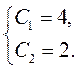
Частинний розв'язок має вигляд
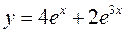
Вправи.
Розв’язати рівняння.
9.15 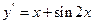 9.16
9.16 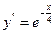
9.17 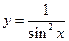 9.18
9.18 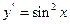
9.19 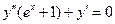 9.20
9.20 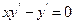
9.21 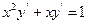 9.22
9.22 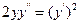
9.23 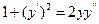 9.24
9.24 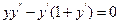
Знайти частинні розв'язки, які задовольняють вказані початкові умови.
9.25 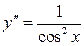 ,
, 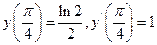
9.26 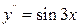 ,
, 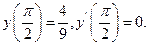
9.27 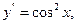
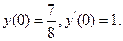
9.28 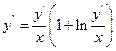
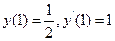
9.29 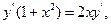
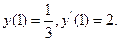
9.30 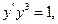
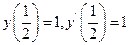
9.31 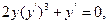
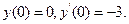
Знайти загальні розв'язки рівнянь.
9.32 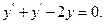 9.33
9.33 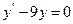
9.34 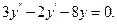 9.35
9.35 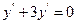
9.36 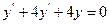 9.37
9.37 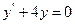
9.38 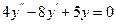 9.39
9.39 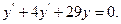
9.40 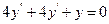 9.41
9.41 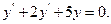
Знайти частинні розв'язки рівнянь при вказаних початкових умовах
9.42 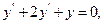
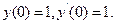
9.43 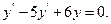
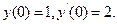
9.44 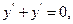
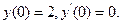
9.45 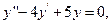
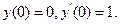
9.46 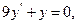
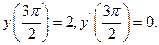
9.47 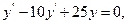
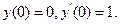
9.48 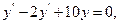
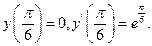
9.49