Элементарные свойства вероятности
МАТЕРИАЛЫ
ДЛЯ СТУДЕНТОВ ЗАОЧНОГО ОТДЕЛЕНИЯ
СПбГЭТУ (ЛЭТИ)
Курс «Теория вероятностей и математическая статистика»
Кафедра ВМ-2
Курс 3
Семестр 5
Санкт-Петербург
2009 г.
1. ПРОГРАММА КУРСА.
ЭЛЕМЕНТАРНЫЕ СВОЙСТВА ВЕРОЯТНОСТИ
Элементы комбинаторики. Классическое и геометрическое определения вероятности. Действия над событиями. Основные свойства вероятности. Условная вероятность, независимость событий. Формулы полной вероятности и Байеса. Схема Бернулли, предельные теоремы для схемы Бернулли: теорема Пуассона и теоремы Муавра-Лапласа.
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Аксиомы теории вероятностей. Случайные величины. Дискретные и абсолютно непрерывные случайные величины. Примеры: случайные величины, имеющие биномиальное, пуассоновское, равномерное, показательное, нормальное распределения. Числовые характеристики случайных величин. Вычисление их для классических распределений: распределения Бернулли, биномиального, пуассоновского, равномерного для конечной совокупности, равномерного, показательного, нормального. Случайные векторы и их распределения. Независимость случайных величин. Нормальный случайный вектор. Вектор, имеющий равномерное распределение в ограниченной области. Вычисление распределений одномерных компонент случайных векторов. Неравенство Чебышева. Закон больших чисел. Центральная предельная теорема. Коэффициент корреляции. Условные распределения и условные математические ожидания.
Математическая статистика
Общая статистическая модель. Выборка. Выборочные характеристики: выборочное математическое ожидание, выборочная дисперсия, выборочные моменты, выборочная медиана. Выборочный подход к построению оценок. Примеры. Другие методы нахождения оценок: метод моментов, метод максимального правдоподобия, оценки метода наименьших квадратов. Основные требования к оценкам: состоятельность, несмещенность. Общие понятия эффективности оценок.
Доверительные интервалы. Примеры: Доверительный интервал для математического ожидания нормальной выборки при известной и неизвестной дисперсии. Доверительный интервал для дисперсии при известном и неизвестном математическом ожидании.
Проверка простых гипотез. Критерии Стьюдента. Примеры. Непараметрические критерии: критерий Колмогорова и критерий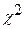 
(хи-квадрат). Критерий 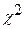при наличии мешающих параметров.
Техника использования различных статистических таблиц.