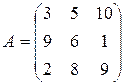Решение антагонистических игр m´n. Сведение матричной игры к задаче линейного программирования
Пусть дана игра m´n в нормальной форме, т.е.
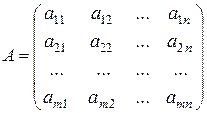
Будем считать, что все элементы матрицы больше 0. Если это не так, то ко всем элементам можно прибавить такое число L>0, например,
,
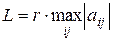где r > 1, чтобы все элементы стали положительными. При этом цена игры возрастает на L, но оптимальные стратегии не меняются. Т.о. aij >0, значит, v > 0
Пусть игрок А применит свою оптимальную стратегию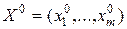 
. Тогда его выигрыш будет не менее v при любых действиях игрока В. В частности, если игрок В применит свою чистую стратегию В j, то выигрыш А составит:
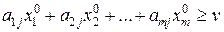j = (1, …, n)
Поделим это неравенство на v и, обозначив
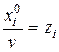(i = 1, …, m),
получим:
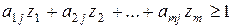zi >= 0 j = (1, …, n)
Вероятности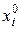 
(i = 1, …, m) должны удовлетворять условию
.
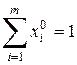Поделим это выражение на v и в новых обозначениях запишем
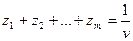
Поскольку игрок А стремиться к максимуму v, то целевая функция будет иметь вид:
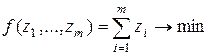
Т.о. имеем:
(1) 
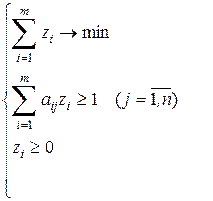
Задача (1) – задача линейного программирования.
Пусть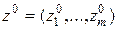 
– решение задачи (1).
Тогда
; 
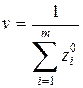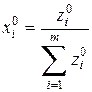(i = 1, …, m).
Аналогичные рассуждения можно проделать для игрока В:
Пусть он применяет оптимальную смешанную стратегию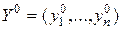 
, а игрок А – чистую стратегию А i (i = 1, …, m). Тогда проигрыш игрока В составит величину не более v:
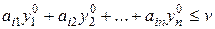(i = 1, …, m).
Разделим это неравенство на v > 0 и, обозначив
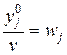(j = 1, …, n), получим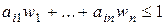 
.
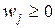Вероятности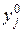 
(i = 1, …, m) должны удовлетворять условию
.
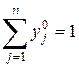Поделим это выражение на v и в новых обозначениях получим:
.
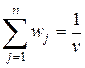Поскольку игрок В стремиться минимизировать проигрыш, т.е.
v ® min,
получим функцию
.
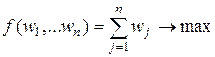Т.о. имеем задачу линейного программирования:
(2) 
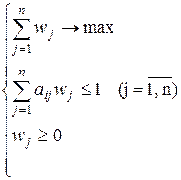
Пусть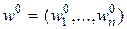 
– решение (2).
Тогда
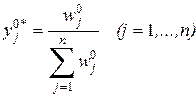
Легко видеть, что задачи (1) и (2) представляют собой пару взаимодвойственных задач линейного программирования. Т.о., решение антагонистической игры m´n можно найти путем решения пары взаимодвойственных задач линейного программирования.
Пример
Две отрасли могут осуществлять капитальные вложения в 3 объекта. Стратегии отраслей: i-я стратегия состоит в финансировании i-го объекта (i = 1, 2, 3). Учитывая особенности вкладов и местные условия, прибыли первой отрасли выражаются следующей матрицей:
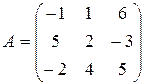
Величина прибыли первой отрасли считается такой же величиной убытка для второй отрасли - представленная игра может рассматриваться как игра двух игроков с нулевой суммой.
Рассмотрим игрока А. Будем искать оптимальную смешанную стратегию игрока А: Х ( х1, х2, х3), где х i – частота (вероятность) использования игроком А своей i-стратегии ( i = 1, 2, 3).Обозначим цену игры (средний выигрыш) – v.
Чтобы свести матричную игру для игрока А к задаче линейного программирования преобразуем платежную матрицу так, чтобы все ее элементы были больше нуля – прибавим ко всем элементам матрицы число 4. Получаем преобразованную платежную матрицу:
