Решение антагонистических игр m×2
Найдем решение игры со следующей матрицей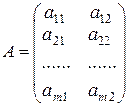 
Пусть игрок В применяет смешанную стратегию Y = (у, (1 – у)), а игрок А – чистую стратегию Ai (i = 1, …, m). Тогда средний проигрыш игрока В будет:
Z = ai1×у + ai2×(1 – у)
Это уравнение прямой, которую обозначим Ai.
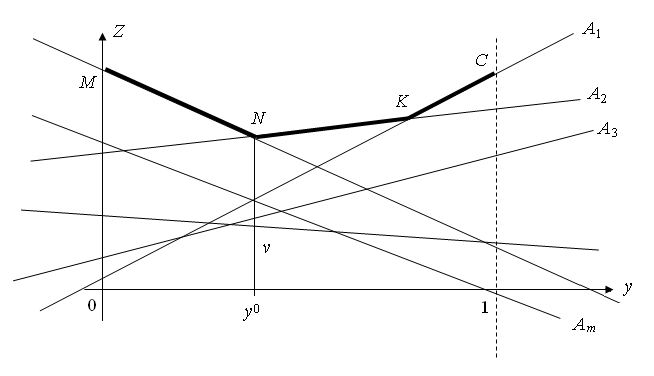
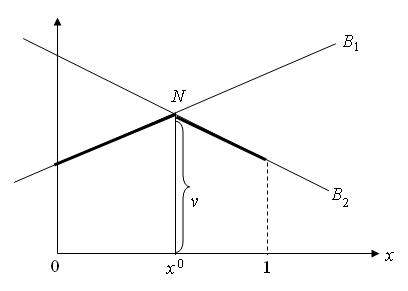
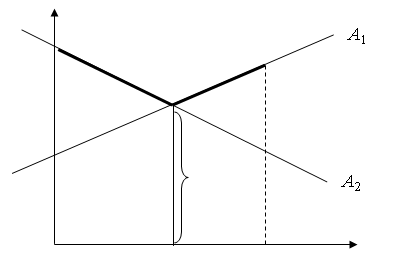
Для i = 1, …, m, построим все прямые А1, А2, …, А m. Проигрыш игрока В будет не больше максимального значения ординат прямых А1, А2, …, А m, т.е. не больше ординат ломаной MNKC. Оптимальной стратегией игрока В будет такая смешанная стратегия, при которой его максимально возможный проигрыш будет минимальным, т.е. будет минимальна ордината ломаной MNKC. Это точка у0, и оптимальная стратегия (у0, (1 – у0)). Цена игры – ордината точки N.
В качестве активных стратегий игрока А можно выбрать две чистых стратегии, соответствующие прямым, пересекающимся в N. Пусть это Ai и Aj.
Из матрицы исходной игры вычеркнем все строки кроме i-ой и j-ой, т.е. получим матрицу:
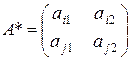
Тогда оптимальную смешанную стратегию игрока А X0 = (х0, (1 – х0) ) можно определить как для игры 2´2, т.е. из соотношений
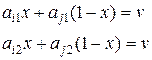
Тогда: Х0 = (0, …, 0, х0, 0, …, 0, 1 – х0, 0, …, 0)
i-я компонента j-я компонента
Пример 1:
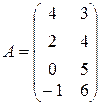
А1 : 4y + 3 (1 – y) = z
A2 : 2y + 4 (1 – y) = z
A3 : 5 (1 – y) = z
A4 : –y + 6 (1 – y) = z
В точке N пересекаются прямые А1 и А4, т.е.
4y + 3 (1 – y) = –y + 6 (1 – y)
y0 = 3/8, Y 0 = (3/8, 5/8)
v = 4×3/8 + 3×(1 – 3/8) = 27/8
Поскольку активными стратегиями А являются А1 и А4, то
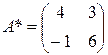
Отсюда получаем В1 : 4x0 – (1 – x0) = z0 = v
В2 : 3x0 + 6 (1 – x0) = z0 = v
Или 4x0 – (1 – x0) = 3x* + 6 (1 – x0)
x0 = 7/8, 1 – x0 = 1/8
Тогда Х 0 = (7/8, 0, 0, 1/8).
Решение антагонистических игр 2× n
Рассмотрим матрицу игры 2×n:
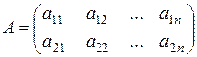
Пусть игрок А применяет смешанную стратегию (х, 1–х), а игрок В – активную стратегию Bj (j = 1, …, n).
В i : z = a1i x + a2i (1 – x)
Изобразим прямые В1, …, Вn на плоскости. Какую бы стратегию ни применил игрок В, игрок А получит выигрыш не менее ординаты ломаной линии MNKC.
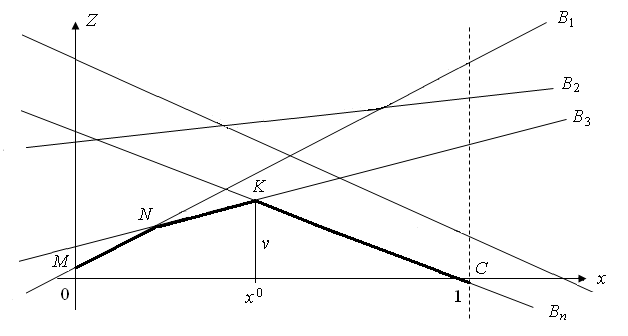
Оптимальная смешанная стратегия первого игрока есть такая смешанная стратегия, при которой он получает максимальный гарантированный выигрыш. На рис. это точка х0, которая соответствует max из ординат ломаной MNKC. Поэтому оптимальная стратегия игрока А:
Х0 = (x0, (1 – x0)),
а цена игры v равна ординате точки К. В качестве активных стратегий игрока В можно выбрать две чистых стратегии, соответствующих любым двум прямым, пересекающимся в точке К. Пусть это Вi и Вj. Тогда матрицу исходной игры можно записать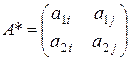 
Оптимальную смешанную стратегию игрока В найти как в игре 2´2
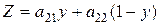
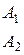
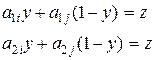
Тогда: Y 0 = (0, …, 0, у0, 0, …, 0, 1 – у0, 0, …, 0)
i-я компонента j-я компонента
Пример 2:
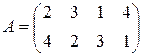
В1 : 2x + 4 (1 – x) = z
В2 : 3x + 2 (1 – x) = z
В3 : x + 3 (1 – x) = z
В4 : 4x + (1 – x) = z
В точке N пересекаются прямые В3 и В4, т.е. x + 3 (1 – x) = 4x + (1 – x), т.е.
x0 = 2/5, Х 0 = (2/5, 3/5)
v = 2/5 + 3 × 3/5 = 11/5
Активными стратегиями игрока В будут В3 и В4, т.е.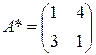 
Тогда А1 : y + 4 (1 – y) = z
A2 : 3y + (1 – y) = z
y0 = 3/5 Y 0 = (0, 0, 3/5, 2/5)
Пример 1.
Решить графическим методом игру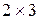 
.
.
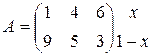Пусть первый игрок придерживается смешанной стратегии
,
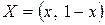а второй игрок – одной из своих чистых стратегий.
Тогда
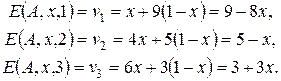
Построим прямые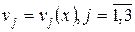 
, определяющие график функции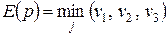 
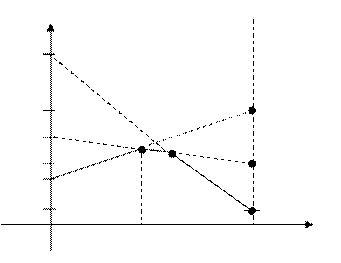
В точке максимума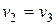 
, т.е.
,
.
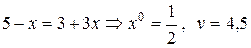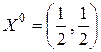Активными стратегиями второго игрока являются вторая и третья стратегии, поэтому оптимальную стратегию этого игрока ищем в виде
.
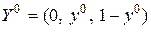Для этого решим игру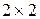 
с матрицей
.
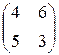По формуле (***) имеем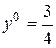 
.
Итак,
.
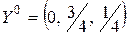Пример 2
Решить игру, заданную платёжной матрицей.
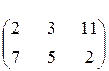
Ответ: Х = (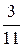 
; 
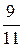), при цене игры v = 
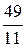. Y = (0; ; 
).
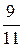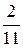Пример 3 . Найти решение игры, заданной матрицей
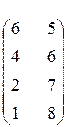
Ответ: U = (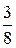 
; 
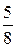); Х = ( 
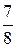; 0; 0; 
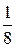); u = 
.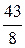