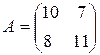Решение антагонистических игр 2×2 в смешанных стратегиях
Если игра 2×2 имеет седловую точку, то ее решение очевидно.
Пусть игра 2×2 не имеет седловой точки. Требуется найти цену игры v и оптимальные смешанные стратегии обоих игроков:
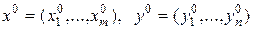 .
.
Чистые стратегии, входящие в оптимальную стратегию с положительными вероятностями, называются активными стратегиями.
Для решения матричных игр 2´2 можно использовать аналитический и геометрический методы.
Аналитический метод
Теорема об активных стратегиях
Пусть v – цена игры, 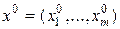 и
и 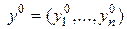 – оптимальные стратегии игроков. Тогда справедливы следующие утверждения:
– оптимальные стратегии игроков. Тогда справедливы следующие утверждения:
– для любой активной стратегии i первого игрока выполняется равенство
E(i, y0) = v;
– для любой активной стратегии j второго игрока имеет место равенство
E(x0, j) = v.
В игре 2×2 все стратегии игроков являются активными (почему?)
Выигрыш игрока первого игрока, если он применяет оптимальную стратегию х0, а второй игрок свою активную стратегию 1 равен
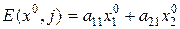
По теореме об активных стратегиях этот выигрыш равен цене игры, т.е.
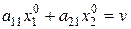
Аналогично для случая, когда первый игрок применяет оптимальную стратегию х0, а второй игрок активную стратегию 2:
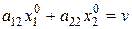
Получаем:
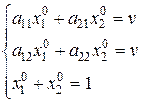 (1)
(1)
Получили систему уравнений относительно 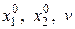 .
.
Аналогичную систему получим для оптимальных стратегий второго игрока:
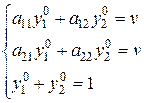 (2)
(2)
Решая эти системы, найдем неизвестные оптимальные стратегии игроков х0, у0 и цену игры v.
Цена игры ν общая для обоих игроков, поэтому при решении систем уравнений (1) и (2) должно получиться одинаковое значение ν.
Решение игры 2´2 в общем виде выглядит следующим образом
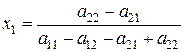 ; х2 = 1 – х1;
; х2 = 1 – х1;
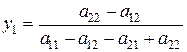 ; у2 = 1 – у1; (***)
; у2 = 1 – у1; (***)
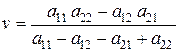 .
.
Геометрический метод
Рассмотрим геометрическую интерпретацию игры 2×2.
Пусть игрок А применяет смешанную стратегию, а игрок В – активную стратегию В1. Тогда средний выигрыш игрока А будет: 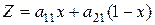
Мы получили уравнение прямой, которую обозначим В1, т.к. она соответствует активной стратегии В1 игрока В.
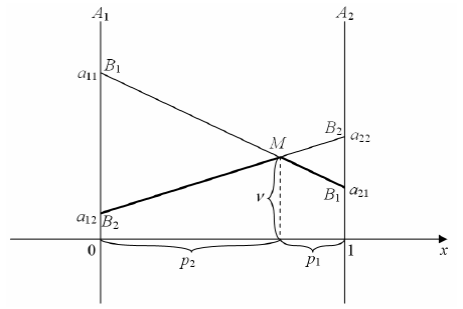
Если игрок В применяет свою активную стратегию В2, а игрок А стратегию (х, (1 – х)), то выигрыш игрока А равен:
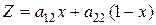
Видно, что какую бы стратегию ни применил В, игрок А гарантирует себе выигрыш не меньше, чем ордината ломаной В2МВ1.
Ломанная В2МВ1 (на рис. выделена полужирно) определяет минимальные возможные средние выигрыши игрока А при использовании им своих смешанных стратегий. Точка М (самая высокая точка ломанной) – определяет наилучший средний выигрыш игрока А из всех минимальных. Она соответствует оптимальной смешанной стратегии игрока А. При этом: если М имеет координаты (х, у), то р1 = 1 – х, р2 = х, ν = y.
Таким образом, задача сводится к нахождению координат точки М, которая является точкой пересечения прямых В1В1 и В2В2. Для нахождения уравнений прямых В1В1 и В2В2.можно воспользоваться уравнением прямой, проходящей через две точки:
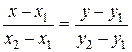 ,
,
с учетом того, что прямую В1В1 определяют точки (0; a11), (1; а21), а прямую В2В2 определяют точки (0; a12), (1; а22).
Для игрока В оптимальная смешанная стратегия находится аналогично, но точка М определяется не самой высокой точкой нижней ломанной, а самой низкой точкой высокой ломанной – полужирная ломанная на рисунке 2.
Пусть В применяет стратегию Y = (у, (1 – у)), а А применяет стратегию А1. Тогда проигрыш игрока В определяется точками прямой:
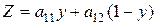 .
.
Эту прямую обозначим А1. Если А применяет стратегию А2, а В стратегию Y, то проигрыш В лежит на прямой А2:
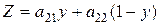
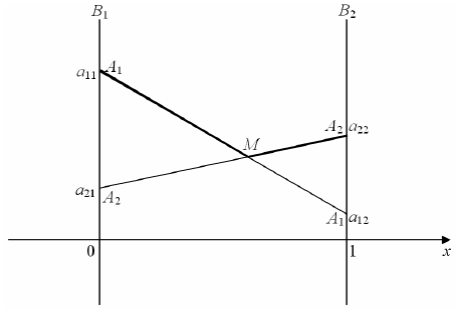
Из графика видно, что какую бы стратегию ни применял игрок А, игрок В гарантирует себе проигрыш не более, чем ордината ломаной А1МА2.
Оптимальной стратегией игрока В будет такая стратегия Y = (у, (1 – у)), при которой ордината ломаной линии А1МА2 будет минимальна. Найдя координаты точки М (х, у), как точки пересечения прямых А1А1 и А2А2, компоненты оптимальной смешанной стратегии игрока В и цену игры: Y*(у1, у2), ν можно найти по следующим формулам:
q1 = 1 – x, q2 = x, ν = y.
Пример.
Решить игру с матрицей платежей 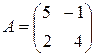
Пусть оптимальная смешанная стратегия игрока А есть 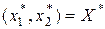 .
.
Тогда:
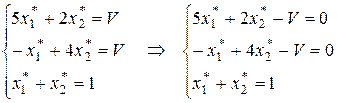
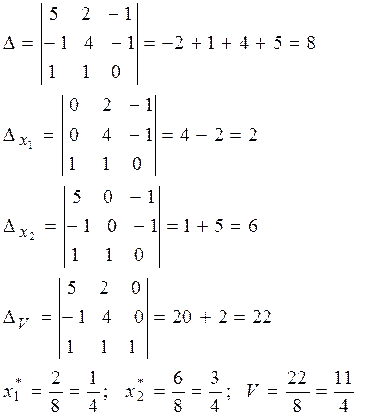
Найдем оптимальную смешанную стратегию 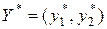 игрока В.
игрока В.
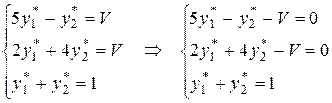
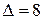

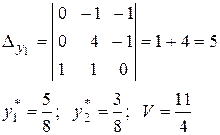

Игру можно решить графически.
Пример.
Решить графически игру с матрицей А