Перед тем, как решать игру m´n, нужно, прежде всего попытаться ее упростить, избавившись от лишних стратегий.
Часто при нахождении решения матричной игры существенно помогает выявление превосходства одной стратегии над другой.
Определение.
Если для i-й и k-й стратегий первого игрока выполняются соотношения
aij ³ akj (j = 1, 2, …, n),
причем хотя бы одно из неравенств является строгим, то говорят, что стратегия i превосходит или доминирует стратегию k.
Аналогично для второго игрока: стратегия j доминирует стратегию r, если выполняются неравенства
aij ³ air (i = 1, 2, …, m),
причем хотя бы одно из неравенств является строгим неравенством.
Использование соотношения доминирования позволяет сократить размерность матрицы выигрышей в матричной игре. Это свойство формулируется в виде следующей теоремы.
Теорема 1.
Пусть Г – матричная игра с матрицей А порядка m´n, и i-я стратегия первого игрока доминирует k-ю стратегию. Пусть А1 матрица, получаемая из А путем исключения из нее k-й строки, и пусть Г1 – матричная игра с матрицей А1.
Тогда цена игры Г1 совпадает с ценой игры Г, всякая оптимальная смешанная стратегия второго игрока в Г1 есть также его оптимальная смешанная стратегия в игре Г, если u = (u1, u2, …, uk–1, uk+1, …, um) есть оптимальная смешанная стратегия первого игрока в игре Г1, то его смешанная стратегия х = (u1, u2, …, uk–1, 0, uk+1, …, um) является оптимальной в игре Г.
Из теоремы следует, что если i-я стратегия первого игрока доминирует k-ю стратегию, то i-я стратегия для первого игрока лучше, чем k-я , т.е. первому игроку не выгодно использовать свою k-ю стратегию и она не должна входить в его оптимальную стратегию. Следовательно, вероятность применения k-й чистой стратегии в оптимальной смешанной стратегии первого игрока должна равняться нулю. Вычеркивая из А эту k-ю строку, получаем матрицу А1, в которой количество строк на единицу меньше. При этом полагаем xk = 0, где xk – k-я компонента х. Игру с матрицей А1 решать легче, так как в ней меньше строк. Если в матрице А1 наблюдается доминирование стратегий первого игрока, то далее можно поступать аналогично и таким образом уменьшить размерность матрицы А1.
Доминирование стратегий для второго игрока также дает дополнительные возможности для сокращения размера матрицы выигрышей.
С этой целью можно использовать следующее свойство.
Теорема 2.
Пусть Г матричная игра с матрицей А. Пусть q-я чистая стратегия второго игрока доминирует r-ю, матрица А1 получена из А исключением q-го столбца, Г1 – матричная игра с матрицей А1. Тогда цена игры Г1 такая же, как цена игры Г; всякая оптимальная смешанная стратегия первого игрока в Г1 есть также его оптимальная смешанная стратегия в Г; если w = (w1, w2, ..., wq–1, wq+1, ..., w n) есть оптимальная смешанная стратегия второго игрока в Г1, то у = (w1, w2, ..., wq–1, 0, wq+1, ..., w n) есть оптимальная смешанная стратегия второго игрока в Г.
Таким образом, из теоремы 2 следует, что, если q-я чистая стратегия второго игрока доминирует какую-либо его чистую стратегию, то q-й столбец в А можно вычеркнуть, положив yq = 0, где yq – q-я компонента оптимальной смешанной стратегии второго игрока. В результате, получаем матрицу А1 меньшей размерности чем А. Если в А1 есть доминирование стратегий, то можно поступать с ней аналогично и уменьшить ее размерность.
Пример 1.
| А = | 4 | 3 | 5 | 1 |
| 4 | 5 | 3 | 5 | |
| 5 | 3 | 5 | 3 | |
| 1 | 5 | 4 | 8 |
Обозначим оптимальные смешанные стратегии первого и второго игроков соответственно через х и у. Очевидно, третья стратегия первого игрока доминирует его первую стратегию, поэтому можно в матрице А вычеркнуть первую строку, положив х1 = 0. Тогда получим новую матрицу
| А1 = | 4 | 5 | 3 | 5 |
| 5 | 3 | 5 | 3 | |
| 1 | 5 | 4 | 8 |
в которой 4-я стратегия второго игрока доминирует его 2-ю стратегию, и поэтому вычеркиваем четвертый столбец, полагая y4 = 0, и получаем новую матрицу
| А2 = | 4 | 5 | 3 |
| 5 | 3 | 5 | |
| 1 | 5 | 4 |
В этой матрице уже нет доминирования. Таким образом, исходную игру с матрицей порядка 4´4 с помощью доминирования свели к игре с матрицей порядка 3´3.
Пример 2.
Рассмотрим игру со следующей матрицей:
5 2 1
2 1 3
3 6 4
Третья строка этой матрицы доминирует вторую. Исключение второй строки приводит к матрице
5 2 1
3 6 4
Третий столбец в этой урезанной матрице доминирует второй, и исключение второго столбца дает
5 1
3 4
В итоге, если можно найти решение для полученной игры, то его легко использовать для решения исходной игры, просто приписав исключенным строкам и столбцам нулевые вероятности.
Матричные игры обладают еще одним интересным свойством, которое формулируется в виде следующей теоремы.
Теорема 3.
Пусть дана матричная игра Г с матрицей А = (aij) и с ценой игры v. Тогда оптимальные смешанные стратегии игроков матричной игры ГВ с матрицей В = (bij) = (daij + с), где d > 0 совпадают с оптимальными смешанными стратегиями соответствующих игроков в матричной игре Г, а цена игры ГВ равна vB = dv + с.
Пользуясь теоремой 3, можно несколько упрощать элементы матрицы А с тем, чтобы легче было с ними оперировать при нахождении решения игры.
Пример.
Рассмотрим матричную игру с матрицей
| А = | 200 | 300 |
| 600 | 100 |
Если каждый элемент этой матрицы разделить на 100 и затем из полученных элементов вычесть 1, то получим игру с матрицей
| В = | 1 | 2 |
| 5 | 0 |
которая имеет более простые элементы. Здесь проведено следующее преобразование:
bij = 0,01×aij – 1, т.е. d = 0,01, c = –1.
В этой игре нет седловой точки в чистых стратегиях. Поэтому для решения игры с матрицей В обозначим через х = (x1, x2), у = (y1, у2) оптимальные смешанные стратегии соответственно первого и второго игроков, v – цена игры с матрицей A, vB – цена игры с матрицей В.
Согласно следствию из теоремы 1, х и у должны удовлетворять соотношениям:
x1 + 5x2 ³ vB y1 + 2y2 £ vB
2x1 ³ vB 5y1 £ vB
x1 + x2 = 1 y1 + y2 = 1
Предположим, что все эти неравенства являются равенствами. Позже будет показано, что это всегда так, если в матричной игре с матрицей порядка 2´2 нет седловой точки в чистых стратегиях. Тогда получим
x1 + 5x2 = vB y1 + 2y2 = vB
2x1 = vB 5y1 = vB
x1 + x2 = 1 y1 + y2 = 1
Решив данную систему, получим:
vB = 3/5, x1 = 3/10, x2 = 7/10, y1 = 3/25, y2 = 22/25
Тогда решением матричной игры с матрицей А будет
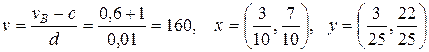
Замечание.
Отметим, что исключение доминируемых (не строго!) стратегий может привести к потере некоторых решений. Если же исключаются только строго доминируемые стратегии, то множество решений игры не изменится.
Пример 3.
Пусть G = (Х,Y,А), где Х = {1, 2, 3, 4}; Y = {1, 2, 3, 4}, а функция выигрыша А задана следующим образом:
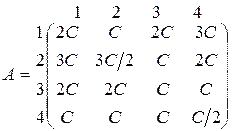
где С > 0.
Решение.
Прежде всего заметим, что по теореме 3 достаточно решить игру G1 = (Х, Y, А), где А1 = 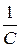 А . В матричной форме игра G1 определяется матрицей выигрышей
А . В матричной форме игра G1 определяется матрицей выигрышей
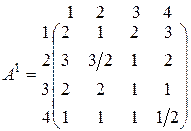
Элементы четвертой строки этой матрицы “ £ ” соответствующих элементов третьей строки и поэтому третья стратегия игрока 1 доминирует над четвертой. Кроме того, элементы первого столбца матрицы А1 “ ³ ” соответствующих элементов второго столбца, Следовательно, вторая стратегия игрока 2 доминирует над его первой стратегией.
Далее, из теоремы 1 и 2 следует, что всякое решение игры
G2 = (Х \{4}, Y \{1}, А1)
является решением игры G1. В матричной форме игру G2 можно представить матрицей
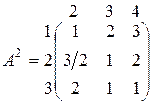 .
.
Очевидно, что элементы второй строки “ ³” полусуммы соответствующих элементов первой и третьей строк. Кроме того, элементы третьего столбца матрицы А2 “ ³“ соответствующих элементов второго столбца. Применяя теорему3, получим, что всякое решение игры
G 3 = (Х \ {4,2}, Y \ {1,4}, А2)
является решением игры G 2, а следовательно и игры G 1. Игра G 3 определяется матрицей
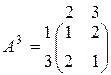 .
.
Матрица А 3 не имеет седловой точки, т.к. не выполнено равенство
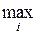
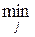
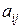 =
= 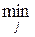
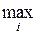
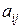 ,
,
а игра G3 не имеет решения в чистых стратегиях, т.е. оптимальные стратегии игроков являются смешанными. Эти стратегии (в данном случае) легко найти из анализа структуры матрицы А3. Поскольку матрица А3 симметрична, можно предположить, что игроки в оптимальной стратегии используют свои чистые стратегии с равными вероятностями.
Действительно, если игрок 1 выбирает с равными вероятностями стратегии 1 и 3, то при применении любой из двух чистых стратегий игроком 2 математическое ожидание выигрыша игрока 1 будет равным либо
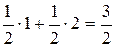 , либо
, либо 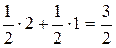 .
.
Аналогично, если игрок 2 использует свои чистые стратегии 2 и 3 с равными вероятностями, то математическое ожидание его проигрыша будет равно 3/2. Следовательно, указанные стратегии являются оптимальными в игре G3, а величины 3/2 – значением игры G3. Из предыдущего следует, что эти стратегии оптимальны и в G1.
Таким образом, стратегия Х = (1/2, 0, 1/2, 0) является оптимальной стратегией игрока 1, стратегия Y = (0, 1/2, 1/2, 0) – оптимальной стратегией игрока 2 в игре G1, а значение игры G1 равно 3/2. В силу свойства 4 решением игры G будет тройка (Х, Y, 3С/2).








