Е(х, 1/4) £ Е(1/2,1/4) £ Е(1/2, у)
Это неравенство можно принять за определение оптимальных частот для любой игры 2´2.
Итак, если Е(х, у) – математическое ожидание выигрыша первого игрока, когда он выбирает 1 с частотой х, а 2 с частотой (1 – х), а второй игрок выбирает 1 с частотой у, а 2 с частотой (1 – у), то мы говорим, что х0 есть оптимальная частота первого игрока, а у0 – оптимальная частота для второго игрока, если для всех 0 £ х £ 1 и 0 £ у £ 1
Е(х, у0) £ Е(х0, у0) £ Е(х0, у)
Свойства оптимальных смешанных стратегий.
Основная теорема теории игр
Лемма
Для любой матричной игры с матрицей А справедлива одна из двух альтернатив:
1) существует такая смешанная стратегия х = (х1, …, х m), что
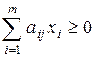 (j = 1, 2, …, n);
(j = 1, 2, …, n);
2) существует такая смешанная стратегия y = (y1, …, yn), что
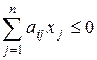 (i = 1, 2, …, m).
(i = 1, 2, …, m).
Основная теорема теории игр (теорема о минимаксе)
Для матричной игры с любой матрицей А величины
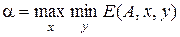 и
и 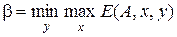
существуют и равны между собой.
Или другими словами:
Всякая прямоугольная игра имеет цену; игрок в прямоугольной игре всегда имеет оптимальную стратегию.
Т.е. любая конечная антагонистическая игра имеет, по крайней мере, одно решение, быть может, в смешанных стратегиях, т.е. существуют такие
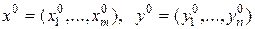 ,
,
что
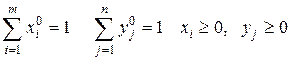
При этом
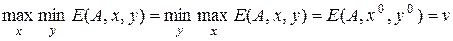
Теорема 1
Для того чтобы в матричной игре с ценой игры v смешанная стратегия х0 первого игрока была оптимальной, необходимо и достаточно для любой смешанной стратегии у второго игрока выполнение неравенства
v £ Е (А, хо, у).
Аналогично для второго игрока, чтобы смешанная стратегия у0 была оптимальной, необходимо и достаточно для любой смешанной стратегии х первого игрока выполнение неравенства
Е (А, х, уо) £ v.
Следствие.
Для того чтобы х0 = (х10, х20, ..., х m) была оптимальной смешанной стратегией матричной игры с матрицей А и ценой игры v, необходимо и достаточно выполнение следующих неравенств
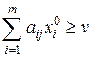 (j = 1, 2, …, n) (1)
(j = 1, 2, …, n) (1)
Аналогично для второго игрока: чтобы у0 = (у10, y20, ..., yn0) была оптимальной смешанной стратегией второго игрока, необходимо и достаточно выполнение следующих неравенств:
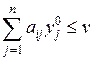 (i = 1, 2, …, m) (2)
(i = 1, 2, …, m) (2)
Из этого следствия вытекает: чтобы установить, являются ли предполагаемые (х, у) и v решением матричной игры, достаточно проверить, удовлетворяют ли они неравенствам (1) и (2). С другой стороны, найдя неотрицательные решения неравенств (1) и (2) совместно со следующими уравнениями
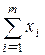 = 1,
= 1, 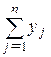 = 1, (3)
= 1, (3)
получим решение матричной игры.
Итак, решение матричной игры сводится к нахождению неотрицательных решений линейных неравенств (1), (2) и линейных уравнений (3).
Теорема 2
Пусть имеется матричная игра с матрицей А, ценой игры v, оптимальными смешанными стратегиями х = (х1, ..., х m), у = (у1, ..., у n) соответственно первого и второго игроков.
Тогда, если для некоторого i будет
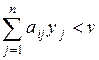 ,
,
то х i = 0;
если для некоторого j будет
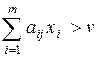 ,
,
то у j = 0.
Пример
Найти решение матричной игры со следующей матрицей:
| А= | 1 | –1 | –1 |
| –1 | –1 | 3 | |
| –1 | 2 | –1 |
На основании следствия из теоремы 1 для нахождения решения этой игры следует найти неотрицательные х1, х2, х3, у1, у2, у3, удовлетворяющие следующим соотношениям:
х1 – х2 – х3 ³ v y1 – y2 – y3 £ v
–х1 – х2 + 2х3 ³ v (a) – y1 – y2 + 3y3 £ v (b)
–х1 + 3х2 – х3 ³ v –y1 + 2y2 – y3 £ v
х1 + х2 + х3 = 1 y1 + y2 + y3 = 1
Причем системы можно решать вместе или отдельно.
Рассмотрим сначала систему (a). Для ее решения можно сначала заменить все неравенства на равенства и попробовать их решить. Если получатся все неотрицательные значения х1, х2, х3, то получено решение игры. Решая систему уравнений
х1 – х2 – х3 ³ v
–х1 – х2 + 2х3 ³ v
–х1 + 3х2 – х3 ³ v
х1 + х2 + х3 = 1
каким-либо известным способом, получим
х1 = 6/13, х2 = 3/13, х3 = 4/13, v = –1/13.
Поскольку значения х1, х2, х3 неотрицательные, они определяют оптимальную смешанную стратегию первого игрока. Если бы в результате решения этой системы получили хоть одно отрицательное значение x i,, то это значит: предположение о том, что все неравенства (a) можно заменить уравнениями, несправедливо и надо только часть неравенств заменить равенствами и решать уже такую систему. Перебирая последовательно все возможные комбинации равенств и неравенств и решая их, получим искомое решение. Это решение обязательно будет найдено, так как оно существует согласно основной теореме теории игр (теореме о минимаксе).
Составляя теперь систему уравнений для второго игрока и решая ее, получим
y1 = 6/13, y2 = 4/13, y3 = 3/13.
Поскольку полученные значения у неотрицательные, они составляют оптимальную смешанную стратегию второго игрока. Итак, решением игры является
x = (6/13, 3/13, 4/13),
y = (6/13, 4/13, 3/13),
v = –1/13.
Способы решения матричных игр








