Оптимальные смешанные стратегии
Исследование в матричных играх начинается с нахождения ее седловой точки в чистых стратегиях. Если матричная игра имеет седловую точку в чистых стратегиях, то нахождением этой седловой точки заканчивается исследование игры. Если же в игре нет седловой точки в чистых стратегиях, то можно найти нижнюю и верхнюю чистые цены этой игры, которые указывают, что первый игрок не должен надеяться на выигрыш больший, чем верхняя цена игры, и может быть уверен в получении выигрыша не меньше нижней цены игры.
В случае отсутствия ситуации равновесия
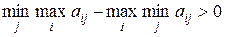
и максиминная и минимаксная стратегии не являются оптимальными. Более того, игрокам бывает невыгодно их придерживаться, так как они могут получить больший выигрыш. Однако сообщение о выборе стратегии противнику может привести к еще большим потерям, чем в случае максиминной или минимаксной стратегии.
Пример
Найти решение игры
| min | |||
| А= | 7 | 3 | 3 |
| 2 | 5 | 2 | |
| max | 7 | 5 |
Для такой матрицы a = 3, а b = 5, т.е. данная матрица не имеет седловой точки (нет ситуации равновесия). Обозначим через i0 максиминную стратегию первого игрока (i0 = 1), а минимаксную стратегию второго игрока через j0 (j0 = 2). Пусть второй игрок придерживается стратегии j0 = 2, а первый игрок выберет стратегию i = 2. Тогда последний получит выигрыш 5, т.е. на 2 единицы больше, чем максимин. Однако если второй игрок догадается о выборе первого игрока, то он изменит стратегию на j = 1, и тогда первый получит выигрыш лишь 2 единицы, т.е. на единицу меньше, чем в случае максимина. Аналогичные рассуждения можно провести и для второго игрока.
При многократном повторении матричных игр без седловой точки в виде партий игроки каждый раз применяют свои стратегии таким образом, что их противники не догадываются об их содержании, и на этом пути в среднем достигают определенных выигрышей, сыграв всю серию партий. Эти выигрыши в среднем больше нижней цены игры и меньше верхней цены игры. Чем больше это среднее значение, тем лучше стратегии применяет игрок.
Поэтому игрокам целесообразно выбирать свои стратегии случайно, с определённой вероятностью, т.е. определять распределение вероятностей на множестве чистых стратегий, а затем предоставить выбор конкретной чистой стратегии случайному механизму.
Выбор игроками своих чистых стратегий с некоторыми наперед заданными вероятностями тоже является некоторой стратегией. В отличие от чистых стратегий, такие стратегии называются смешанными.
Определение.








