Таким образом, исходя из (4), седловой элемент является минимальным в i0-й строке и максимальным в j0-м столбце в матрице А.
Отыскание седловой точки матрицы А происходит следующим образом: в матрице А последовательно в каждой строке находят минимальный элемент и проверяют, является ли этот элемент максимальным в своем столбце. Если он является таковым, то он и есть седловой элемент, а пара стратегий, соответствующая ему, образует седловую точку.
Пара чистых стратегий (i0, j0) первого и второго игроков, образующая седловую точку и седловой элемент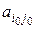 
, называется решением игры.
Чистые стратегии i0 и j0, образующие седловую точку, называются оптимальными чистыми стратегиями соответственно первого и второго игроков.
Итак, если платежная матрица такова, что (3) имеет место, то поиск оптимального способа игры заканчивается. Но далеко не для всех матриц данное условие выполняется, т.е. не у всех матриц существует седловая точка.
Пример 1.
| min | |||
| А= | 1 | –1 | –1 |
| –1 | 1 | –1 | |
| max | 1 | 1 |
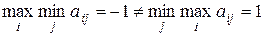. Седловой точки нет.
Пример 2.
Найти решение игры
| min | ||||
| А= | 21 | 11 | 31 | 11 |
| 32 | 0 | 4 | 0 | |
| max | 32 | 11 | 31 |
(1, 2) – седловая точка (значение 11).
Оптимальная чистая стратегия первого игрока – первая (i0 = 1), оптимальная чистая стратегия второго игрока – вторая (j0 = 2), цена игры равна 11 (v = 11).
Пример 3.
Найти решение игры
| min | ||||
| А= | 12 | 13 | 12 | 12 |
| 10 | 31 | 9 | 9 | |
| max | 12 | 31 | 12 |
Две седловые точки (1, 1) и (1, 3) (значение 12).
В этой игре два оптимального решения: i0 = 1, j0 = 1, v = 12;
i0 = 1, j0 = 3, v = 12.
Пример 4
Найти решение игры
| min | ||||
| А= | 1 | –3 | –2 | –3 |
| 0 | 5 | 4 | 0 | |
| 2 | 3 | 2 | 2 | |
| max | 2 | 5 | 4 |
Седловой точкой является пара (i0 = 3; j0 = 1), при которой v = a = b = 2.
Заметим, что хотя выигрыш в ситуации (3;3) также равен 2 = a = b, она не является седловой точкой, т.к. этот выигрыш не является максимальным среди выигрышей третьего столбца.
Пример 5
Найти решение игры
| min | |||
| А= | 10 | 30 | 10 |
| 40 | 20 | 20 | |
| max | 40 | 30 |
Из анализа матрицы выигрышей видно, что a < b, т.е. данная матрица не имеет седловой точки.
Пример 6 . Сражение в море Бисмарка.
В 1943 году японский адмирал Кимура получил приказ переправить военный контингент через море Бисмарка к Новой Гвинее. Американский генерал Кинни получил приказ на перехват и бомбардировку японского флота. Кимура имел выбор между двухдневным маршрутом (северным) и трехдневным (южным). В свою очередь Кинни должен был решить, по какому маршруту послать самолеты в поисках японского транспорта: северному или южному. В случае ошибки самолеты возвращались в конце дня на свои базы и на следующий день могли быть посланы по другому маршруту.
Описанная ситуация может быть представлена следующей матрицей:
| Кимура | |||
| север | юг | ||
| Кинни | север | 2, –2 | 2, –2 |
| юг | 1, –1 | 3, –3 | |
Выигрыши: (Кинни, Кимура).
Поскольку мы имеем игру с нулевой суммой, то ее можно свести к антагонистической игре с матрицей:
| min | |||
| А= | 2 | 2 | 2 |
| 1 | 3 | 1 | |
| max | 2 | 3 |
Будем искать решение в чистых стратегиях:
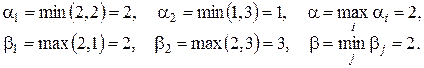
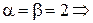игра имеет седловую точку: (Север, Север).
Пример 7
Найти решение игры
| min | |||||
| А= | 5 | 3 | 4 | 3 | 3 |
| 7 | 2 | 0 | –2 | –2 | |
| 10 | –1 | –4 | 2 | –4 | |
| max | 10 | 3 | 4 | 3 |
Игра имеет два решения: i0 = 1, j0 = 2, v = 3
i0 = 1, j0 = 4, v = 3