Рассмотрим прямоугольную игру m´n с матрицей выигрышей А.
| А = | а11 | … | a1j | … | а1n |
| … | … | … | … | … | |
| ai1 | … | aij | … | ain | |
| … | … | … | … | … | |
| am1 | … | amj | … | amn |
Исследуем матрицу выигрышей с точки зрения первого игрока. Если он выберет стратегию 1, то ему будет заплачено как минимум min а1j. Если он выберет i-ю стратегию, ему будет заплачено, по меньшей мере, min aij (i = 1, …, m). Таким образом, он должен выбрать такую стратегию, чтобы min aij был как можно больше, т.е. выбор i-ой стратегии осуществляется как
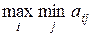 .
.
Аналогично, платежи второму игроку – это элементы матрицы А со знаком минус, т.е. для второго игрока существует выбор, который гарантирует ему, что он получит по меньшей мере
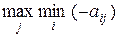
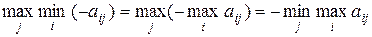 .
.
Таким образом, первый игрок может гарантировать себе выигрыш 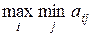 , а второй может играть так, что первый не выиграет у него больше, чем
, а второй может играть так, что первый не выиграет у него больше, чем 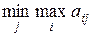 .
.
Для нахождения гарантированного выигрыша первого игрока для каждого значения i (i = 1, 2, ..., m) определяется минимальное значение выигрыша в зависимости от применяемых стратегий второго игрока
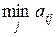 (i = 1, 2, ..., m),
(i = 1, 2, ..., m),
т.е. определяется минимальный выигрыш для первого игрока при условии, что он применит свою i-ю чистую стратегию, затем из этих минимальных выигрышей отыскивается такая стратегия i = i0, при которой этот минимальный выигрыш будет максимальным, т.е. находится
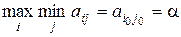 . (1)
. (1)
Такая стратегия называется максиминной.
Определение.
Число a, определенное по формуле (1), называется нижней чистой ценой игры и показывает, какой минимальный выигрыш может гарантировать себе первый игрок, применяя свои чистые стратегии при всевозможных действиях второго игрока.
Второй игрок при оптимальном своем поведении должен стремиться по возможности за счет своих стратегий максимально уменьшить выигрыш первого игрока. Поэтому для второго игрока отыскивается
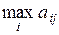
т.е. определяется максимальный выигрыш первого игрока, при условии, что второй игрок применит свою j-ю чистую стратегию, затем второй игрок отыскивает такую свою j = j1 стратегию, при которой первый игрок получит минимальный выигрыш, т.е. находит
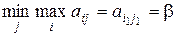 (2)
(2)
Такая стратегия называется минимаксной.
Определение.
Число b, определенное по формуле (2), называется чистой верхней ценой игры и показывает, какой максимальный выигрыш за счет своих стратегий может гарантировать себе первый игрок. Другими словами, применяя свои чистые стратегии, первый игрок может обеспечить себе выигрыш не меньше a, а второй игрок за счет применения своих чистых стратегий может не допустить выигрыш первого игрока больше, чем b.
Нижняя (a) и верхняя (b) цены игры всегда связаны соотношением 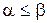 .
.
Определение.
Если в игре с матрицей А нижняя и верхняя чистые цены игры совпадают, т.е.
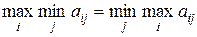 (a = b),
(a = b),
то говорят, что эта игра имеет седловую точку в чистых стратегиях и чистую цену игры:
v = a = b. (3)
Ситуация (i0, j0) называется равновесной, цена игры совпадает с элементом 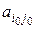 платежной матрицы v =
платежной матрицы v = 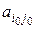 , элемент
, элемент 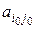 называется седловым элементом матрицы или точкой равновесия.
называется седловым элементом матрицы или точкой равновесия.
Определение.
Седловая точка – это пара чистых стратегий (i0, j0) соответственно первого и второго игроков, при которых достигается равенство a = b.
В понятие седловой точки вложен следующий смысл: если один из игроков придерживается стратегии, соответствующей седловой точке, то другой игрок не сможет поступить лучше, чем придерживаться стратегии, соответствующей седловой точке. Имея в виду, что лучшее поведение игрока не должно приводить к уменьшению его выигрыша, а худшее – может приводить к уменьшению его выигрыша, эти условия можно записать математически в виде следующих соотношений:
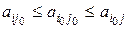 (4)
(4)
где i, j – любые чистые стратегии соответственно первого и второго игроков; (i0, j0) – стратегии, образующие седловую точку.








