Игра называется игрой с нулевой суммой, если сумма выигрышей всех игроков равна нулю (т.е. каждый игрок выигрывает только за счет проигрыша других).
Рассмотрим партию с игроками Р1, Р2, …, Р n и р i (i = 1, …, n) – платежи i-му игроку в конце партии (если Р i платит сам, то pi – отрицательно).
Если правила таковы, что 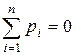 , то партия называется партией с нулевой суммой. Если любая возможная партия некоторой игры имеет нулевую сумму, то игра называется игрой с нулевой суммой
, то партия называется партией с нулевой суммой. Если любая возможная партия некоторой игры имеет нулевую сумму, то игра называется игрой с нулевой суммой
Игра двух лиц с нулевой суммой называется антагонистической, так как цели игроков в ней прямо противоположные: выигрыш одного игрока происходит только за счет проигрыша другого.
Антагонистические игры, в которых оба игрока имеют конечные множества стратегий, называются матричными.
Примером игры с ненулевой суммой могут быть торговые взаимоотношения между странами. В результате применения своих стратегий все страны могут быть в выигрыше. Всякая игра, в которой надо вносить взнос некоторому лицу за право принимать участие в ней, является игрой с ненулевой суммой. Действительно, в этом случае всегда в выигрыше получается некоторое лицо, которое не принимает участия в игре, а получает взнос от игроков, теряющих свой капитал за счет этих взносов. Другим примером служит лотерея: в ней организатор всегда имеет выигрыш, а участники игры –лица, купившие лотерейные билеты, – в сумме получают выигрыш меньше, чем они внесли.
По виду функций выигрыша игры делятся на: матричные, биматричные, непрерывные, выпуклые, сепарабельные, типа дуэлей и др.
Матричная игра – это конечная игра двух игроков с нулевой суммой, в которой задаются выигрыши первого игрока в виде матрицы (строка матрицы соответствует номеру применяемой стратегии первого игрока, столбец – номеру применяемой стратегии второго игрока; на пересечении строки и столбца матрицы находится выигрыш первого игрока, соответствующий применяемым стратегиям). Выигрыш второго игрока равен проигрышу первого
Для матричных игр доказано, что любая из них имеет решение, и оно может быть легко найдено путем сведения игры к задаче линейного программирования.
Биматричная игра – это конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии первого игрока, столбец – стратегии второго игрока, на пересечении строки и столбца в первой матрице находится выигрыш первого игрока, во второй матрице – выигрыш второго игрока).
Для биматричных игр также разработана теория оптимального поведения игроков, однако решать такие игры сложнее, чем обычные матричные.
Непрерывной считается игра, в которой функция выигрышей каждого игрока является непрерывной в зависимости от стратегий. Доказано, что игры этого класса имеют решения, однако не разработано практически приемлемых методов их нахождения. Простым примером непрерывной игры двух игроков является следующая: первый игрок выбирает число х из отрезка [0, 1], и второй игрок выбирает число у из отрезка [0, 1], после чего первый игрок выигрывает х – у2, а второй проигрывает столько же. Очевидно функция х – у2 является непрерывной и поэтому игра также считается непрерывной. Согласно теореме существования решения такая игра имеет решение.
Если функция выигрышей является выпуклой, то такая игра называется выпуклой. Для них разработаны приемлемые методы решения, состоящие в отыскании чистой оптимальной стратегии (определенного числа) для одного игрока и вероятностей применения чистых оптимальных стратегий другого игрока. Такая задача решается сравнительно легко.
Если функция выигрышей может быть представлена в виде суммы произведений функций от одного аргумента, то такая игра называется сепарабельной (разделимой). С помощью определенных преобразований ее решение сводится к решению игры с билинейной функцией выигрышей и к определению неподвижной точки при специальном отображении множеств элементов, соответствующих стратегиям.
Игры типа дуэлей характеризуются моментом выбора хода и вероятностями получения выигрышей в зависимости от времени, прошедшего от начала игры до момента выбора. Например, существуют интерпретации таких игр в экономических ситуациях: каждая фирма делает вклад своего капитала в определенный момент времени с целью овладения рынком сбыта. Чем раньше она сделает свой вклад, тем меньшая вероятность овладеть рынком, но, делая свой вклад слишком поздно, она теряет рынок сбыта. Функция выигрышей игроков в играх типа дуэлей принимает специальный вид: она непрерывна при разных значениях моментов времени, когда игроки делают ходы, и она разрывна при совпадении моментов хода игроков. Так что нет гарантий существования решений для игр типа дуэлей. Существуют определенные методы решения таких игр.
По количеству ходов игры делятся на одношаговые и многошаговые. Одношаговые (статические) игры заканчиваются после одного хода каждого игрока. Например, матричная игра является одношаговой, так как при этом каждый игрок делает только один ход и потом происходит распределение выигрышей.
Многошаговые (динамические) игры делятся на позиционные, стохастические, дифференциальные, типа дуэлей и др.
В позиционных играх может быть несколько игроков, каждый из которых может последовательно во времени делать несколько ходов. Выигрыши определяются в зависимости от исходов игры (применяемых стратегий). Такие игры с помощью определенных способов сводятся к матричным играм и могут решаться присущими им методами.
Если в игре производятся ходы, приводящие к выбору определенных позиций, причем имеется определенная вероятность возврата на предшествующую позицию, то такая игра является стохастической.
Если в многошаговой игре допускается делать ходы непрерывно и подчинять поведение игроков некоторым условиям, описываемым дифференциальными уравнениями, то такие игры являются дифференциальными. Например, в играх типа погони каждый объект может двигаться, подчиняясь определенным условиям, описываемым обыкновенными дифференциальными уравнениями. Цель одного объекта – достичь определенной области, цель другого – не допустить первого до этой области. Выигрыш оценивается определенным числом (функцией).
В зависимости от состояния информации различают игры с полной информацией и с неполной информацией. Если на каждом ходе игры каждому игроку известно, какие выборы были сделаны игроками раньше, то это игра с полной информацией.
Примерами таких игр являются шашки, шахматы. Если в игре не все известно о предыдущих выборах, то это игра с неполной информацией.
Доказано, что всякая игра с полной информацией имеет решение в виде седловой точки в чистых стратегиях. Например, для игры в шахматы это значит, что для каждого игрока имеется такая стратегия, придерживаясь которой, игрок либо выигрывает, либо сведет партию в ничью. Сложность заключается в отыскании такой стратегии. Существуют и другие виды игр, которые здесь не рассматриваются. Возможны и некоторые другие принципы классификации игр.
Игра одного игрока с нулевой суммой не представляет никаких проблем, поскольку, что бы игрок ни делал, он получает ноль. Поэтому он может выбирать любой ход.
При игре одного лица с ненулевой суммой игроку нужно решить обычную задачу на max: он должен выбрать из различных, имеющихся у него альтернатив ту, которая дает ему max выигрыш.
Матричные антагонистические игры
Будем рассматривать игры двух лиц с нулевой суммой, в которой каждый игрок имеет лишь один ход. Каждый игрок делает по одному ходу, затем один игрок платит другому сумму, которая зависит от выборов, сделанных двумя игроками.
Матричная игра двух игроков с нулевой суммой может рассматриваться как следующая абстрактная игра двух игроков.
Первый игрок имеет m стратегий i = 1, 2, ..., m, второй имеет n стратегий j = 1, 2, ..., n. Каждой паре стратегий (i, j) поставлено в соответствие число aij, выражающее выигрыш первого игрока за счет второго игрока, если первый игрок применит свою i-ю стратегию, а второй – свою j-ю стратегию.
Каждый из игроков делает один ход: первый игрок выбирает свою i-ю стратегию (i =1, 2, …, m), второй – свою j-ю стратегию (j = 1, 2, ..., n), после чего первый игрок получает выигрыш aij за счет второго игрока (если aij, < 0, то это значит, что первый игрок платит второму сумму | aij |). На этом игра заканчивается.
Каждая стратегия игрока i = 1, 2, …, m; j = 1, 2, ..., n часто называется чистой стратегией.
Матричная игра двух игроков с нулевой суммой далее будет называться просто матричной игрой. Очевидно, матричная игра относится к антагонистическим играм. Из ее определения следует, что для задания матричной игры достаточно задать матрицу А = (aij) порядка m ´ n выигрышей первого игрока.
Данная игра записывается в виде матрицы выигрыша первого игрока. Строка матрицы соответствует номеру применяемой стратегии первого игрока, столбец – номеру применяемой стратегии второго игрока; на пересечении строки и столбца матрицы находится выигрыш первого игрока, соответствующий применяемым стратегиям. Элементы aij – значение функции выигрыша первого игрока в ситуации, когда первый игрок выбрал свою i-ю стратегию, а второй игрок – свою j-ю стратегию. Для второго игрока в этом случае aij – проигрыш.
| А = | а11 | … | a1j | … | а1n |
| … | … | … | … | … | |
| ai1 | … | aij | … | ain | |
| … | … | … | … | … | |
| am1 | … | amj | … | amn |
Такие игры называются прямоугольными.
Для формализации реальной конфликтной ситуации в виде матричной игры надо выделить и перенумеровать чистые стратегии каждого игрока и составить матрицу выигрышей.








