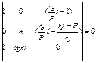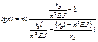27 Устойчивость стержня с упругой заделкой на одном конце и свободным другим концом
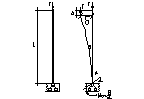 Схема потери уст. Податливость опоры харак парм a- углом поворота от дейст единич момента М=1. Применяя стат метод, состав условие равновесия
Схема потери уст. Податливость опоры харак парм a- углом поворота от дейст единич момента М=1. Применяя стат метод, состав условие равновесия 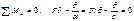
Находим критич нагрузку 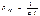 . Решаем задачу энергетическим методом. Выразим изменение упругой энергии сист ч/з работу силыF и опорного момента
. Решаем задачу энергетическим методом. Выразим изменение упругой энергии сист ч/з работу силыF и опорного момента 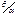 затраченную при переходе системы из первоначального в отклоненное сост. Работа силы F опред
затраченную при переходе системы из первоначального в отклоненное сост. Работа силы F опред 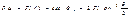 . Учитыв малость перемещ D заменим ф-ю
. Учитыв малость перемещ D заменим ф-ю 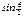 углом. Тогда
углом. Тогда 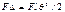
Работа, соверш опорным моментом опред 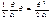
Изменение полной упругой энергии 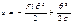
Энергетическим критерием потери устойчивости сист явл 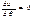
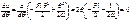 Получаем условие для предел критич силы
Получаем условие для предел критич силы 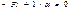 откуда
откуда 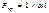
29. Расчет неразрезных балок методом фокусов определение опорных моментов с помощью моментных фокусных отношений.
Установлено что в каждом ненагруженном пролете при положении нагрузки справа (или слева) от него эпюра моментов имеет нулевую точку, причем местоположении этой точки постоянно и не зависит от интенсивности и вида загружения пролета. Эта точка называется моментным фокусом. Различают правые и левые моментные фокусы. Левым(правым) моментным фокусом, наз-ся нулевая точка эпюры моментов данного пролета при нагружении одного или нескольких пролетов, расположенных правее(левее) рассмат-го.
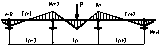
Отношение моментов ненаеруженного пролета яв-ся постоянным. 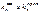 фокусные отношения.
фокусные отношения. 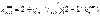
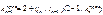
При шарнирном опирании крайнего пролета точка нах-ся в шарнире крайнего пролета 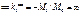 При заделанном конце балки
При заделанном конце балки 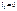 - доп пролет.
- доп пролет. 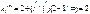
Если нагружен только один пролет n то опорные моменты для этого пролета получены из совместного решения двух Ур-ий 3-х моментов сост-х для опор n-1 и n. 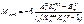
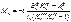
где 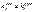 - соот-во левое и правое фокусные отношения пролета n;
- соот-во левое и правое фокусные отношения пролета n; 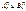 ”фиктивная” реакция соот-во на левом и правом концах нагруженного пролета n; Если крайняя левая опора шар-я, то
”фиктивная” реакция соот-во на левом и правом концах нагруженного пролета n; Если крайняя левая опора шар-я, то 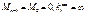 и по этому
и по этому 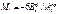 Остальные опорные моменты могут быть получены через фокусные отношения. При нагруженни пролета n они будут равны.
Остальные опорные моменты могут быть получены через фокусные отношения. При нагруженни пролета n они будут равны.
44. Резонансное явление, коэф динамичности при вынуждаемых колеб-х без учета сил сопротивления.
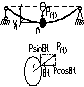
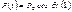
Вынужденные колебания упруг сист при действии силы Р(t), изменяющейся по гармоническому закону (1). Они опред-ся 3-м слагаемым ДУ 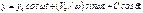 т е
т е 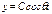 , где С-амплитуда вынужденных колебаний. Найдем С из ДУ:
, где С-амплитуда вынужденных колебаний. Найдем С из ДУ:
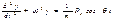 т к
т к 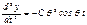 получим
получим 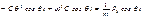 сократим на
сократим на 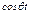 и найдем С
и найдем С 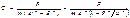 где
где 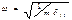 -частота колебаний,
-частота колебаний, 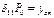 -статический прогиб балки при том, что вместо Р(t) приложена её амплитуда.
-статический прогиб балки при том, что вместо Р(t) приложена её амплитуда. 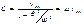 где
где 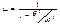 динамический коэффициент.
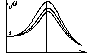
динамический коэффициент. 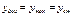 m- максимальное отклонение называется динамическим прогибом балки от положения статич равновесия. График изменения m
m- максимальное отклонение называется динамическим прогибом балки от положения статич равновесия. График изменения m
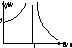
При 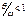 m- возрастает, При
m- возрастает, При 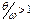 , m=¥ При совпадении частоты вынужденных колебаний q с частотой свободных колебаний w прогибы достигают больших величин. Явление сильно нарастания амплитуд колебаний при совпадении частот q и w называется резонансом (q=w). Резонанс опасен для сооружений поэтому надо принимать меры, чтобы q и w не совпадали. q/w>>1®m-отрицателен, т к происходит сдвиг фаз, внешняя сила на некотором отрезке времени тормозит движение массы m. При
, m=¥ При совпадении частоты вынужденных колебаний q с частотой свободных колебаний w прогибы достигают больших величин. Явление сильно нарастания амплитуд колебаний при совпадении частот q и w называется резонансом (q=w). Резонанс опасен для сооружений поэтому надо принимать меры, чтобы q и w не совпадали. q/w>>1®m-отрицателен, т к происходит сдвиг фаз, внешняя сила на некотором отрезке времени тормозит движение массы m. При 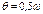 резонанса никогда не будет.
резонанса никогда не будет.
10. Вынужденные колебания системы с конечным числом степеней свободы
Число возмож форм колеб упругой сист = числу степеней свободы. Каждой форме колеб соотв своя частота. Число степ свободы упругой сист опред числом возможных независимых смещений. Для того чтобы установить число степ свободы сисит, несущей сосредоточенной массы необходимо путем постановки связей привести сист к таковой в к-ой невозможны смещения масс. Наименьш число связей необходим для закрепления всех масс будет равно числу степеней свободы.
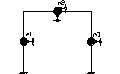
Ст свободы не зависят от того статич определима или неопределима сист. Число степ свободы зависит от статической точности расчета. Поэтому определение числа степеней свободы носит условный характер. Если сист несет не сосредоточ, а распредел массы, то эта сист будет иметь бесконечное число степ свободы. Расчет такой системы значит сложнее остальных.Число возможных форм колебаний упругой сист = числу степ свободы. Каждой форме колеб соот своя частота. Для сист с n-степенями свободы возможны n-различных частот к-ым соот n различных форм колебаний. Совокупность всех частот упруго системы носит название спектра частот. Для пркатических целей в расчете обычно став задача опред одной наименьшей частотой, подобно тому кака при расчете на устойчивость знать одну Ркр Рассм балку к-ая несет n-точечных масс, она имеет n-степеней свободы хар-ся n-частотами свобод колеб. w1, w2, wn .
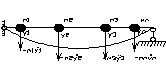
Для определения частот необходимо знать перемещение точек при прилож сосредотогч масс (y1, y2, y3). Эти смещ поисхъод под дейст инерц сил.
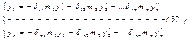
Данная сист ДУ допускает n-частных решений вида
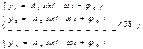
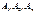 -амплитуды колебаний соотв масс.
-амплитуды колебаний соотв масс.
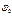 - начальная фаза колебаний
- начальная фаза колебаний
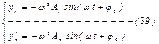
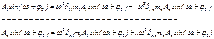
Сократим на 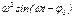 , лев часть в правую, выносим А
, лев часть в правую, выносим А
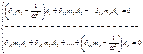
1) А1=А2=А3..=Аn если сист наход в покое
2) Систт вместе с массами соверш колеб А1¹А2¹А3..¹Аn
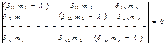
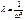
Если определитель 41 раскрыть то мы получим Ур-е 1-ой степени относительно l ркшив к-ое можно найти n-различных корней l1, l2, ln. И соот можно найти частоты свобод колеб w1, w2, wn, В некоторой сист особенно в рамных 2 или 3 частоты могут оказаться численно равными м/у собой. Ур-ие 41 впервые было получено астрономами. Характеристические числа в этом Ур-ии представ собой квадраты периодов планет. В том случае, когда получ вековое Ур-ие 2 или 3 порядка решение Ур-ий не вызывает зхатрудгнеий. Если направление перемещ y1, y2, yn, выбраны так что побочные перемещения 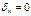 , то сист ДУ 37 и соот ей Ур-ие частот расклад на отдельн Ур-ия содерж только главн перемещ, в этом случае перемещ y1, y2, yn наз главными координ соот ф-мы колебаний.
, то сист ДУ 37 и соот ей Ур-ие частот расклад на отдельн Ур-ия содерж только главн перемещ, в этом случае перемещ y1, y2, yn наз главными координ соот ф-мы колебаний.
Главные формы колеб обособл от др и каждая тз них происходит со своей опред частотой 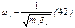 Однако выбрать главн коор для сист с числом ст свободы более 2-х, 3-х явл сложн задачей. Для сист 2 ст свободы это всегда можно сделать, для симметр сист с симметр располож массами и кососимметр ф-ми колеб, при которых силы инерции будут прямосимметр и кососимметр.
Однако выбрать главн коор для сист с числом ст свободы более 2-х, 3-х явл сложн задачей. Для сист 2 ст свободы это всегда можно сделать, для симметр сист с симметр располож массами и кососимметр ф-ми колеб, при которых силы инерции будут прямосимметр и кососимметр.
17. Матричная форма расчета арок
Трехшарнирные арки в матр-ой форме проще рассчитывать с использованием преобразрования базиса нагр-ки. Для трехшарнирной арки с пароболическим очертанием оси 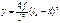
нагруж сосред силами, построить эпюру изгиб-их моментов.
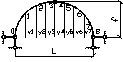
Пролетарки разбиваем на 8 равных частей.
Вектор изгибающих моментов во всех внутренних пронумерованных сечениях арки вер-ой задан-ий нагр-ки можно записать: 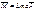
Где 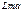 - матрица влияния изгибающих моментов в арке. Вектор изгиб-х моментов в тех-же сечениях арку от самоурав-ного базиса
- матрица влияния изгибающих моментов в арке. Вектор изгиб-х моментов в тех-же сечениях арку от самоурав-ного базиса 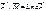
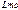 - матрица влияния изгибающих моментов от самоурав-ного базиса
- матрица влияния изгибающих моментов от самоурав-ного базиса 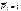
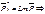
В этом месте пробел в шпоре
Для состав-я матрицы 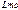 рассчитываем арку на самоуравнев-ю нагр-ку. Эпюры изгиб-х моментов будут локальными с единич-ой ординатой в данном сечении, т.е. эти эпюры будут как и в простой балке. При приложении нагрузки
рассчитываем арку на самоуравнев-ю нагр-ку. Эпюры изгиб-х моментов будут локальными с единич-ой ординатой в данном сечении, т.е. эти эпюры будут как и в простой балке. При приложении нагрузки 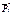 в среднем шарнире изгиб-й момент в этом сечении должен быть равен нулю, а в остальных сечениях отличным от нуля.
в среднем шарнире изгиб-й момент в этом сечении должен быть равен нулю, а в остальных сечениях отличным от нуля. 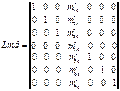
Матрицу изгиб моментов в балке постр-им пользуясь натуральной центробежной матрицей. 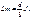
Вектор ихзгибающих моментов в сечениях арки 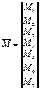
57. Период, круговая частота свободных колебаний с одной степ свободы. Техническая частота.
Периодом колебания Т называется время одного колебания. Период тригонометрических функций равен 2π. Отсюда 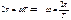
ω-кол-во колебаний за 2π секунд –это и есть круговая частота. Она яв-ся хор-ой сис-мы и выч по ф-ме: 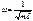
Частота не зависит от начальных возмущений. Частота соб-х колеб-й при учете затухающих выч-ся по ф-ле: 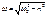
20. Комбинированный способ расчета рам.
Комбинир способ прим как для симметричных так и для не симметричных рам. В этом случае один из методов расчета(напр МС) яв-ся основным, а другой(МП) – вспомогательный, или наоборот. Если в кач-ве основного метода выбран метод расчета сил, то основная сис-ма образуется удалением не всех лишних свазей и считается по этому статич-и неопределимой. Для её расчета на нагрузку и на дейст-ие единич-х неизв-х в кач-ве вспомогательного применяют метод перемещений.
А если основной метод МП, то в основ-й сис-ме уст-ие не все перемещ-я узлов, что ведет к её кинематической неопределенности. Для расчета потребуется в кач-ве вспомогательного МС.
38. Устойчивость арок. Общие сведения.
Расчет на усто-ть относ-ся к 1ому предельному сост-ю. В случае когда арка очерчена по кривой давления, то такая арка работает на центр. сжатие. Если ось арки совпадает с кривой давления, то как и в сжатых прямолинейных стержнях арка может потерять устойчивость переходя в новый вид равновесия при /м дополнительно появляется изгибная форма деф-ций. На цент-е сжет-е раб-т круговые арки при гидростатическом давлении; пораболические арки при дейс-ии равномерно-распределенной верти-й нагр-и по всему пролету. Задачи на устйчивость арок, очерченных по кривой давления и работающих до момента потери уст-ти упругой стали на центр-е сжатие. Рассмотрены задачи уст-ти различных арок: двухшар-х , безшар-х, пораболических. Составлены таблиц, поз-щие решать задачи. Рассмотрим устоцйчивость круговой арки под действием радиальной нагр-и. Такая арка до потери уст-и работает на центральное сжатие (g=gкр), в это время появляется новая форма деформаций-изгиб. При этом потеря устойчивости может произойти по симметричной или кососиметр-й форме.

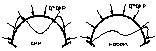
При 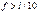 рассм-ем лишь кососим форму потери уст-ти.
рассм-ем лишь кососим форму потери уст-ти.
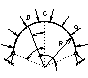
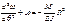
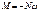
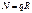

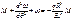
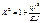
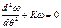
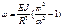
при 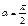
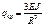
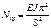
S-длина дуги полуарки.
13. Устойчивость центрально сжатого стержня с упругой заделкой на одном конце и упругоподатливой на другом конце.
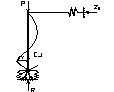
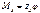
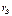 - реакции, кот-е возникают в опоре В от единичнонго смещения по горизонтали.
- реакции, кот-е возникают в опоре В от единичнонго смещения по горизонтали.
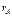 - реактивный момент в другой заделке при повороте на φ=1
- реактивный момент в другой заделке при повороте на φ=1
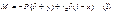
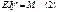
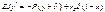
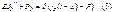
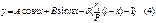 А,В,δ- нужно найти граничные условия:
А,В,δ- нужно найти граничные условия:
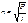
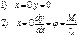
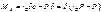
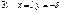
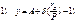
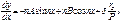
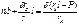
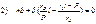
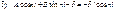
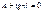
А,В,δ=0 при примолинейном стержне