Рассмотренный выше прием расчета симметричной рамы называется комбинированным способом. Он используется при расчетах симметричных систем на несимметричные нагрузки.
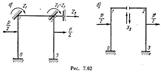
Следовательно, рассчитывая раму методом перемещений при действии обратносиммеричной нагрузки, необходимо составить два уравнения с двумя неизвестными.
Рассчитывая раму на обратносимметричную нагрузку методом сил,, можно воспользоваться основной системой, изображенной на рис. 7.62, б, в которой неизвестным усилием будет лишь поперечная сила X 3; момент же X 2 и продольная сила X 1 при обратносимметричном загружении равны нулю. В этом случае придется решить лишь одно уравнение с одним неизвестным.
Таким образом, при расчете рассматриваемой рамы на обратно-симметричную составляющую заданной нагрузки целесообразно воспользоваться методом сил.
Рассмотренный выше прием расчета симметричной рамы называется комбинированным способом. Он используется при расчетах симметричных систем на несимметричные нагрузки.
14. Статический способ определения коэффициентов и свободных членов системы уравнений в методе перемещений.
Необходимо построить эпюру изгибающих моментов в основной системе от нагрузки и от единичных неизвестных перемещений. Эпюру Мр для левой стойки построим, как для балки с 2-мя заделанными концами, а для ригеля – как для балки с заделкой на одном конце и шарнирной опорой на другом. 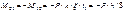
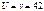
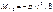
Эпюру 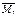 от поворота заделки 1 на угол z=1 построим в ригеле 1-2
от поворота заделки 1 на угол z=1 построим в ригеле 1-2 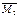 В стержне 1-2 момент отсутствует, т.к. при смещении по направлению z2 этот стержень не деформируется.
В стержне 1-2 момент отсутствует, т.к. при смещении по направлению z2 этот стержень не деформируется.
Все коэффициенты разделим на 2-е группы: а) предст. Реактивный момент во всех единичных заделках. б) коэф. предст. реактивные усилия во введенных стержнях.
Коэффициенты первой группы определяются вырезанием узлов и составлением уравнения равновесия вида 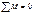 Коэффициенты 2-ой группы определяются с помощью разреза элементов рамы и составлением суммарных уравнений равновесия сил действующих на отсеченную часть
Коэффициенты 2-ой группы определяются с помощью разреза элементов рамы и составлением суммарных уравнений равновесия сил действующих на отсеченную часть 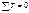
Знаки: реактивное усилие положительно, если направление его действия совпадает с принятым направлением см поворота или линейного смещения узла.
23. Расчет параболических арок.
Аналитический расчет арок: для арки с опорами на одном уровне опорные реакции раскладываются вертикальные и горизонтальные – распор H.
Вертикальные составляющие VA=VB.
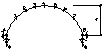
Вертикальные составляющие определяют из уравнений моментов относительно опор:
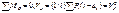
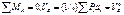
где аi – плече силы Pi относительно опоры А.
Из уравнения 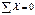 устанавливают, что HA=HB=H.
устанавливают, что HA=HB=H.
Значение распора аналитически определяют из уравнения 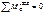
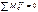
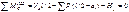
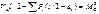
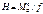
M, Q и N силы в любом сечении арки коэффициентами x, y и углом поворота наклона касательной φ могут быть определены из уравнения моментов относительно точки (x;y) и уравнений проекции проекций сил, действующих на левую или правую часть арки, на касательную и нормаль к оси в точке (x;y).
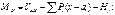
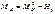
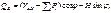
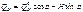
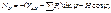
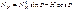
В 3-х шарнирной арке с затяжкой 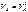 ;
; 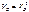 ; усилие в затяжке определяют из уравнения
; усилие в затяжке определяют из уравнения 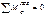 ;
; 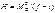
M, Q и N в любом сечении 3-х шарнирной арки с затяжкой будут равны:
а) для участков ниже затяжки 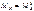 ;
; 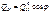 ;
; 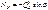
а) для участков выше затяжки 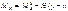 ;
; 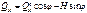 ;
; 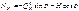
Наличие в арке распора вызывает необходимость создание массивных опор.
Напряжения от совместного действия изгибающего момента и продольной силы проверяют в сечениях, где абсолютное значение момента является наибольшим. 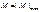 , по формуле
, по формуле 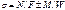
29. Свободные колебания системы с одной степенью свободы. Вывод дифференциального уравнения.
Самая простая задача колебания с одной степенью свободы являются колебания невесомого стержня с приложенной массой.
у – отклонения от статического равновесия сил.
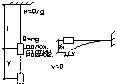
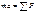 ;
; 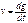 ;
; 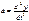 ;
; 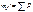
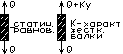
K – сила, сообщающая стержню единичное удлинение.
Ky – реакция, возникающая в стержне при отклонении массы от положения статического равновесия.
Проекция всех сил на ось y: 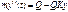 ;
; 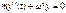 - диф. Однород. Ур. собственного незатух. колебания системы.
- диф. Однород. Ур. собственного незатух. колебания системы.
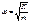 ;
;
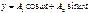 - уравнение гармонических колебаний.
- уравнение гармонических колебаний.
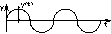
А1 и А2 – постоянные величины, которые необходимо определить из граничных условий.
1)при t=0 – y(t)=yo, A1=yo
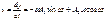
2)t=0; 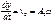 ;
; 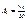 ;
;
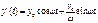 - ур-ие собств. незатух. колебательных движений.
- ур-ие собств. незатух. колебательных движений.
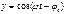 - ур-ие колебательных движений
- ур-ие колебательных движений
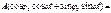
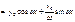
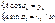
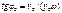 *
*
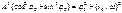
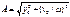
Из ур-ия * определяем: 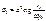
При t=0 из уравнения колебательных движений получаем: 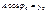 ;
;
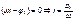 - мах отклонение.
- мах отклонение.
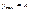 - амплитуда колебательных движений.
- амплитуда колебательных движений.
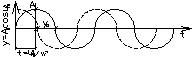
13. Построение эпюр изгибающих моментов и поперечных сил для неразрезных балок. Построение объемлющих эпюр.
Если у балки загружен 1-й пролет, то при помощи фокусных отношений очень просто и быстро определяются все опорные моменты.
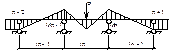
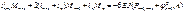
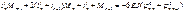 , где
, где 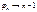
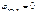
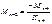
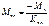
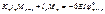
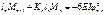
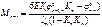
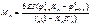 ,
,
где 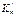 и
и 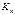 левое и правое фокусные отношения пролета n. Если правая опора шарнирная, то левый опорный момент
левое и правое фокусные отношения пролета n. Если правая опора шарнирная, то левый опорный момент 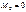
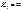 .
.
Правый опорный момент первого загруженного пролёта 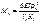
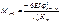 - для крайнего правого нагруженного пролёта
- для крайнего правого нагруженного пролёта
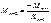
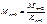
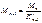
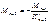
Необходимость нахождения такого сочетания пост-х и врем-х нагрузок, которые вызывают в различных сечениях наибольшие и наименьшие изгибающие моменты и поперечные силы приводящие к необходимости построения обьемляющие эпюр.
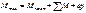
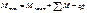
Аналогично находят 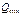 и
и 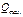
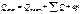
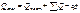
Ординаты 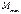 и
и 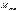 определяют обычно по табличной формуле, построение
определяют обычно по табличной формуле, построение 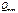 и
и 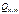 может быть выполнено без таблиц.
может быть выполнено без таблиц.
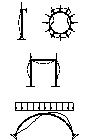
53. Устойчивость круговой двух шарнирной арки под действием радиальной нагрузки.
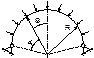
При f<l/10 рассматриваем только кососимметричную форму деформации. 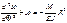
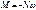
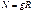
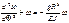
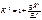
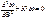
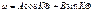
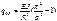 , при
, при 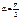
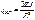
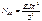 , S – длина дуги полуарки
, S – длина дуги полуарки
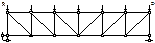
23. Определение частот колебаний балочной фермы с сосредоточенными силами(переход к эквивалентной балке)

Способ перехода к эквивалентной балке состоит в том, что ферма заменяется балкой сплошного сечения обладает жесткостными характеристиками эквивалентной жесткости фермы и тогда частота колебаний фермы определяется, как для балки. Момент инерции искомой балки определяется из условия равенства прогибов фермы и эквивалентной балки в наиболее характерных точках.
Напряжение по середине пролета: 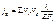
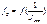 ;
; 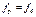 ;
; 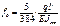 ;
; 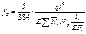 ;
;
Зная момент инерции эквивалентной балки можно определить частоту колебаний фермы по формуле:
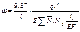
;m=q/g;
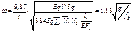 ;
;
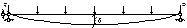
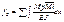 ;
; 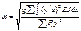 ;
;
Эту формулу можно использовать так же для ферм с непараллельными поясами. Использование приема к эквивалентной балке для определения частоты колебаний в ферме дает удовлетворительные результаты.
16 Расчет рам смешанным способом.
При смешанном методе расчета часть неизвестных представляет собой усилия – силы, моменты (как при расчете методом сил), а другая часть – перемещения – повороты, поступательные смещения (как при расчете перемещений).Степень статической неопределимости 1-ый этаж – 9, 2-ой этаж -2. Число неизвестных угловых и линейных перемещений 1-ый этаж – 2, 2-ой этаж 12. При расчете первого этажа задан. системы проще воспользоваться методом перемещений, а второго - методом сил.
Применение этого метода к рассматриваемой системе позволяет свести задачу к решению четырех уравнений с 4-мя неизвестными вместо 11 – по методу сил и 14 по методу перемещений. За неизвестные удобно принять углы поворота узлов первого этажа и усилия, возникающие в верхнем шарнире. Осн. система получена удаление связей в верхней части рамы и добавлением их в нижней.2-ой этаж 12. При расчете первого этажа задан. 2,л, другую методом перемещений, некоторые удобно рассчитать смешанным методом.истемыи Составим канонические уравнения смешанного метода, смысл к-ых заключается в том, что в основной системе реакции, возникающие во введенных связях по направлению неизвестных перемещений Z1 и Z2, а также перемещения по направлвению неизвестных усилий X3 И Х4 равны нулю:
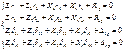
Z1r11 – реакция в осн. системе, возникающая в первой заделке от ее поворота на угол Z1;
Z2r12 – реакция в осн. системе, возникающая в первой заделке от ее поворота на угол Z2;
Х3r13 – реакция в осн. системе, возникающая в первой заделке от сил Х3;
Х4r14 – реакция в осн. системе, возникающая в первой заделке от сил Х4;
R1p – реакция в осн. системе, возникающая в первой заделке от заданной нагрузки.
Сумма перечисленных реакций равна нулю, т.к. в действительности заделки нет, а следовательно нет и ее реакции. Таким образом, первое уравнение является уравнение статики, оно выражает мысль о равенстве нулю реактивного момента, возникающего в первой заделке от действия неизвестных и заданной нагрузки. Такую же мысль выражает и первое уравнение.
Рассмотрим 3-е уравнение и установим смысл каждого его слагаемого:
Z1δ31 – перемещение в основной системе по направлению Х3, возникающее от поворота первой заделки на величину Z1;
Z2δ32 – перемещение в основной системе по направлению Х3, возникающее от поворота первой заделки на величину Z2;
Х3δ33 – перемещение в основной системе по направлению Х3, от сил Х3;
Х4δ34 – перемещение в основной системе по направлению Х3, от сил Х4;
Δ3р – перемещение в осн. системе по направлению Х3, от заданной нагрузки.
Сумма перечисленных перемещений равна нулю, т.к. в действительности верхний шарнир не разрезан, а поэтому точки приложения сил Х3 расходиться не могут. Таким образом третье уравнение выражает мысль о равенстве нулю перемещения; его можно назвать уравнением кинематики.
Коэффициенты при неизвестных системы уравнений смешанного метода связаны между собой соотношениями: 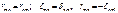 т.е абсолютные значения коэф-ов, располагаюфщихся на побочных диагоналях, удовлетворяют условиям взаминости.
т.е абсолютные значения коэф-ов, располагаюфщихся на побочных диагоналях, удовлетворяют условиям взаминости.
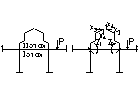
4. Общий способ определения коэф-ов и свободных членов системы канонич. ур-ий метода перемещений.
Основная система метода перемещений получается путем введения дополнительных связей и появлению реактивных моментов во введенных заделках и реактивных сил в дополнительных стержнях. Эти дополн реак силы и моменты можно обратить в 0, если заделку повернуть на углы, равные действит углам поворота узлов рамы и сместить узлы рамы, так чтобы лин перемещ так же были равны действит смещ. После этого деформ основ сист и усилия в ней будут равны деформ и усилиям зад сист. Отрицание реак М и усилий во введен заделках и стержнях основ сист лежит в основе уравн метода перемещ. Уравнения метода перемещ – уравн равновесия.
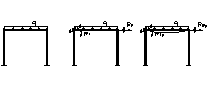
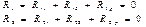
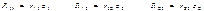
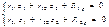
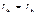
Определение коэф при неизвестных: 2 способа : 1) статический 2) общий (основанный на применении теорема о взаимности работ)
1. Выбор основной системы метода перемещ.
2. Построение эпюр изгиб моментов в основ системе метода перемещ от единичн смещений и от внеш нагрузки.
Поскольку коэф свобод членов канон ур-ний явл реакциями связей основ системы, то они опред из уравн-ий равновесия.
Коэф представ реактив момент во введ заделках опредл из уравн равновес вырезанного узла. Коэф представл реактив усилия в дополн стержнях опред из условия равновес всех факторов действ на отсечен часть рамы
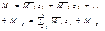
Общий способ применим к любой системе и позвол путем перемнож эпюрполучить формулы для реакций в общем виде.
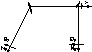
10 Динамический расчет системы
Этот расчет можно производить используя как МС так и МП
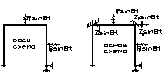
Основ сист задается путем наложения связей с одноврем динам неизвестн перемещ.
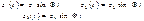
Канонич уравн-я
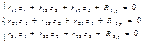
Неизвестные z1, z2, z3 – амплитуды вибрац перемещ. Коэф неизвестн-х – это амплитудные реакции связей от вибрационной нагрузки(т е при их определении учит силы инерции сосредоточенных или равномернораспред масс, стержней рамы). Для решения таких задач использ спец значения таких функций зависят от аргумента u 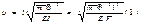
Где l – длина стержня, 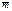 - погонная масса стержня, EI- жесткость стержня,
- погонная масса стержня, EI- жесткость стержня, 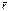 - пол. жест. стер. q - частота вынужденных колебаний=частоте возмущ сил. При рассм собств колеб в формулу 1 вместо q®w (частота собственных колеб) В канон уравн свобод члены равны 0. Для получения Ур-я частот заставляют, прирав к 0 и раскрыв-ся определитель, сост-ий из клэф-ов при неизвестных канон уравн-ий. Окончат эпюра строиться по формуле
- пол. жест. стер. q - частота вынужденных колебаний=частоте возмущ сил. При рассм собств колеб в формулу 1 вместо q®w (частота собственных колеб) В канон уравн свобод члены равны 0. Для получения Ур-я частот заставляют, прирав к 0 и раскрыв-ся определитель, сост-ий из клэф-ов при неизвестных канон уравн-ий. Окончат эпюра строиться по формуле 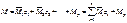
Расчет по МС:
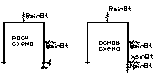
На сист действ вибрац гармонич нагрузки, q=const и наход в одной фазе. Заменим отброш связи неизвестн динамич реакциями, к-ые так же будут изменятся по тому же гармон закону к-му следует начальн нагр.
Канонич ур-ие, сокращаем sinqt
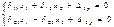
Где 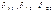 амплитудные значения перемещений по направл неизвест от динам силы.
амплитудные значения перемещений по направл неизвест от динам силы. 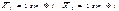
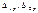 - амплитудные перемещпо направл неизвест сил от динам нагрузки. Коэф при неизвест и свобод члены канон ур опред по формуле
- амплитудные перемещпо направл неизвест сил от динам нагрузки. Коэф при неизвест и свобод члены канон ур опред по формуле
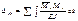 где
где 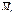 - выражает момент от силы
- выражает момент от силы 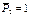 ,
, 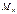 -выраж изгиб момент, от динам нагрузки с учетом сил инерции, т к возник трудности с опред Мизг от динам нагрузки с учетом сил инерции, то МС мало эффект для динам рсчета рам. Для определ частот рсвобод колеб рам свобод члены канон ур приним =0, а вместо q берется w неизвест частот свобод колеб. Определитель из коэф системы прирав 0 и раскрывают. Это последнее уравн трансцендентное и сложное.Единств способ его нахожд – подбор.
-выраж изгиб момент, от динам нагрузки с учетом сил инерции, т к возник трудности с опред Мизг от динам нагрузки с учетом сил инерции, то МС мало эффект для динам рсчета рам. Для определ частот рсвобод колеб рам свобод члены канон ур приним =0, а вместо q берется w неизвест частот свобод колеб. Определитель из коэф системы прирав 0 и раскрывают. Это последнее уравн трансцендентное и сложное.Единств способ его нахожд – подбор.
6. Основные формы потери устойчивости
При потере устойчивости формы наруш условия равновесия между внеш и внутр силами, соответст первоначальному виду деформации. Потерю уст, связанную с разветвлением форм равновесия, назыв потерей устойчивости I-ого рода. Хаар-ся при постепенном возраст нагрузки, разрушение прежней формы деф-ции, качественно отличное от прежней. К таким нарушениям относятся:
1. Потеря устойчивости центра сжатия
2. Потеря уст симметрии формы деформации
3. Потеря уст плоской формы и изгиба.
Потеря устойчивости плоской формы изгиба. Предельное значение нагрузки, при к-ых становятся возможными возникновение деформаций нового типа называется критической для заданного сооружения. Состояние сооруж при к-ом происходит потеря уст прежней формы деформ наз критич состоянием первого рода.
Рост деформ при отсутствии приращения нагрузки рассм как потеря уст II-ого рода, связанная с потерей несущей способности сооруж. Предельные значения нагрузки, при к-ом деформ увелич без приращения нагрузки наз критич нагрузкой при потере утс II рода. Потеря уст Iого и IIого рода как при упругих деформ. так и при работе сооружения за пределами упругости.
30. Степень свободы в динамике сооружений.
Степень свободы – это число независимых координат, определяющих положение масс движ вместе с сист всевозмож упругих и упругопластич перемещениях в сист-х. Чмсло степеней свободы удобно определять как число связей, к-ые надо приложить на сист, чтобы её массы наход в покое.

Сист с бесконеч числом степ своб можно приводить к сист с конечн числом степ своб путем дискре-и
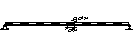
Число участков =¥Þчисло степ свободы=¥.
Абсолютно жесткий стержень. Ст. своб такой сист с прикрепл точечными массами будет определяться одной коор-ой, к-ой будет угол поворота
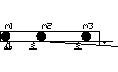
Плоская рама
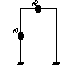 Масса m1 имеет 1 ст свобожы, масса m2 прикрепл к ригелю и может смещаться по вертикали и горизонтали, соотв m2 имеет 2 ст свободы. В сумме рама имеет 3 ст свободы.
Масса m1 имеет 1 ст свобожы, масса m2 прикрепл к ригелю и может смещаться по вертикали и горизонтали, соотв m2 имеет 2 ст свободы. В сумме рама имеет 3 ст свободы.








