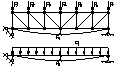
21 Определение частоты колебаний балочной фермы
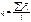 /
/
Способ перехода к эквивалентной балки состоит в том, что ферма заменяется балкой сплошного сечения, обладающей жесткостью эквивалентной жесткости фермы и тогда частота колебаний фермы определяется как для балки.
Момент инерции искомой балки определяется из условия равенства прогибов фермы и эквивалентной балке в наибольшей характерной точке – в середине пролета или над точкой приложения наибольшего сосредоточенного груза.
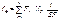 ,
, 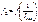 ,
, 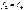
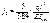
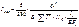
Зная моменты инерции эквивалентной балки можно определить частоту колебаний фермы по формуле:
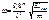 ,
, 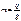 ,
,
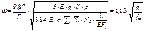
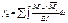 ,
,
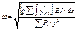 ,
, 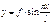 ,
,
Используемые приемы перехода к эквивалентной балки для определения частот колебаний фермы дают удовлетворительные результаты.
24. Устройство стержня с жёсткой заделкой на одном конце и упругой опорой ан другом.
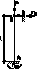 Т.к.
Т.к. 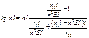
и 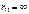 , а
, а 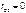 получаем
получаем
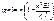 откуда:
откуда:
1) при r11=0 (свободный верхний конец) получим 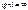 ,
, 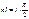 (где i=1,2,3…) и
(где i=1,2,3…) и 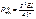
2) При 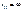 (жёсткий опорный стержень)
(жёсткий опорный стержень) 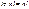
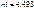
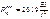
45. Определение коэффицентов при неизвестных метода сил.
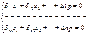
Коэффициенты при неизвестных 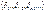 являются переменными основной системы по направлению неизвестных от единичных сил
являются переменными основной системы по направлению неизвестных от единичных сил 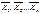 действующих по направлению неизвестных Х1, Х2,…Хn. Свободные члены уравнений
действующих по направлению неизвестных Х1, Х2,…Хn. Свободные члены уравнений 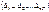 - это переменные основной системы по направлению неизвестной от заданной нагрузки.
- это переменные основной системы по направлению неизвестной от заданной нагрузки.
Коэффициенты при неизвестных и свободных членах уравнений определяют с помощью интеграла Максвелла-Мора:
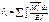
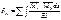
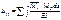
Предворительно должны быть построены эпюры моментов от единичных нагрузок (сил) и от заданной нагрузки. Где возможно применяют правило Верещагина. Главные коэффициенты 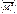 всегда положительны, а побочные
всегда положительны, а побочные 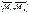 - положительны, отрицательны и равны 0.
- положительны, отрицательны и равны 0.
В основной системе как можно большее число побочных перемещений должно быть равно нулю!
4. Энергетический метод исследования устойчивости.
Основан на исследовании энергетических признаков устойчивого и не устойчивого равновесия упругой системы, согласно которым система находится в состоянии устойчивого равновесия, если её потенциальная энергия минимальна по сравнению с энергией смежных равновесных систем.
Если 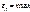 , то равновесие устойчиво.
, то равновесие устойчиво.
Пример: Определить Ркр для жёсткого стержня.
Выразим изменения упругой энергии системы через работу силы Р. Работа силы:
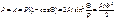
Работа совершаемая опорным моментом, определяется:
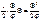
Изменение полной упругой энергии:
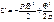
Энергетическим критерием потери устойчивости системы является условие:
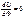
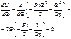
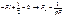
44. Учёт сил сопротивления при вынужденных колебаниях. Резонанс. Коэффициент динамичности.
При вынужденных колебаниях на систему кроме сил инерции и сил сопротивления действует сила P(t):
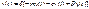
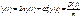
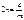
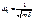
Общее решение уравнения:
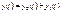
Где 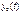 - общее решение однородного уравнения;
- общее решение однородного уравнения; 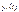 - частное решение неоднородного уравнения.
- частное решение неоднородного уравнения.
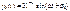
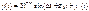
K - динамический коэффициент:
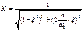
Где 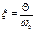 - относительная частота.
- относительная частота.
При совпадении частот вынужденных колебаний 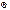 и частот собственных колебаний
и частот собственных колебаний 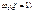 возникает резонанс и при n=0 динамический коэффициент стремится к бесконечности. Явление резонанса при действии периодических сил может привести к разрушению конструкции, поэтому при действии на конструкцию периодических сил с частотой
возникает резонанс и при n=0 динамический коэффициент стремится к бесконечности. Явление резонанса при действии периодических сил может привести к разрушению конструкции, поэтому при действии на конструкцию периодических сил с частотой 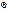 необходимо проверять, насколько близка эта частота к частоте свободных колебаний
необходимо проверять, насколько близка эта частота к частоте свободных колебаний 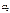 .
.
11. Применение уравнений 3-х моментов для расчёта неразрезных балок.
В качестве основной системы необходимо взять систему разрезных балок, полученную из заданной системы включением шарниров в опорные сечения. За неизвестное примем опорный изгиб. Моменты, очевидно, что число их равно числу промежуточных опор при наличии крайних шарнирных опор. Решение выбранной основной системы заключается в том, что эпюры моментов от единичных усилий распространяются в ней только на два соседних пролёта и значит, большое число побочных перемещений обращается в ноль. Для составления типового канонического уравнения в развёрнутом виде строим эпюры изгибающих моментов в основной системе от внешней нагрузки и единичных усилий. Из рассмотрения этих эпюр вытекает, что типовые канонические уравнения будет трёхчлен следующего вида:
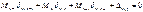
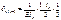
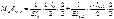
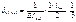
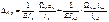
Подставляем: ……
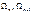 - площади эпюр моментов;
- площади эпюр моментов;
an , bn+1 – расстояние от центров тяжести этих эпюр. Умножим правую и левую части на 6EIc получаем:
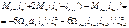
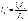
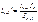
Уравнение 3-х моментов в общем виде. Если I=const
В уравнениях неизвестными являются 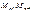 т.е. для расчёта неразрезной балки необходимо составить столько уравнений трёх моментов, сколько промежуточных опор, решая совместно внешним силам.
т.е. для расчёта неразрезной балки необходимо составить столько уравнений трёх моментов, сколько промежуточных опор, решая совместно внешним силам.
Если конец защемлён, для применения уравнения трёх моментов вводим дополнитьельный фиктивный пролёт. Для опоры ‘o’ составляем уравнения:
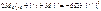
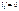
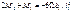
При отсутствии внешней нагрузки на крайнем 1-м пролёте у защемлённого конца: 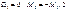
42. Решение системы ДУ с конечным числом степеней свободы. Вековое уравнение.
Рассмотрим балку несущую n сосредоточенных масс, совершающих свободные колебания в вертикальной плоскости. 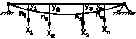 Число степеней свободы = n. Х1, Х2, Х3 … Хn – силы инерции; у1, у2, у3 … уn – отклонение масс; А1, А2, А3 … Аn – амплитуды.
Число степеней свободы = n. Х1, Х2, Х3 … Хn – силы инерции; у1, у2, у3 … уn – отклонение масс; А1, А2, А3 … Аn – амплитуды.
Уравнения движения масс:
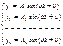
Сила инерции К – ой массы:
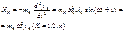
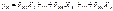
Подставим:
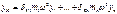
Разделим всё на 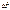 и обозначим
и обозначим 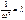 ;
;
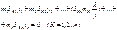
Система уравнений будет выглядеть:
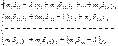
Эта система уравнений имеет не нулевое решение , если определитель составленный из коэффициентов при енизвестных у1…уn.
Вековое уравнение:
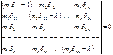
Раскрываем определитель и получаем полином степени n относительно 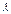
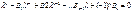
Все корни этого уравнения положительны и у всех своя частота:
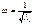 ;
; 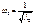 …
… 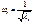 .
.
Совокупность частот – спектр.
Систему уравнений можно записать в математическом виде (вековое уравнение) 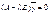 , где
, где
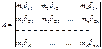 ;
;
Е – единичная матрица.
Решение с числом степеней свободы более 2 – 3 затруднительно.
49. Основы динамики сооружений. Основные понятия. Типы нагрузок.
Динамика сооружений занимается разработкой принципов и методов расчёта сооружений на действие динамических нагрузок.
Динамические нагрузки – это такие нагрузки величина, направление и положение которых изменяется во времени. При действии на сооружение таких нагрузок, возникают и играют существенную роль силы инерции масс этих нагрузок и самого сооружения. Все динамические нагрузки вызывают колебания конструкции на которые они действуют.
Динамический расчёт производится как для проверки сооружения на прочность, так и для определения величин динамических перемещений, скоростей и ускорений, которые действуют на людей и на некоторые виды оборудования (измерительные приборы).
Динамические нагрузки разделяют:
1. Периодическая – создаваемая стационарными машинами, станками и т.п., т.е. приборами с движущимися частями. Нагрузки такого вида не зависят от свойств конструкции на которые они воздействуют, но являются основным источником колебаний этих конструкций.
2. Импульсивная – создаваемая падающими грузами и падающим частями силовых установок (молотов, копров и т.д.). Эти нагрузки характеризуются небольшой продолжительностью действия и зависит от упругих и инерциальных свойств конструкций, воспринимающих удар.
3. Подвижная – положение которой в пролётахсооружения изменяется во времени (нагрузка от подвижного состава ж.д., автотранспорта, кранов и т.д.).
Динамические нагрузки могут быть комбинированными (импульсивно-переодическими от копров переодического действия).
К динамическим нагрузкам относят ветровые, сейсмические и прочее.
Для решения задач динамики используют два основных способа:
· Статический – основанный на применении уравнений динамического равновесия, которые отличаются от уравнений статического равновесия дополнительным учётом сил инерции в виде произведения масс или их моментов инерции на ускорения, т.е. на вторую производную линейных или угловых перемещений во времени.
· Энергетический – основанный на применении закона сохранения энергии, согласно которому сумма потенциальных энергии и кинетической энергии упругой системы является величиной постоянной во времени.
Трудоёмкость динамического расчёта системы зависит от степени свободы системы. При определении степени свободы в динамике сооружений рассматривают её упругие или упругопластические деформации.
22. Общие свойства статически неопределимых систем. Степень статической неопределимости. Основная система метода сил.
Статически неопределимая система – это система, определение усилий в которой невозможно с помощью одних лишь уравнений статики.
Сооружения могут быть неопределимыми по своему внутреннему образованию. В этом случае определимость называется внутренней. Распределение усилий в таких системах зависит не только от внешних сил, но и от соотношений между поперечными размерами отдельных элементов, а также от модулей упругости этих материалов. Другая особенность – смещение опор, to-ые воздействия и неточность сборки конструкций обычно вызывают появление доп. Усилий, в отличии от сат. опред. систем. Разность между числом неизвестных усилий в сооружении и числом независимых уравнений статики, к-е можно составить при расчетах этого сооружения, определяет степень его статической неопределимости. Сущность метода сил заключается в том, что заданная статически неопределимая система (ее расчет) заменяется расчетом эквивалентной ей статически опред-ой системы. Для получения эквивалентной системы необходимо прежде всего получить так называемую осн. систему. Для этого из заданной стат. неопред-ой системы удаляют все лишние связи, число их естественно равно степени стат. неопред-ти. Число лишних связей или степень стат. Неопределимости будем опред-ть по ф-ле: n=3K-Ш-2П. Для превращения осн. сис-мы в эквивалентную заданной необходимо приложить к ней все заданные нагрузки, приложить реакции всех удаленных связей (Х1, Х2, Х3). Составляем уравнения совместимости перемещений по направлению каждой линией связи. Определив все коэ-ты при неизвестных и свободные члены уравнений совместимости перемещений, решаем систему этих уравнений. 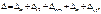 где слагаемое Δ1к – перемещение по направлению связи i, вызванное действием реакции связи k. Слагаемое Δip – означает перемещение по направлению связи i, вызванное действием заданной нагрузки. Затем находим лишние неизвестные, после чего строим эпюры M,Q,N.
где слагаемое Δ1к – перемещение по направлению связи i, вызванное действием реакции связи k. Слагаемое Δip – означает перемещение по направлению связи i, вызванное действием заданной нагрузки. Затем находим лишние неизвестные, после чего строим эпюры M,Q,N.
35. Приближенные способы определения частот свободных колебаний. Энергетический способ.
Приближение точных приемов для систем с числом степеней свободы более 3-х связаны с громоздкими вычислениями, к-е значительно усложняется при учете собственного веса. Это обстоятельство заставляет прибегать к применению приближенных способов определения частот. Во многих задачах определение всех частот оказывается излишним и достаточно определить первую наименьшую частоту колебаний. Это возможно только в том случае, если частота собственных колебаний больше частоты возмущающей нагрузки и следовательно резонанс с более высокими частотами не возможен. Для отыскания 1-й частоты могут быть использованы приближ. способы:
-способ приведенных масс;
-замены распределенных масс – сосредоточенными;
-энергетический способ.
Энергетический способ:
В его основу положен закон сохранения энергии: при колебаниях системы в любой момент времени сумма кинетических и потенциальных энергий останься постоянной: U+V=const.

U=0 V=max Qmax U=max V=0 Qmin=0
Umax=Vmax (1)
Если форма колебаний, т.е. вид упругой деформации был бы нам известен заранее, то ур-е (1) привело бы к строгому решению. Для приближенного решения задачи можно задать форму стоящей волны: y=f(x), к-е удовлетворяло бы граничным условиям:
y(x,t)=y(x)sin(ωt+φ0) (2)
y΄(x,t)=v(x)=y(x)ωcos(ωt+φ0) (3)
при cos(ωt+φ0)=1 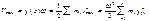 (4)
(4)
Потенциальная энергия по ур-ю Клайперона: 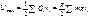 (5)
(5) 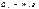
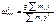 (6). Если на систему действуют распределенные массы, то формула (6) предст-ся в виде:
(6). Если на систему действуют распределенные массы, то формула (6) предст-ся в виде: 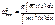 (7) Если масса
(7) Если масса 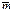 =const
=const 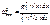 . При пост.
. При пост. 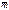 по длине балки получаем в числитель, представляющий собой эпюру прогибов. В качестве ф-ции y(x) можно брать любую кривую, к-ая удов-ет граничным условиям – кривую соотв-ю стат-му напряжению (полуволну синусоиды).
по длине балки получаем в числитель, представляющий собой эпюру прогибов. В качестве ф-ции y(x) можно брать любую кривую, к-ая удов-ет граничным условиям – кривую соотв-ю стат-му напряжению (полуволну синусоиды).
7. Определение перемещений в стат-ки опред. сист-ах от осадки опор.
Перемещения от случайных осадок опор. Осадки опор могут быть случайными вызванными просадкой грунта, размывом, оползнем и др. причинами). При отсутствии нагрузки на сооружение осадки могут возникнуть под действием нагрузки в рез-те податливости основания. Рассматривая первый случай будем считать, что 3-х шарнирная арка получает одинаковые горизонтальные смещения опор ΔH и верт. смещение левой опоры Δа , причем величины смещений зданий от действующих осадок опор в стат. опред. системах внутр. усилия не возникают. Часто необходимо определить новое положение системы. Пусть нужно найти вертик. и гориз. перемещения ключевого шарнира с. Для определения верт. перемещения по ф-ле Мора представим един. сост. действ. вертик. силы 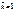 . Составим сумму работ: 1∙Δy-VaΔa-HΔH-HΔH=0 Δy= VaΔa+2HΔa. Для определения Δx 1∙Δx-V΄aΔa-H΄ΔH-H΄ΔH=0 Δx= V΄aΔa.
. Составим сумму работ: 1∙Δy-VaΔa-HΔH-HΔH=0 Δy= VaΔa+2HΔa. Для определения Δx 1∙Δx-V΄aΔa-H΄ΔH-H΄ΔH=0 Δx= V΄aΔa.
Перемещения от нагрузки вызыв. упругие осадки. Чаще всего в практике осадки опор возникают в рез-те действия нагрузки при наличии упругой податливости грунтов. Пусть под действием нагрузки 3-х шарнирная рама получает равные верт. осадки опор: Δ=VA/k0, где k0 – коэф-т оседания опоры. Найдем верт. перемещения ключевого шарнира, учитывая при этом только влияние изгибающих моментов Мр.
Представляя ед. состояние действия силы k=1, приложенной к ключевому шарниру с , применяется теорема Мора к внеш. и внутр. силам этого состояния, принимая за возможные перемещения в действ. сост. Тогда получаем: 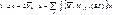 откуда
откуда 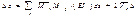 т.о. перемещения нагр. соор-я при наличии осадок опор вычисляют возможную работу внутр. сил ед. сост. на перемещениях действительном состоянии и возможную работу реакций ед. состояния.
т.о. перемещения нагр. соор-я при наличии осадок опор вычисляют возможную работу внутр. сил ед. сост. на перемещениях действительном состоянии и возможную работу реакций ед. состояния.
8. Динамический расчет системы методом перемещений.
Порядок расчета:
1. Анализируем схему и выбираем основную систему.
2. Строится изгибающий момент.
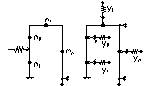
Для заданной системы основная получилась путем введения связей по направлению неизвестных перемещений z1, z2 … zn cсоответствующих масс m1, m2 …mn. число степеней свободы упругой системы определяется числом возможных независимых смещений. Получаем систему уравнений: 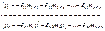 (1)
(1)
Частное решение системы:
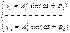 (2)
(2)
A1, An – амплитуды колебаний соотв. масс, φ0 – нач. фаза колебаний.
Возьмем вторую производную по времени t:
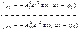 (3)
(3)
Подставляем из ур-я (3) и (2)в (1):
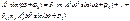
Перобразовываем:
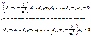
1/ω2=λ
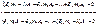
Если А1=А2=…=Аn=0 (сист-ма наход. в покое) Если А1≠А2≠Аn, тогда когда определитель из коэф-ов при амплитудах=0.
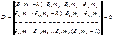
Вековое ур-ие с n-степенью свободы.
Раскрываем полученный определитель. Если вековое уравнение 2-го или 3-го порядка его решение достаточно просто, но при дальнейшем увеличении порядка решение становится затруднительным.
59. Устойчивость кругового кольца при гидростатич. давлении.
До потери устойчивости все сечения кольца испытывают только сжатие и продольная сила равна N=qR. При достижении нагрузкой критического значения может произойти потеря устойчивости и кольцо примет слегка изогнутую форму, к-ая будет формой равновесия. Рассмотрим изогнутую равновесную форму с двумя осями симметрии. ДУ изгиба бруса кругового очертания: 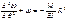 . Изгибающий момент в точке А΄ равен M0=qRω0, а изгиб. момент в произвольной точке kM=qRω. Подставляя в ДУ и после небольшого преобразования.
. Изгибающий момент в точке А΄ равен M0=qRω0, а изгиб. момент в произвольной точке kM=qRω. Подставляя в ДУ и после небольшого преобразования. 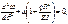 обозначив через
обозначив через 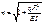 получим общее решение этого однородного диф. уравнения в след. виде.
получим общее решение этого однородного диф. уравнения в след. виде. 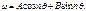
Граничные условия:
1) при θ=0 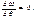
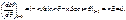 откуда B=0;
откуда B=0;
2) при 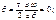
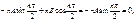
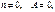 т.к. ω не обращается тождественно в ноль, следовательно,
т.к. ω не обращается тождественно в ноль, следовательно, 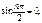 что дает минимальное значение nmin=2. Таким образом, минимальная критическая нагрузка, соответ. данной форме потери устойчивости, определяется из условия
что дает минимальное значение nmin=2. Таким образом, минимальная критическая нагрузка, соответ. данной форме потери устойчивости, определяется из условия 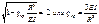 .
.
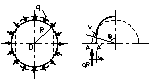
6. Метод исследования устойчивости упругих систем .
В задачах устойчивости используют энергетический и статический метод (есть еще динамический, но он редко применяется). Статический метод – заключается в составлении и интегрировании ДУ равновесия элемента упругой системы, находящейся в таком деформированном состоянии, к-ое отличается от исходного наличием перемещений, вызывающих новый вид деформации.
Энергетический метод – основан на использовании энергетических признаков устойчивого и неустойчивого равновесия упругой системы, согласно к-м система находится состоянии устойчивого равновесия, если ее потенциальная энергия минимальна по сравнению с энергией смежных равновесных. Если εр=max, то равновесие устойчиво.
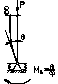
Пример: Определить Ркр для жесткого стержня. М=1; φ=1 – угол поворота. Стат. метод: ΣМА=0 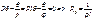 .
.
Энергетический метод: Выразим изменения упругой системы через работу силы Р. Работа силы Р=А=Pl(1-cosθ)=2Plsin2 (θ/φ)=(Plθ2)/2. Работа совершаемая опорным моментом, определяется 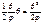 . Изменение полной упругой энергии
. Изменение полной упругой энергии 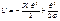 . Энергетическим критерием потери устойчивости системы явл. условие:
. Энергетическим критерием потери устойчивости системы явл. условие: 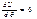
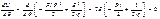
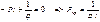 .
.
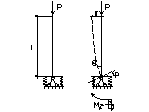
20. Расчет рам комбинированным способом.
Сущность комбинированного приема расчета поясним на примере рамы, изображенной на рис. 7.59. Раскладывая действующую на нее несимметричную нагрузку на симметричное и обратносимметричное воздействия, получим два состояния рамы, изображенные на рис. 7.60, а, б. Для каждого из этих состояний можно легко
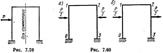
установить число неизвестных при расчете рамы методом сил и методом перемещений. Так, из симметрии деформации рамы при симметричном ее загружении следует, что смещение ригеля /—2 по горизонтали равно нулю, а поворот узла 1 равен повороту узла 2 и противоположен ему по направлению, т. е.Z 3 =0, a Z 1 = Z 3 (рис. 7.61, а).
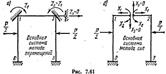
Следовательно, рассчитывая раму методом перемещений на симметричную нагрузку, необходимо составить и решить одно уравнение с одним неизвестным. Применяя же для этого метод сил и используя основную систему, изображенную на рис. 7.61, б, а также учитывая при этом, что поперечная сила X 3 при симметричном загружении рамы равна нулю, придется составить и решить два уравнения с двумя неизвестными.
Очевидно, что на симметричную составляющую заданной нагрузки целесообразно рассчитать рассматриваемую раму методом перемещений.
Основная система метода перемещений при воздействии на раму обратносимметричной нагрузки изображена на рис. 7.62, а. Число неизвестных равно двум. В самом деле, углы поворота узлов 1 и 2 (учитывая обратносимметричный вид нагрузки) будут как по величине, так и по направлению равны друг другу; ригель же 1—2 получит горизонтальное, смещение, т. е.Z 3 ≠0.








