5.5.3. Заполните таблицу 2.2, колонку «Эксперимент» для цепи RC.
5.6. Определите изменение амплитуды от частоты (снимите АЧХ последовательной RC цепи.) с помощью функционального генератора и вольтметра.
5.6.1. Откройте окна функционального генератора (FGEN) и цифрового мультиметра (DMM).
5.6.2. В окне цифрового мультиметра, переключитесь в режим измерения переменного напряжения.
5.6.3. Установите на генераторе амплитуду 5 В.
5.6.3. Изменяя частоту сигнала в окне функционального генератора, запишите в таблицу 2.2 измеренное переменное напряжение на резисторе. Частоты брать точно такие же, какие записаны в случаи измерения ФЧХ.
5.7. На макетной плате соберите схему для исследования последовательной RL цепи. Для этого замените в цепи RC конденсатор на катушку индуктивности. Повторите измерения и заполните таблицу 2.2, колонку «Эксперимент» для цепи RL.
5.8. На макетной плате соберите схему для исследования последовательной RLС цепи. Для этого в цепи RL между L и R должен быть установлен конденсатор. Повторите измерения и заполните таблицу 2.2, колонку «Эксперимент» для цепи RLС. ПРИМЕЧАНИЕ: после сборки схемы, проверьте правильность подключения анализатора ФЧХ и вольтметра. Анализатор должен подключаться одним входом до реактивных элементов (между генератором и катушкой), вторым после (между конденсатором и резистором). Вольтметр должен подключаться параллельно резистору. (НАРИСОВАТЬ СХЕМУ!!!)
5.9. По экспериментальным данным таблицы 2.2, постройте векторные диаграммы для частот f1=2кГц, f2=8кГц.
6. Содержание отчета
6.1. Название и цель работы.
6.2. Заполненные таблицы 2.1 и 2.2
6.3. Расчетная часть в соответствии с пунктом 4.5.
6.4. Схемы измерения в соответствии с пунктами 5.1, 5.5 – 5.8 с указанием координат гнезд, которые использовались для сборки схемы.
6.5. Графики АЧХ и ФЧХ в соответствии с показаниями таблицы 2.2.
6.6. Векторные диаграммы в соответствии с пунктом 5.9.
6.7. Вывод по работе.
6.8. Ответы по допуску к работе.
6.9. Ответы на контрольные вопросы.
Таблица 2.2.
| Цепь | RL | RC | RLC | ||||||||||
| Тип данных | Расчет | Экспери мент | Расчет | Эксперимент | Расчет | Экспери мент | |||||||
| Um , В | φ | Um , В | φ | Um , В | φ | Um , В | φ | Um , В | φ | Um , В | φ | ||
| Частота воздействия, кГц | 2 | ||||||||||||
| 4 | |||||||||||||
| 6 | |||||||||||||
| 8 | |||||||||||||
| 10 | |||||||||||||
| 12 | |||||||||||||
| 14 | |||||||||||||
| 16 | |||||||||||||
7. Контрольные вопросы
7.1. Что такое АЧХ?
7.2. Что такое ФЧХ?
7.3. Для чего нужен анализатор АЧХ и ФЧХ?
7.4. Какие параметры необходимо задать, что бы снять АЧХ и ФЧХ с помощью анализатора?
7.5. От чего зависит точность измерения, при использовании анализатора АЧХ и ФЧХ?
7.6. Для чего на анализаторе АЧХ и ФЧХ настраиваются два канала? Для чего они нужны?
7.7. От куда берется сигнал воздействия на входе схемы измерения, если окно функционального генератора не запускается и сигнал не настраивается?
8. Приложение
Применение метода комплексных амплитуд для расчета линейных электрических цепей основано на их свойстве сохранять неизменными форму и частоту воздействующего гармонического колебания.
Так, если к цепи приложено напряжение
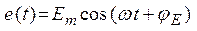 (2.1)
(2.1)
то напряжение и ток на k-м элементе цепи также будут гармоническими функциями
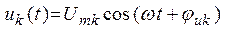 , (2.2)
, (2.2)
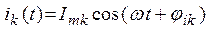 (2.3)
(2.3)
Неизвестными при этом являются только амплитуды 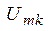 ,
, 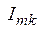 и начальные фазы
и начальные фазы 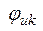 ,
, 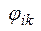 . Используя свойство суперпозиции, можно анализировать прохождение через линейную цепь не заданного сигнала (2.1), а комплексной функции
. Используя свойство суперпозиции, можно анализировать прохождение через линейную цепь не заданного сигнала (2.1), а комплексной функции 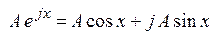 , реальная часть которой равняется исходному воздействию
, реальная часть которой равняется исходному воздействию 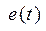 . При этом выходной сигнал является суперпозицией откликов на составляющие входного воздействия из которого можно выделить реальную часть – отклик на
. При этом выходной сигнал является суперпозицией откликов на составляющие входного воздействия из которого можно выделить реальную часть – отклик на 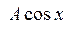 . Таким образом, представляя входное воздействие в виде функции
. Таким образом, представляя входное воздействие в виде функции 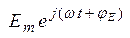 - вектора, вращающегося на комплексной плоскости с частотой
- вектора, вращающегося на комплексной плоскости с частотой 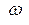 , выходной сигнал (напряжение на k-м элементе) получим в виде
, выходной сигнал (напряжение на k-м элементе) получим в виде 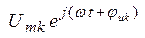 , реальная часть которого соответствует искомому напряжению
, реальная часть которого соответствует искомому напряжению 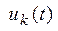 . Принимая во внимание, что входной и выходной векторы вращаются с одинаковой частотой, можно перейти к неподвижным векторам
. Принимая во внимание, что входной и выходной векторы вращаются с одинаковой частотой, можно перейти к неподвижным векторам 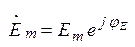 и
и 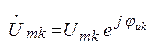 . Это комплексные числа, которые содержат информацию об амплитуде и начальной фазе гармонических функций и называются комплексными амплитудами.
. Это комплексные числа, которые содержат информацию об амплитуде и начальной фазе гармонических функций и называются комплексными амплитудами.
Для комплексных амплитуд напряжений и токов справедливы законы Ома и Кирхгофа. При этом вводятся понятия комплексных сопротивлений для резистора 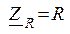 , индуктивности
, индуктивности 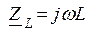 и емкости
и емкости 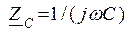 . Комплексные проводимости равны обратным величинам комплексных сопротивлений
. Комплексные проводимости равны обратным величинам комплексных сопротивлений 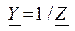 .
.
При последовательном соединении элементов суммируются их комплексные сопротивления 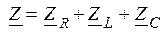 , а при параллельном – их комплексные проводимости
, а при параллельном – их комплексные проводимости 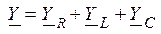 . Законы Ома и Кирхгофа в комплексной форме имеют следующий вид:
. Законы Ома и Кирхгофа в комплексной форме имеют следующий вид:
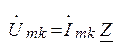 ;
; 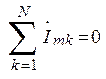 ;
; 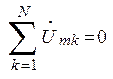 . (2.4)
. (2.4)
Знак перед ЭДС в последнем выражении выбирается “+“, если направление тока в контуре совпадает с направлением ЭДС и “-”, если не совпадает.
В общем виде комплексная амплитуда выходного напряжения или тока является комплексной функцией частоты входного воздействия.
Зависимость отношения комплексных амплитуд отклика к постоянному по амплитуде (действующему значению) воздействию от частоты называется комплексной частотной характеристикой цепи (КЧХ):
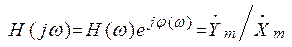 . (2.5)
. (2.5)
Здесь 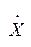 - комплексная амплитуда входного, а
- комплексная амплитуда входного, а 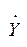 - выходного напряжения или тока.
- выходного напряжения или тока.
Комплексная частотная характеристика не зависит от амплитуды и начальной фазы входного воздействия и является характеристикой цепи. Модуль КЧХ называется амплитудно-частотной характеристикой цепи (АЧХ):
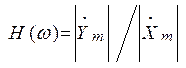 , (2.6)
, (2.6)
а ее аргумент – фазо-частотной характеристикой (ФЧХ):
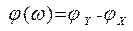 (2.7)
(2.7)
При анализе энергетических процессов в электрических цепях вводятся понятия полной 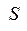 , активной
, активной 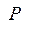 и реактивной
и реактивной 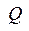 мощностей:
мощностей:
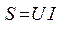 ,
, 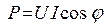 ,
, 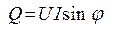 , (2.8)
, (2.8)
где 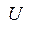 и
и 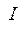 - действующие значения напряжения и тока, а
- действующие значения напряжения и тока, а 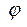 - фазовый сдвиг между ними. Указанные мощности характеризуют скорость преобразования энергии источника и соответствуют различным ее составляющим. Активная мощность характеризует ту часть электрической энергии источника, которая преобразуется цепью в другие виды энергии, реактивная характеризует обмен энергией между цепью и источником, а полная – общую энергию, потребляемую цепью.
- фазовый сдвиг между ними. Указанные мощности характеризуют скорость преобразования энергии источника и соответствуют различным ее составляющим. Активная мощность характеризует ту часть электрической энергии источника, которая преобразуется цепью в другие виды энергии, реактивная характеризует обмен энергией между цепью и источником, а полная – общую энергию, потребляемую цепью.








