Тема 3. Погрешности измерений и средств измерений

Дата: 2025-05-01; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

3.1 Погрешности измерений

Отклонение результата измере­ния от истинного значения измеряемой величины называется погреш­ностью измерения. Различают абсолютные погрешности измерения, ко­торые выражаются в единицах измеряемой величины, и относительные погрешности измерения, определяемые как отношение абсолютной по­грешности измерения к значению измеряемой величины:

Δ = х – х_и; (3.1)

δ = Δ/х, (3.2)

где Δ - абсолютная погрешность измерения; х - значение, полученное при измерении; х_и - истинное значение измеряемой величины; δ - относительная погрешность измерения.

Абсолютная погрешность Δ является резуль­тирующей погрешностью, т.е. суммой систематической Δ_с и случайной Δ₀ погрешностей.

Систематической погрешностью измерения называется составляющая погрешности измерения, остающаяся постоянной или закономерно изме­няющаяся при повторных измерениях одной и той же величины (неисправности измерительной аппаратуры, несовершенство метода измерений, неправильная установка измерительных приборов и т.д.).

Случайной погрешностью измерения называется составляющая по­грешности измерения, изменяющаяся случайным образом при повтор­ных измерениях одной и той же величины. Часто случайные погрешности возникают из-за одновременного действия многих независимых причин, каждая из которых в отдельно­сти мало влияет на результат измерения.

Результат измерения, содержащий грубую погрешность (промах), следует выявить, исключить и не учитывать при дальнейшей статисти­ческой обработке.

Существуют некото­рые общие причины возникновения систематических погрешностей, в соответствии с которыми их подразделяют на методические, инструмен­тальные и субъективные.

Методические погрешности происходят от несовершенства метода измерения, использования упрощающих предположений и допущений при выводе применяемых формул, влияния измерительного прибора на объект измерения. Например, измерение температуры с помощью термопары может содержать методическую погрешность, вызванную нарушением температурного режима исследуемого объекта (вслед­ствие внесения термопары).

Инструментальные погрешности зависят от погрешностей применяе­мых средств измерения. Неточность градуировки, конструктивные несовершенства, изменения характеристик прибора в процессе эксплуа­тации и т.д. являются причинами инструментальных погрешностей.

Субъективные погрешности вызываются неправильными отсчетами показаний прибора оператором.

Систематические погрешности могут оставаться постоянными либо закономерно изменяться. В последнем случае их подразделяют на про­грессирующие (возрастающие или убывающие), периодические и из­меняющиеся по сложному закону. Обнаружение причин и источников систематических погрешностей позволяет принять меры к их устранению или исключению посредством введения поправки.

Поправкой называется значение величины, одноименной с измеряе­мой, которое нужно прибавить к полученному при измерении значению величины с целью исключения систематической погрешности.

В некоторых случаях используют поправочный множитель - число, на которое умножают результат измерения для исключения системати­ческой погрешности.

Согласно теория вероятностей слу­чайная величина наиболее полно характеризуется своим законом рас­пределения (или плотностью распределения) вероятностей. При измерении чаще всего встречается нормальная и равномерная плотность распределения случайной величины.

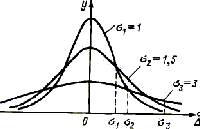Рисунок 3.1 – Нормальный закон распределения погрешностей

Нормальный закон распределения вероятностей имеет вид

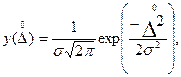(3.3)

где 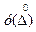- плотность вероятностей случайной погрешности 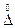; σ -среднее квадратическое значение случайной погрешности.

Кривые, соответствующие выражению (3.3) для разных значений σ, приведены на (рис.3.1). Очевидно, что при малых значениях σ получается погрешность измерений меньше, чем при больших.

Вероятность того, что погрешность результата измерения находится между заданными предельными значениям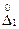и и 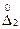вычисляется по формуле:

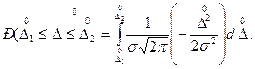(3.4)

Интеграл в формуле (3.4) вычисляется по таблицам функции Лапласа Ф(z).

Распределение погрешностей принимают равномерным, если

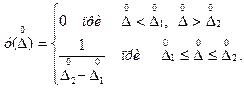(3.5)

Такой закон распределения характерен, например, для погрешностей отсчета по шкале прибора, погрешностей дискретности в цифровых измерительных приборах, погрешностей квантования в аналого-цифро­вых преобразователях (АЦП).

Поскольку истинное значение измеряемой величины х_и неизвестно, непосредственно случайную абсолютную погрешность Δ вычислить нельзя. При практических расчетах приходится вместо х_и использовать его оцен­ку. Обычно принимают, что истинное значение равно среднему арифме­тическому значению ряда измерений:

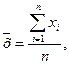
где x_i - результаты отдельных измерений; n - число измерений.

Введем важные понятия доверительной вероятности и доверитель­ного интервала. Среднее арифметическое зна­чение 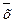, полученное в результате некоторого ряда измерений, является оценкой истинного значения х_и и, как правило, не совпадает с ним, а отличается на значение погрешности. Пусть Р_д есть вероятность того, что 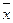отличается от х_и не более чем на Δ, т.е.

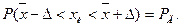(3.6)

Вероятность Р_д называется доверительной вероятностью, а интервал значений измеряемой величины от х – Δ до х + Δ - доверительным интервалом.

Приведенное выше равенство означает, что с вероятностью Р_д доверительный интервал от х - Δ до х + Δ заключает в себе истинное значение х_и.

Таким образом, чтобы характеризовать случайную погреш­ность достаточно полно, надо располагать двумя числами - доверитель­ной вероятностью и соответствующим ей доверительным интервалом. Если закон распределения вероятностей погрешностей известен, то по заданной доверительной вероятности можно определить доверительный интервал.

3.2 Погрешности средств измерений

Входной величиной измерительного прибора является его измеряемая величина. Наибольшее и наименьшее значения измеряемой величины, для которых нормированы погрешности, называются преде­лами измерения. Область значений, заключенная между верхним и нижним пределами измерения, называется диапазоном измерений. От диапазона измерений следует отличать диапазон показаний, который охватывает область значений шкалы, ограниченную конечным и началь­ным значениями шкалы.

Таким образом, диапазон измерений, охваты­вающий часть шкалы, в пределах которой измерения могут быть про­ведены с нормируемой погрешностью, более узок, чем диапазон показа­ний, охватывающий всю шкалу.

Функция преобразования - функциональная зависимость между выходной величиной у и входной величиной х. Желательно, чтобы функция преобразования была линейной.

Чувствительность - это отношение изменения выходной величины из­мерительного прибора к вызвав­шему ее изменению входной величины

S = dy/dx . (3.7)

Для прибора или преобразователя может определяться абсолютная, относительная и приведенная погрешности.

Абсолютная погрешность прибора в данной точке диапазона изме­рения равна

Δ = х_п - х, (3.8)

где х_п - показание прибора; х - истинное значение измеряемой ве­личины.

Однако в связи с тем, что истинное значение неизвестно, на практике вместо него используется действительное значение х_д. В ка­честве х_д принимают показания более точного, образцового прибора.

Относительная погрешность прибора равна отношению абсолютной погрешности к истинному значению измеряемой величины и обычно выражается в процентах:

δ = (Δ/х) • 100 = [(x_п - х)/х] 100. (3.9)

Приведенная погрешность прибора у также выражается в процентах и равна отношению абсолютной погрешности к нормирующему значе­нию x_N, которое принимается равным верхнему пределу измерений (если нулевая отметка находится на краю или вне шкалы) или диапазо­ну измерения (если нулевая отметка находится внутри диапазона изме­рений):

γ = (Δ/x_N) ∙ 100 = [(х_П - x)/x_N] 100. (3.10)

Значения абсолютной, относительной и приведенной погрешностей используются для нормирования погрешности приборов.

Обычно СИ имеют линейную функцию преобразования

у = S ∙ x + у₀, (3.11)

где S – чувствительность прибора; у₀ - значение выходной ве­личины при нулевом значении входной.

Отклонение такой функции преобразования от номинальной может быть вызвано отклонением у₀ и отклонением чувствительности S.

По­грешность, обусловленная неноминальным значением выходной вели­чины при нулевом значении входной у₀, называется аддитивной.

По­грешность, обусловленная неноминальным значением чувствительно­сти S, называется мультипликативной.

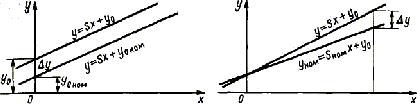
Аддитивная погрешность не зависит от входной величины. При изменении у₀ вследствие каких-либо причин график функции преобразования перемещается параллельно самому себе (рис.3.2,а).

Значение этой погрешности

Δу = Δу₀ = у₀ - у_0ном , (3.12)

где у_0ном — номинальное значение у₀.

При мультипликативной погрешности наклон прямой, графически отображающий функцию преобразования, отличается от наклона при номинальной функции преобразования (рис.3.1,б). При этом абсолютная погрешность Δу = у- у_ном зависит от входной величины х.

При изменении чувствительности на ΔS абсолютная погрешность преобразователя

Δу = ΔS ∙ х, (3.13)

т.е. абсолютная мультипликативная погрешность пропорциональна вход­ной величине х.

а) б)

Рисунок 3.2 – Погрешности: а) аддитивная; б) мультипликативная

Относительная мультипликативная погрешность равна

δ у = ΔS/S (3.14)

Относительная мультипликативная погрешность равна относительному изменению чувствительности.

Погрешность СИ зависит от условий проведения измерений. При этом различают основную и дополнительную погреш­ности.

Основной погрешностью называется погрешность, существующая при так называемых нормальных условиях, которые указаны в норма­тивных документах, регламентирующих правила испытания и эксплуа­тации данного средства измерения. Например, нормальные усло­вия считаются когда температура окружающей среды +20 ± 2°С; положение прибора горизонтальное с отклонением < ± 2°; относительная влажность 65 ± 15%; отсутствие магнитных и электрических полей; частота питающей сети 50 ± 1 Гц и т.д.

Дополнительная погрешность возникает при отклонении условий ис­пытания и эксплуатации средства измерения от нормальных. Например, приведенная погрешность прибора при нормальных условиях, т.е. в диапазоне температур (+20 ± 2)°С, не превышает 1%. Если температура лежит вне указанного диапазона, то погрешность может быть больше указанной.

Класс точности - это обобщен­ная метрологическая характеристика, определяемая пределами допус­каемых основной и дополнительных погрешностей, значения которых устанавливаются в стандартах на отдельные виды средств измерения. Класс точности стрелочных и самопишущих приборов обозначается одним числом с, равным максимально допускаемому зна­чению приведенной погрешности

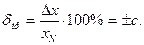(3.15)

Класс точности цифровых приборов указывается в виде дроби c/d , по которой определяется относительная погрешность

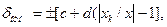(3.16)

где х_к – верхний предел измерения.

Значения c,d выбирают из следующего ряда:

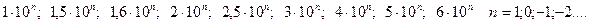
Порог чувствительности - это изменение измеряемой величины, вы­зывающее наименьшее изменение показаний, различимое при нормаль­ном для данного прибора способе отсчета.

Собственное потребление мощности прибором из цепи, в которой производится измерение, является важной характеристикой прибора. Особенно сильно это прояв­ляется при измерениях в маломощных цепях.

Описанные выше характеристики яв­ляются статическими, т.е. не зависящими от времени. Они имеют смысл только в том случае, если параметры измерительного прибора и значение измеряемой ве­личины остаются постоянными, а время измерения не ограничено.

Однако измеряемая вели­чина меняется по времени, измерение проводится за короткое время, параметры измерительного прибора изменяются и т.д.. Одновременный учет всех этих особенностей процесса измерения затруднителен. Поэтому предполагается, что средство измерения является линейной системой, т.е. может быть характеризовано линейным дифференциальным урав­нением с постоянными коэффициентами:

a₀d ⁿy/dt ⁿ + a₁d ^n-1y/dt ^n-1 +…+a_ny = x(t),

где а₀, a₁,.. ., а_n — постоянные коэффициенты.

При нулевых начальных условиях уравнение в опера­торной форме имеет вид

(а₀рⁿ + a₁p ^n-1 + …+ a_n)y(p) = x(p),

где p = d/dt – оператор дифференцирования.

Передаточной функцией СИ называется отношение изо­бражений по Лапласу выходной величины к входной:

W(р) = у(р)/х(р). (3.17)

Зная передаточную функцию преобразователя, можно определить его реакцию y(t) на заданное изменение измеряемой величины x(t) и опре­делить динамическую погрешность

Δу(t) = y{t) – у_ст, (3.18)

где y(t) - значение выходной величины СИ в момент времени t; у_ст - значение выходной величины, заданное его статической функцией преобразования.

При анализе динамических характеристик используются типовые входные воздействия: единичная и гармоническая функции.

Если в (3.17) подставить вместо р = jω, то можно определить частотную передаточную функцию СИ

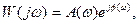(3.19)

где А(ω) - модуль частотной передаточной функции; φ(ω) - сдвиг фаз между входной и выходной величинами.

Зависимость модуля частотной передаточной функции от частоты А(ω) определяет амплитудно-частотную характеристику (АЧХ); зависимость ее аргумента от частоты φ(ω) определяет фазочастотную характеристику (ФЧХ).

К важным динамическим характеристикам приборов относится время установления показаний - промежуток времени, прошедший с момента подключения или изменения измеряемой величины до момента, когда отклонение указателя от установившегося значения не превышает 1,5% длины шкалы. Для цифровых приборов указывается время измерения, отсчитываемое от начала измерения до получения результата на отсчетном устройстве с нормированной погрешностью.

Надежность прибора - способность сохранять заданные характеристики при определенных условиях в течение заданного времени. Выход значения параметров и характеристик прибора за пределы нормы считается отказом. Отказ измерительного прибора может наступить, если его действительная погрешность станет больше ее нормирующего значения, определяемого классом точности.

Количественным показателем надежности является наработка на отказ - среднее время безотказной работы прибора. Наработка на отказ является статистической величиной. Она устанавливается для данной серии приборов на основании выборочных испытаний небольшой партии, входящих в эту серию.