Тема 11. Анализаторы спектра сигналов

Дата: 2025-05-01; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

11.1 Общие сведения о спектрах сигналов

Во многих практических случаях возникает потребность представления сигналов не только во временной, но и в частотной области и измерения на этой основе параметров этих сигналов.

В спектральной теории радиотехнических сигналов наибольшее распространение получили системы, в основу которых положен тригонометрический базис. В этом случае любая периодическая функция, для которой выполняется условие x(t) = x(t + nT), где Т – период, n – целое число; может быть представлена рядом Фурье одним из следующих видов:

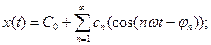(11.1)

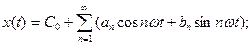(11.2)

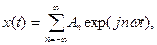(11.3)

где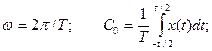

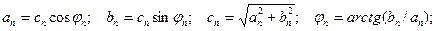
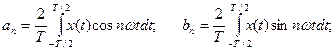
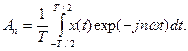
Совокупность коэффициентов С_n называется амплитудно-частотным спектром, а совокупность φ_n – фазо-частотным спектром.

Для спектрального анализа непериодических сигналов используется интеграл Фурье. Прямое преобразование Фурье позволяет переходить из временной области в частотную:

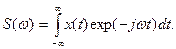(11.4)

Обратное преобразование Фурье наоборот обеспечивает переход из частотной области во временную:

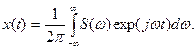(11.5)

11.2 Фильтровые анализаторы спектра

11.2.1 Анализатор спектра параллельного типа

Принцип действия анализатора спектра параллельного (одновременного) типа поясняется на (рис.11.1). В состав анализатора входят следующие элементы:

- аттенюатор, предназначенный для согласования входного сопротивления анализатора с выходным сопротивлением источника сигнала и изменением уровня входного сигнала;

- полосовые фильтры (ПФ) с полосой пропускания ∆f_ПФ, предназначенные для выделения участка спектра исследуемого сигнала;

- детекторы (Дет), предназначенные для получения огибающей сигнала на выходах соответствующих полосовых фильтров;

- индикатор.

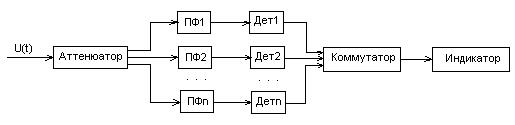
Рисунок 11.1 – Структурная схема анализатора спектра параллельного типа

Входной сигнал U(t), поступающий на вход анализатора после согласования по уровню, разделяется полосовыми фильтрами.

Напряжение с выхода каждого фильтра после детектирования подается через коммутатор на индикатор.

Количество фильтров n, необходимых для работы анализатора, равно

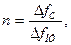(11.6)

где ∆f_C – полоса частот анализируемого сигнала.

Время анализа параллельного анализатора (Т_а) определяется временем установления напряжения на выходе фильтра и зависит от полосы пропускания ПФ: 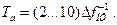(11.7)

Скорость параллельного анализатора зависит от числа фильтров:

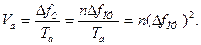
Такие анализаторы могут измерять спектры любых сигналов, за короткое время позволяют анализировать весь спектр сигнала, но из-за большого числа фильтров сложны при реализации и обладают большими габаритными размерами.

11.2.2 Анализаторы спектра последовательного типа

Принцип действия анализатора спектра последовательного типа состоит в выделении отдельных составляющих спектра сигнала с помощью одного полосового фильтра путем перестройки его резонансной частоты (рис.11.2).

Основными элементами анализатора спектра с перестраиваемым фильтром является аттенюатор, перестраиваемый полосовой фильтр, детектор, индикатор, генератор линейно изменяющегося напряжения (ГЛИН).

Закономерность изменения резонансной частоты полосового фильтра и напряжение развертки индикатора определяются одним устройством – ГЛИН, что обеспечивает своевременный вывод амплитуды соответствующей гармоники на горизонтальную линию индикатора.

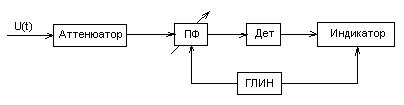
Рисунок 11.2 – Структурная схема анализатора с перестраиваемым фильтром

В таких анализаторах можно исследовать только сигналы, спектр которых за время анализа, т.е. за время перестройки фильтра в полосе обзора, не изменяется. Это периодически повторяющиеся сигналы.

Недостаток: перестройка резонансной частоты полосового фильтра приводит к изменению его добротности Q (добротности контура), что в свою очередь приводит к изменению амплитуды отклика и полосы пропускания.

11.3 Цифровые анализаторы спектра

В настоящее время применяются три разновидности цифровых анализаторов спектра, основой которых является преобразование сигнала в цифровой код и вычисление составляющих спектра с помощью цифровых вычислительных устройств.

11.3.1 Цифровой анализатор со сжатием сигнала во временной области

В таких анализаторах при небольшом времени анализа за счет искусственного расширения спектра исследуемого сигнала удается обеспечить высокую разрешающую способность. Расширение спектра при этом реализуется в цифровой форме.

Суть положительного эффекта такого анализатора заключается в том, что если искусственно в n раз расширить спектр сигнала (n∆F) и в n раз увеличить полосу пропускания (n∆f), то продолжительность анализа сократится в n раз при неизменной разрешающей способности:

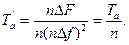(11.8)

Принцип действия блока сжатия информации (рис.11.3) строит­ся на предварительном преобразовании сигнала, поступающего на его вход. Из анализируемого сигнала берутся выборки мгновенных значе­ний с частотой, определяемой теоремой Котельникова. С помощью АЦП они преобразуются е цифровой код и последовательно записываются е запоминающее устройство (ЗУ).

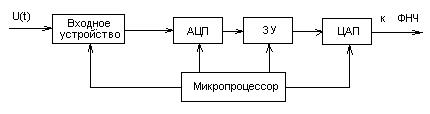
Рисунок 11.3 – Блок сжатия во временной области

Записанный в ЗУ блок информации считывается, но со скоростью, значительно большей скорости записи (10²...10⁴). Затем считанная ин­формация преобразуется в аналоговую форму. Таким образом, полученная сжатая во времени копия сигнала, может быть передана анализатору последовательного типа. Спектр сжатой копии и поло­са пропускания анализирующего фильтра расширяются. Однако время анализа уменьшается во столько раз, во сколько длительность сжатой копии меньше длительности сигнала, записанного в ЗУ.

Применение временного сжатия сигнала на низких частотах обес­печивает работу анализаторов последовательного типа в реальном вре­мени (анализатор СУ-73).

11.3.2 Анализаторы на цифровых фильтрах

Цифровые фильтры (ЦФ) выполняют операцию частотной филь­трации и позволяют получать при наличии управляющих воздействий различные АЧХ и ФЧХ, обеспечивая высокую стабильность параметров ЦФ и не нуждаются в подстройке.

Цифровые фильтры могут быть реализованы как аппаратными, так и программными средствами.

Процедура фильтрации в ЦФ представляет собой определенный ал­горитм обработки входного сигнала, в результате чего на выходе филь­тра появляются новые цифровые коды, соответствующие результатам фильтрации.

Передаточная функция ЦФ может быть представлена в виде дис­кретного преобразования Лапласа. Коэффициенты передаточной функ­ции определяют характеристики фильтра, для изменения которых до­статочно задать другие значения некоторым коэффициентам, т.е. зане­сти в ячейки памяти новые числа.

Таким образом, результат фильтрации определяется формой ана­лизируемого сигнала и параметрами АЧХ фильтра, зависящими от зна­чений коэффициентов реализуемой передаточной функции фильтра.

Упрощенная схема анализатора спектра на цифровых фильтрах представлена на (рис.11.4).

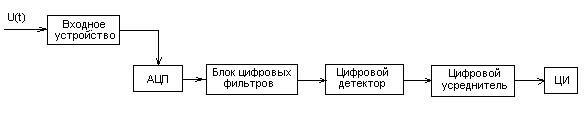
Рисунок 11.4 – Структурная схема анализатора спектра на цифровых фильтрах

Входной сигнал преобразуется в последова­тельность кодов, соответствующих числовым значениям сигнала в мо­менты выборки. Совокупность кодов с выхода цифровых фильтров по­ступает на цифровой детектор, где рассчитывается среднеквадратическое значение напряжения. После усреднения данных спектр сигнала отображается на экране анализатора в виде спектральных полос.

11.3.3 Анализаторы спектра на основе дискретного преобразования Фурье

Рассмотренное спектральное представление периодиче­ских и непериодических сигналов при определенных условиях распро­страняется и на дискретные сигналы, т.е. на сигналы, полученные из аналоговых путем взятия отсчетов в дискретные моменты времени.

Если периодический или непериодический сигнал x(t) преобразован
в дискретный сигнал S_i = x(i∆t), определенный на некотором интервале Т в моменты времени t₀,t₁,…t_i,…,t_N-1, разделенных интервалами ∆t = T/n, то такой дискретный сигнал может быть представлен дис­кретным преобразованием Фурье (ДПФ) в прямой и обратной форме:

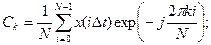(11.9)

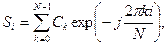(11.10)

где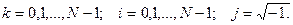

Выражения (11.9) и (11.10) устанавливают взаимнооднозначное соответствие между последовательностью отсчетов S_i и ее спектром C_k.

Особенностью ДПФ является свойство периодичности спектра С_k и временного ряда S_i, что обусловлено процедурой дискретизации. Это свойство создает определенные неудобства при практической реализа­ции ДПФ, что связано с наложением компонентов спектра от сосед­них периодов. Однако негативный эффект от этого влияния обычно может быть существенно снижен, например, за счет дополнительной фильтрации.

Непосредственное вычисление дискретного спектра по (11.9) явля­ется громоздкой вычислительной процедурой, требует выполнения боль­шого числа операций, что предъявляет высокие требования к быстро­действию вычислительных средств.

Требуется провести N² операций умножения и (N -1)N операций сложения с комплексными числами.

Указанные трудности существенно ослабляются при использовании алгоритмов быстрого преобразования Фурье (БПФ). Один из таких алго­ритмов предусматривает выделение из исходного временного ряда двух промежуточных подпоследовательностей. Спектры этих подпоследовательностей определяются раздельно, а затем находится спектр всего сигнала. Для нахождения спектра каждой подпоследова­тельности требуются N²/2 умножений и N(N/2 - 1)/2 сложений. При­менение БПФ позволяет уменьшить число проводимых операций при­близительно в N/lgN раз.

Рассматриваемый цифровой анализатор содержит систему на основе сигнального микроконтроллера (СМК), который осуществляет вычисления по алгоритму БПФ (рис. 11.5).

Исследуемый сигнал может вводиться как в анало­говой (АЦП входит в состав СМК), так и в цифровой форме.

Совокупность кодов, соответствующих мгновенным значениям сиг­налов в моменты дискретизации, запоминаются в ОЗУ сигнального микроконтроллера. Управление режимами работы СМК осуществляется с внешнего устройства управления (УУ) – центральным процессором. Алгоритм БПФ реализуется по программе, как правило, записан­ной в ПЗУ. Результаты вычисления запоминаются в ЗУ. Данные из ЗУ далее поступают в ЦАП и канал вертикального отклонения ЭЛТ блока индикации (БИ).

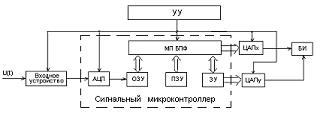
Рисунок 11.5 – Структурная схема анализатора спектра на основе БПФ

Сигналы, соответствующие частотам исследуемого сигнала, обес­печивают через ЦАП развертку на экране ЭЛТ. На экран цифрово­го дисплея одновременно с изображением спектра может выводиться алфавитно-цифровая информация о значениях различных параметров спектра исследуемого сигнала.