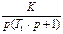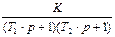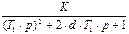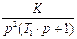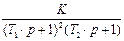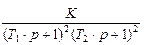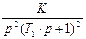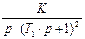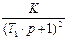Критерии устойчивости Михайлова
Для устойчивой системы необходимо и достаточно, чтобы годограф Михайлова при изменении частоты от нуля до бесконечности повернулся против часовой стрелки, начиная с вещественной оси, на число квадрантов равное порядку характеристического уравнения, последовательно проходя эти квадранты. Последовательность определения устойчивости:
в характеристическом уравнении заменяя оператор р на jω получают комплексный полином, представляющий собой вектор на комплексной плоскости;
разделяются вещественная и мнимая части вектора;
строится декартовая система координат. Ось абсцисс – вещественная часть вектора. Ось ординат - мнимая часть вектора;
в векторе задаются значения w от нуля до бecконечности и вычисляются отдельно вещественная и мнимая части этого вектора;
полученные значения вещественной и мнимой частей откладывают в виде точек на декартовой системе координат, соединяют плавной кривой и получают годограф вектора на комплексной плоскости или годограф Михайлова;
по виду прохождения годографа Михайлова судят об устойчивости данной системы.
Для устойчивости САУ годограф должен последовательно пройти все квадраты и в "n" уйти в бесконечность, где n-порядок характеристического уравнения.
ПРИМЕР 3. Определить устойчивость САУ с помощью критерия Михайлова по характеристическому уравнению примера 1.
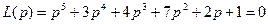
Решение. 1. Получают вектор на комплексной плоскости:
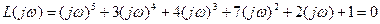
2. Выделяют вещественную и мнимую части:
.
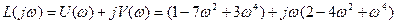3. Задаваясь значением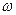 
(0; 0,2; 0,4; и т.д.), вычисляют отдельно вещественную часть (U( 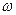)) и мнимую (jV( 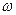))часть вектора на комплексной плоскости.
Все результаты вычисления показаны в таблице 2 и рис. 1.
Таблица 2
Значения U( 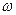) и jV( 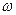) при изменении 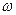от 0 до 10
| N точки | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|
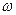
| 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 | 1.2 | 1.2 | 1.6 | 1.8 | 1.85 |
| U( )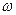
| 1 | 0.72 | -0.04 | -1.13 | -2.25 | -3.00 | -2.85 | -1.19 | 2.7 | 9.8 | 12.1 |
| V( )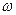
| 0 | 0.36 | 0.55 | 0.41 | -0.12 | -1.00 | -2.02 | -2.79 | -2.69 | -0.83 | 0.04 |
Рис. 1. Годограф Михайлова к примеру 3
Ответ: годограф Михайлова системы пятого порядка при изменении частоты от нуля до бесконечности последовательно проходит против часовой стрелки по всем квадрантам, начиная с вещественной оси, и в пятом квадранте при >1.85 уходит в бесконечность. Значит, данная САУ устойчива.
Годограф Михайлова проще построить по особым точкам. Особые точки - это пересечение годографа с осями координат. При пересечении с осью абсцисс мнимая часть характеристического вектора равна нулю. При пересечении с осью ординат вещественная часть вектора равна нулю. Определив эти точки пересечения, более просто строится годограф Михайлова. Причем, количество этих точек равно порядку характеристического уравнения. Так для системы пятого порядка определяется пять точек.
ПРИМЕР 4. Построить годограф Михайлова по особым точкам для вектора на комплексной плоскости примера 3.
Решение. 1. Определяют значение частот, при которых вещественная часть вектора на комплексной плоскости равна нулю.
U( ) 
;
; 
;
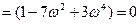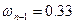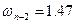Примечание: для построения годографа Михайлова берут только положительное значение .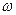
2. Вычисляют значение мнимой части вектора на комплексной плоскости при этих частотах.
3. Определяют значение частот, при которых мнимая часть вектора на комплексной плоскости равна 0 .
;
.
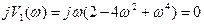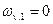
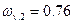
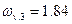4. Вычисляют значения вещественной части вектора на комплексной плоскости при этих частотах.
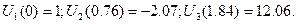
5. Результаты вещественной и мнимой частей характеристического уравнения для особых точек показаны в таблице 3.
Таблица 3
Результаты вычисления U( 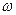) и V( 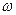) для особых точек
| № точки | 1 | 2 | 3 | 4 | 5 |
|
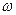
| 0 | 0,39 | 0,76 | 1,47 | 1,84 |
| U( )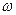
| 1 | 0 | -0,7 | 0 | 12.06 |
| V( )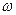
| 0 | 0.55 | 0 | -2.9 | 0 |
По результатам вычисления строят годограф Михайлова.
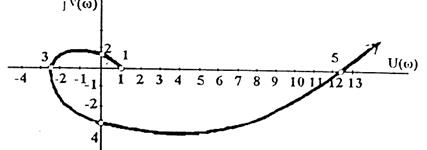
Рис. 2. Годограф Михайлова к примеру 4, построенный по особым точкам
Ответ: годограф Михайлова, построенный по особым точкам, полностью совпадает с годографом, построенным в примере 3. Система устойчивая.
Если определены частоты, при которых вещественная и мнимая части характеристического уравнения равны нулю, то нет необходимости строить годограф Михайлова для определения устойчивости данной системы. Можно использовать следствие из критерия Михайлова.
Для устойчивой системы необходимо и достаточно, чтобы корни уравнения вещественной и мнимой части характеристического уравнения с увеличением 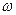сочередовались.
Согласно этому следствию нет необходимости вычислять значение мнимой и вещественной частей характеристического уравнения при особых точках. Достаточно проанализировать полученные частоты, при которых вещественная или мнимая части уравнения равны нулю.
Примечание: если при определении частот, при которых вещественная или мнимая части характеристического уравнения равны нулю, получают комплексное число, то это значит, что система неустойчива.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Записать заданное характеристическое уравнение согласно номеру варианта табл. 4.
2. Записать определитель Гурвица в числовом виде.
3. Выписать миноры Гурвица и определить их значения и сделать вывод об устойчивости САУ.
4. Определить значение всех коэффициентов таблицы Рауса.
5. Сравнить полученное значение коэффициентов первого столбца таблицы Рауса с отношением между минорами определителя Гурвица.
6. Получить из заданного характеристического уравнения выражение для вектора на комплексной плоскости.
7. Выделить мнимую и вещественную части для вектора на комплексной плоскости.
8. Построить годограф Михайлова.
9. Определить корни мнимой и вещественной частей выражения для вектора на комплексной плоскости.
Таблица 4
Варианты заданий
| Вариант | Параметры | |||||
| Wo ( p ) | T | K | T1 | T2 | d | |
| 1 |
| 0.2 | 1.5 | 2.0 | - | - |
| 2 | 0.4 | 3.0 | 1.6 | - | - | |
| 3 |
| 0.2 | 2.0 | 2.0 | 1.4 | - |
| 4 | 0.1 | 1.2 | 0.8 | 2.5 | - | |
| 5 | 0.4 | 1.0 | 2.5 | 4.0 | - | |
| 6 |
| 0.1 | 1.4 | 2.2 | - | 0.8 |
| 7 | 0.2 | 1.6 | 3.0 | - | 0.7 | |
| 8 |
| 0.4 | 1,9 | 1,25 | - | - |
| 9 | 0,6 | 4.0 | 2,55 | - | - | |
| 10 |
| 0.2 | 2.0 | 2.0 | 1.4 | - |
| 11 | 0.1 | 1.2 | 0.8 | 2.5 | - | |
| 12 | 0.4 | 1.0 | 2.5 | 4.0 | - | |
| 13 |
| 0.2 | 2.0 | 2.0 | 1.4 | - |
| 14 | 0.1 | 1.2 | 0.8 | 2.5 | - | |
| 15 | 0.4 | 1.0 | 2.5 | 4.0 | - | |
| 16 |
| 0.2 | 1.5 | 2.0 | - | - |
| 17 | 0.4 | 3.0 | 1.6 | - | - | |
| 18 |
| 0.4 | 1,9 | 1,25 | - | - |
| 19 | 0,6 | 4.0 | 2,55 | - | - | |
| 20 | 0.2 | 2.0 | 2.0 | - | - | |
| 21 |
| 0,6 | 4.0 | 2,55 | - | - |
| 22 | 0.2 | 2.0 | 2.0 | - | - | |
СОДЕРЖАНИЕ ОТЧЕТА
1. Заданное характеристическое уравнение.
2. Определитель Гурвица в числовом виде для данного варианта задания. Выделить миноры Гурвица и вычислить их значения.
3. Таблица Рауса в числовом виде.
4. Последовательность вычисления коэффициентов таблицы Рауса. (Коэффициенты можно вычислять отдельно и результаты вычисления записывать в таблицу Рауса).
5. Проверка правильности определения коэффициентов первого столбца таблицы Рауса через миноры Гурвица.
6. Выражение для вектора на комплексной плоскости с выделением мнимой и вещественной частей.
7. Годограф Михайлова (можно построить по особым точкам).
8. Определение корней мнимой и вещественной частей выражения для вектора на комплексной плоскости.
9. Определение устойчивости по следствию из критерия Михайлова.
ВОПРОСЫ для самопроверки
1. Что значит неустойчивая САУ?
Введение Необходимым условием работоспособности системы автоматического управления (САУ), является её устойчивость. Под устойчивостью принято понимать свойство системы восстанавливать состояние равновесия, из которого она была выведена под влиянием возмущающих факторов после прекращения их воздействия. система не может восстановить равновесное состояние, значение управляемой переменной (выходной величины) все больше отклоняется от заданного; такой процесс называется расходящимся, а система - неустойчивой
2. Как определяется устойчивость САУ по Ляпунову?
Согласно теории устойчивости Ляпунова, если все корни характеристического уравнения отрицательны, то система устойчива. Если хотя бы один корень положителен, то система не устойчива
3. Что значит критерий устойчивости?
Прямой метод анализа устойчивости систем, основанный на вычислении корней характеристического уравнения, связан с необходимостью определения корней. Вычисление корней для характеристических уравнений 1-й и 2-й степени достаточно просто. Существуют общие выражения для корней уравнений 3-й и 4-й степени, но эти выражения громоздки и практически малопригодны. Для уравнений более высоких степеней вообще невозможно написать выражения для определения корней. Поэтому важное значение для определения устойчивости системы приобретают правила, которые позволяют определить устойчивость системы без определения корней. Эти правила называют критериями устойчивости. С помощью критериев устойчивости можно не только установить, устойчива или нет система, но и выяснить, как влияют на устойчивость те или иные параметры и структурные изменения в системе. Различают две группы критериев устойчивости: алгебраические (Рауса и Гурвица), основанные на анализе коэффициентов характеристического уравнения, и частотные (Михайлова, Найквиста), основанные на анализе частотных характеристик.
Частотные критерии позволяют оценивать устойчивость системы, даже если имеются в наличии экспериментальные частотные характеристики, а уравнение динамики неизвестно.
4. Критерий устойчивости Рауса.
Критерий Рауса представляет собой систему неравенств, составленных по особым правилам из коэффициентов характеристического уравнения замкнутой системы.
Критерий Рауса удобен, когда заданы численные значения коэффициентов характеристического уравнения. Так как форма алгоритма, с помощью которого составляют таблицу Рауса очень удобна для программирования, то критерий Рауса широко применяют при исследовании с помощью ЭВМ, влияния на устойчивость либо коэффициентов характеристического уравнения, либо отдельных параметров системы.
5. Критерий устойчивости Гурвица.
6. Как выделяются миноры Гурвица?
7. Критерий устойчивости Михайлова.
8. Как может проходить годограф Михайлова для неустойчивых САУ?
9. Следствие из критерия устойчивости Михайлова.
СПИСОК ЛИТЕРАТУРЫ
Основная литература:
1. Рыбак Л.А. Теория автоматического управления. Часть I. Непрерывные системы [Электронный ресурс]: учебное пособие/ Рыбак Л.А.— Электрон. текстовые данные.— Белгород: Белгородский государственный технологический университет им. В.Г. Шухова, ЭБС АСВ, 2012.— 121 c.— Режим доступа: http://www.iprbookshop.ru/28400.— ЭБС «IPRbooks».
2. Рыбак Л.А. Теория автоматического управления. Часть II. Дискретные системы [Электронный ресурс]: учебное пособие/ Рыбак Л.А.— Электрон. текстовые данные.— Белгород: Белгородский государственный технологический университет им. В.Г. Шухова, ЭБС АСВ, 2012.— 65 c.— Режим доступа: http://www.iprbookshop.ru/28401.— ЭБС «IPRbooks».
Дополнительная литература:
3. Рубцов В.И. Методические указания к лабораторным работам по курсу «Теория автоматического управления» (линейные системы) [Электронный ресурс]/ Рубцов В.И.— Электрон. текстовые данные. — М.: Московский государственный технический университет имени Н.Э. Баумана, 2010. — 40 c.— Режим доступа: http://www.iprbookshop.ru/31571. — ЭБС «IPRbooks»
Интернет-ресурсы:
1. Электронный ресурс http://window.edu.ru/catalog/
2. Электронный ресурс http://www.studmed.ru/
1.Гузенко А.И. Основы теории автоматического регулирования / под ред. В.В. Солодовникова. - М.: Высшая шк., 1977.
2.Анхимюк В.Л. Теория автоматического управления.-3-е изд. / В.Л.Ахимюк. - Минск: Высшая шк., 1979.
3.Иващенко Н.Н. Автоматическое регулирование / Н.Н.Иващенко. - М.: Машиностроение. 1972.