Кафедра интеллектуальных систем в управлении и автоматизации
Федеральное агентство связи
Ордена Трудового Красного Знамени
федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра интеллектуальных систем в управлении и автоматизации
В. А. ВЕРБА
ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
« ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ»
Методические указания к выполнению практической работы
для студентов-бакалавров
по направлениям подготовки:
15.03.04 «Автоматизация технологических процессов и производств»,
27.04.04 «Управление в технических системах»
Москва 2019 г.
ВВЕДЕНИЕ
Одна из основных задач теории автоматического управления - это определение устойчивости системы. Только устойчивая САУ может выполнять возложенные на нее задачи.
Под устойчивостью понимают способность системы самостоятельно возвращаться в состояние равновесия после вывода ее из этого состояния и снятия всех возмущающих воздействий.
В зависимости от характера переходного процесса линейной системы различают три основных случая поведения системы после возмущающего воздействия:
1) система не может восстановить равновесное состояние, значение управляемой переменной (выходной величины) все больше отклоняется от заданного; такой процесс называется расходящимся, а система - неустойчивой;
2) система возвращается в равновесное состояние, значение управляемой переменной отличается от заданного на величину статической ошибки, такой процесс называется сходящимся, а система - устойчивой;
3) система характеризуется установившимся периодическим движением, такой процесс называется колебательным, а система будет находиться на границе асимптотической устойчивости.
Если система описывается линейными дифференциальными уравнениями, то ее устойчивость не зависит от величины и вида возмущения, а зависит только от знака вещественной части корней характеристического уравнения.
Согласно теории устойчивости Ляпунова, если все корни характеристического уравнения отрицательны, то система устойчива. Если хотя бы один корень положителен, то система не устойчива.
Определение знаков корней характеристического уравнения 4-го и более высокого порядка путем его решения затруднительно, поэтому применяются косвенные методы анализа, или критерии устойчивости, которые позволяют определить знаки корней характеристического уравнения без решения этого уравнения.
Цель работы: научиться определять устойчивость по алгебраическим критериям Рауса, Гурвица, по частотному критерию Михайлова.
ОСНОВНЫЕ ПОЛОЖЕНИЯ
Устойчивость линейных систем не зависит от величины возмущения. Система устойчивая при малых возмущениях будет устойчивой и при больших возмущениях, поэтому достаточно исследовать и определить устойчивость в малом, т.е. найти устойчивость на основе анализа уравнения, записанного в форме приращений. Допустим, что в установившемся состоянии регулируемая величина имеет некоторое значение x0. Выведем систему из этого состояния при помощи какого-либо воздействия так, чтобы x0 изменилась на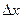 
. И после этого устраним причину, вызвавшую это изменение, тогда система будет устойчивой, если будет выполняться условие: 
.
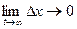В случае невыполнения этого условия система будет неустойчивой. Допустим, что изменение регулируемой величины в процессе регулирования описывается линейным уравнением n-го порядка с постоянными коэффициентами, тогда отклонение 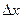также будет описываться дифференциальным уравнением этого порядка. Интегрируя полученное уравнение, находят закон изменения интересующей переменной по времени, согласно которому можно сделать заключение о характере переходного процесса (устойчивый, неустойчивый). Устойчивость системы определяют характером свободного движения системы, т.к. свободное движение системы описывается однородным дифференциальным уравнением (без правой части), то для нахождения условий устойчивости достаточно исследовать свойства решения однородного дифференциального уравнения. В общем случае для системы n-го порядка имеем дифференциальное уравнение, которое описывает поведение отклонения 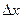регулируемой величины:
,
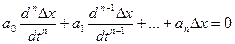где а0, а1, аn- постоянные коэффициенты, величина которых зависит от параметров САУ.
Решение может быть представлено в виде: =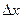 
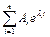, где Ai- постоянная интегрирования, определяется из начальных условий; 
- корни, характеризующие свободное движение и определяемые из характеристического уравнения: 
.
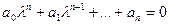Исследуем характеристическое уравнение с точки зрения устойчивости системы. Согласно определению для устойчивости системы необходимо, чтобы отклонение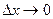 
при t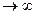 
, а это возможно только тогда, когда все составляющие уравнения с течением времени стремятся к 0. Поскольку все Ai=const, то, следовательно, характер поведения каждой составляющей 
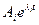зависит от . Если - положительное, вещественное число, то составляющая 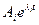будет увеличиваться до бесконечности. При отрицательных вещественных корнях составляющая свободного движения при t 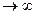монотонно убывает до 0.