Задание №3 – трёхмерная графика

//код 6
[X,Y]=meshgrid(0:.2:1,0:.02:1);//meshgrid создаёт матрицы или трёхмерные массивы
Z=X.^2+Y.^2;//функция
xtitle('$\huge z=x^2+y^2$');//добавление заголовка в графическое окно
mesh(X,Y,Z);//mesh создает график трехмерной сетки
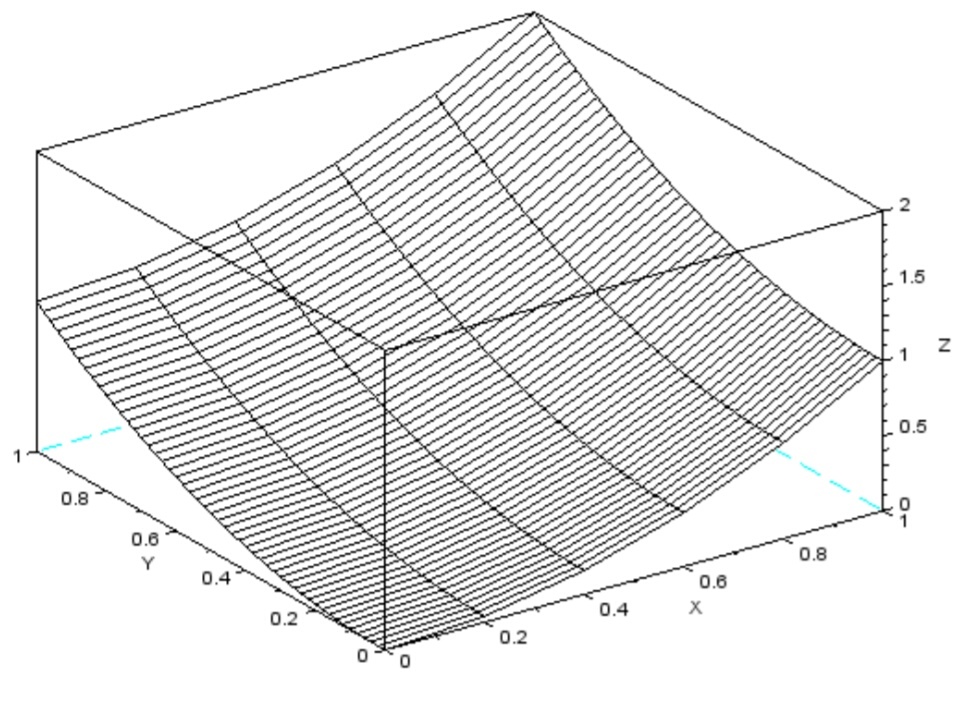
Рисунок 18 трехмерная сетка

Примечание: используйте функцию meshgrid() и mesh().
//код 7
[x,y]=meshgrid(-2:0.24:2,-2:0.24:2);//область определения х, у с шагами 0.24(т.к вариант- 24)
--> x0=0;
--> y0=0;
--> z=exp(-((x-x0).^2/2+(y-y0).^2/2));//функция
--> xtitle('$\huge z(x,y)=exp(-((x-x0).^2/2+(y-y0).^2/2))$');\
mesh(x,y,z);//реализация графика
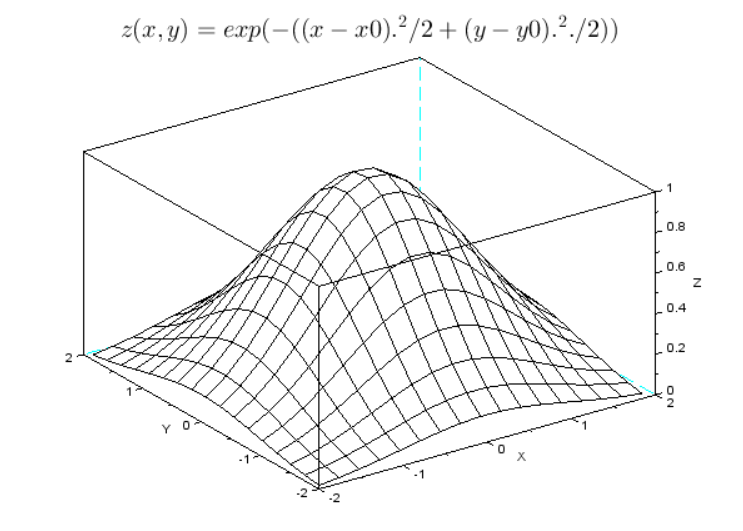
Рисунок 19 сетчатый график функции

//код 8
[x,y]=meshgrid(-1:0.1:1,-1:0.1:1);//создание векторов
--> N=24;//номер варианта
--> z=N/2.*sin(x.*2*%pi).*cos(1.5*%pi*y).*(1-x^2)*y.*x.*(1-y);//функция
--> mesh(x,y,z);//реализация графика
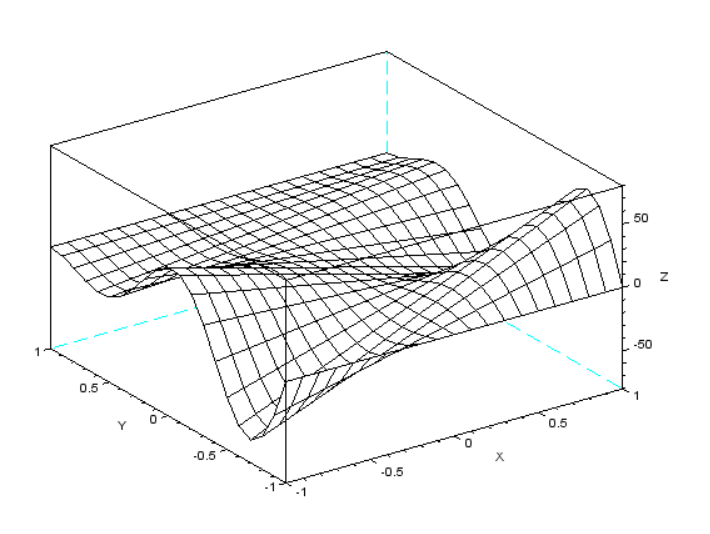
Рисунок 20 прозрачная сетчатая поверхность функции z(x,y)=N/2 sin(2πx) cos(1.5πy) (1-x^2 )yx(1-y)
//к коду 8 приписываем следующие строчки
mesh_handle=get("hdl")//функция get позволяет получить текущий графический объект и
возвращает различные свойства, т.к. mesh имеет flag_color=0(белый или без цвета)
mesh_handle.color_mode=2//даем код цвета (синий)
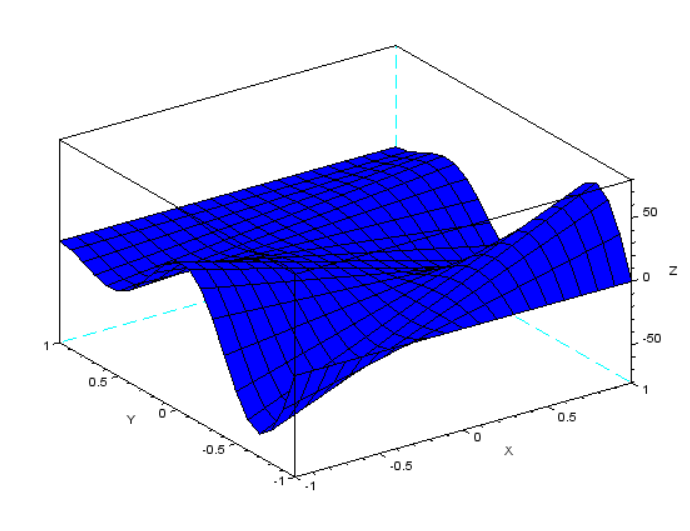
Рисунок 21 непрозрачная сетчатая поверхность функции z(x,y)=N/2 sin(2πx) cos(1.5πy) (1-x^2 )yx(1-y)
3.4. Постройте каркасную поверхность функции z (x y) с помощью команд
surf(X, Y, Z), surf(X, Y, Z, 'facecol','interp') и приведите их в отчете. Добавьте
также отображение сетки в трёхмерном пространстве.
//код 9
[x,y]=meshgrid(-1:0.1:1,-1:0.1:1);
N=24;//номер варанта
z=N/2.*sin(x.*2*%pi).*cos(1.5*%pi*y).*(1-x^2)*y.*x.*(1-y);//функция графика
surf(x,y,z);//строит 3d графики
xgrid(2);//сетка
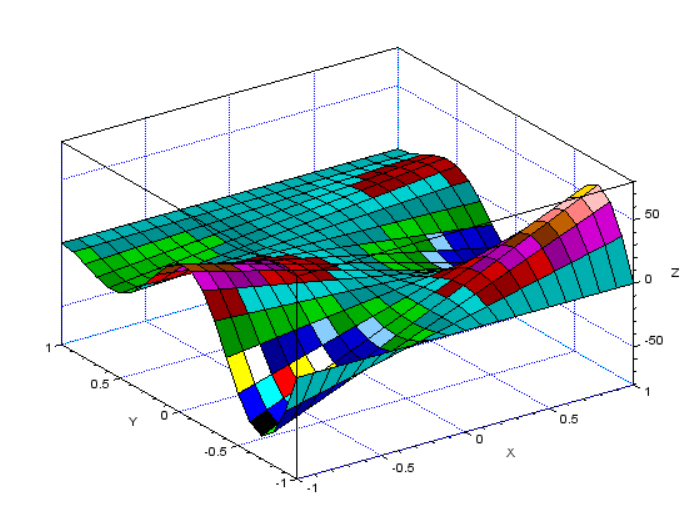
Рисунок 22 каркасная поверхность с помощью функции surf
//код 10
[x,y]=meshgrid(-1:0.1:1,-1:0.1:1);
N=24;//номер варанта
z=N/2.*sin(x.*2*%pi).*cos(1.5*%pi*y).*(1-x^2)*y.*x.*(1-y);//функция графика
surf(x,y,z,'facecol','interp');//интерполированный режим затенения flag_color=3
xgrid(2);//сетка

Рисунок 23 каркасная поверхность с помощью функции surf(x,y,z,'facecol','interp')
3.5. Постройте каркасную поверхность функции z= (x y с) помощью
следующего набора команд:
surf(X, Y, Z);
f = gcf();
f.color_map = hsvcolormap(32)
Результаты приведите в отчете и объясните что делает каждая строка.
--> surf(X, Y, Z) //строит каркасную поверхность
--> f = gcf(); //gcf-возвращяет дескриптор текущего графического окна
--> f.color_map = hsvcolormap(32)//изменяет насыщенность оттенка
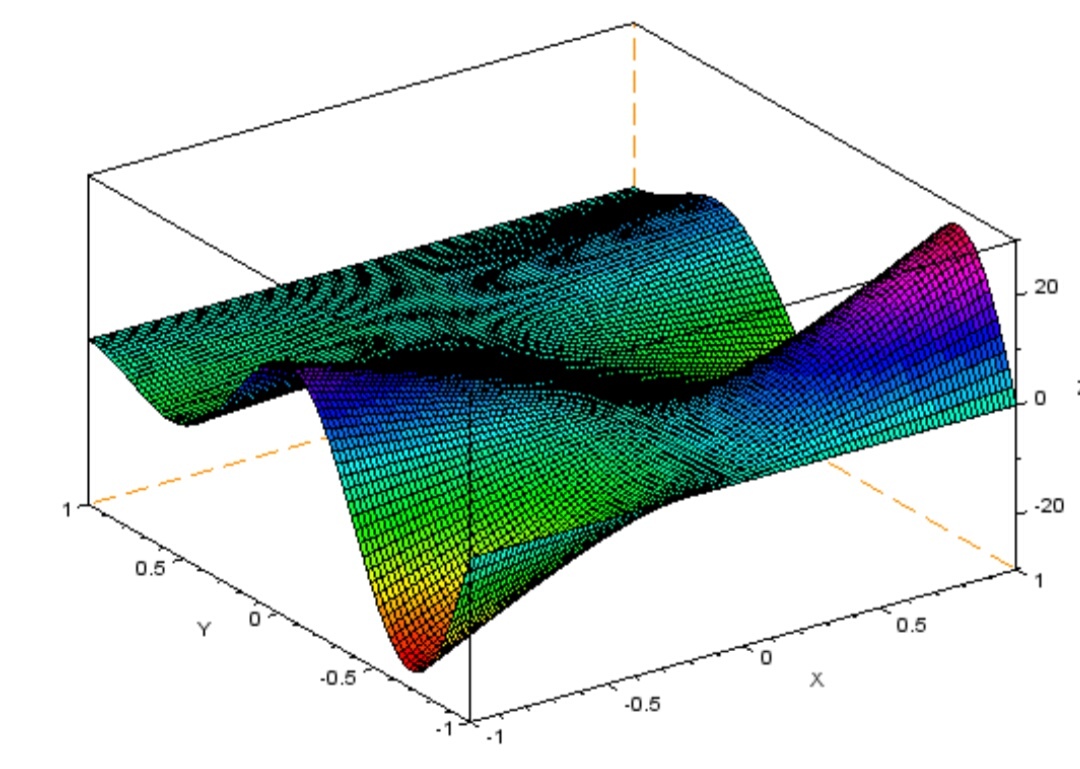
Рисунок 24 каркасная поверхность (изменение насыщенности)
3.6. Постройте каркасную поверхность функции z (x y) с помощью команд
аналогичным выше со следующими палитрами: autumncolormap,
coolcolormap, pinkcolormap. Посмотрите, как будет меняться палитра при
изменении параметра n (например при числах 8, 16, 32).
--> f = gcf(); //gcf-возвращяет дескриптор текущего графического окна
--> f.color_map = autumncolormap (32)//цветовая карта от красного до
оранжевого, до желтого цвета. При изменении параметра n в большую
сторону палитра становится более четким(начинает приближаться к желтому
цвету)
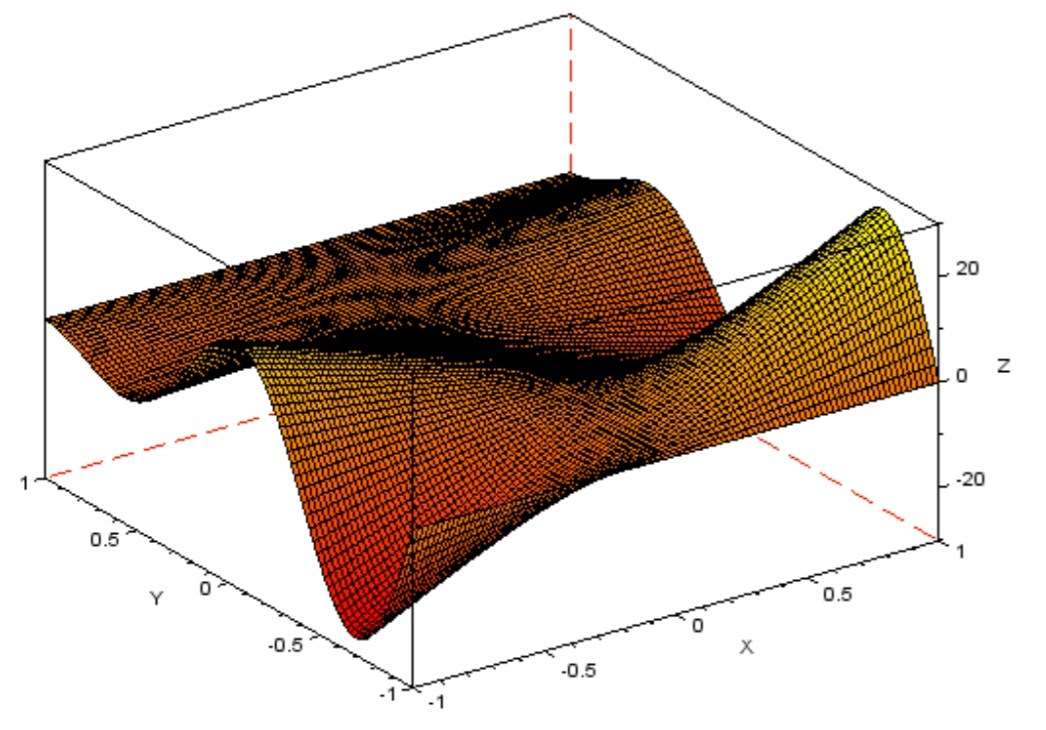
Рисунок 25 поверхность с палитрой f.color_map = autumncolormap (32)
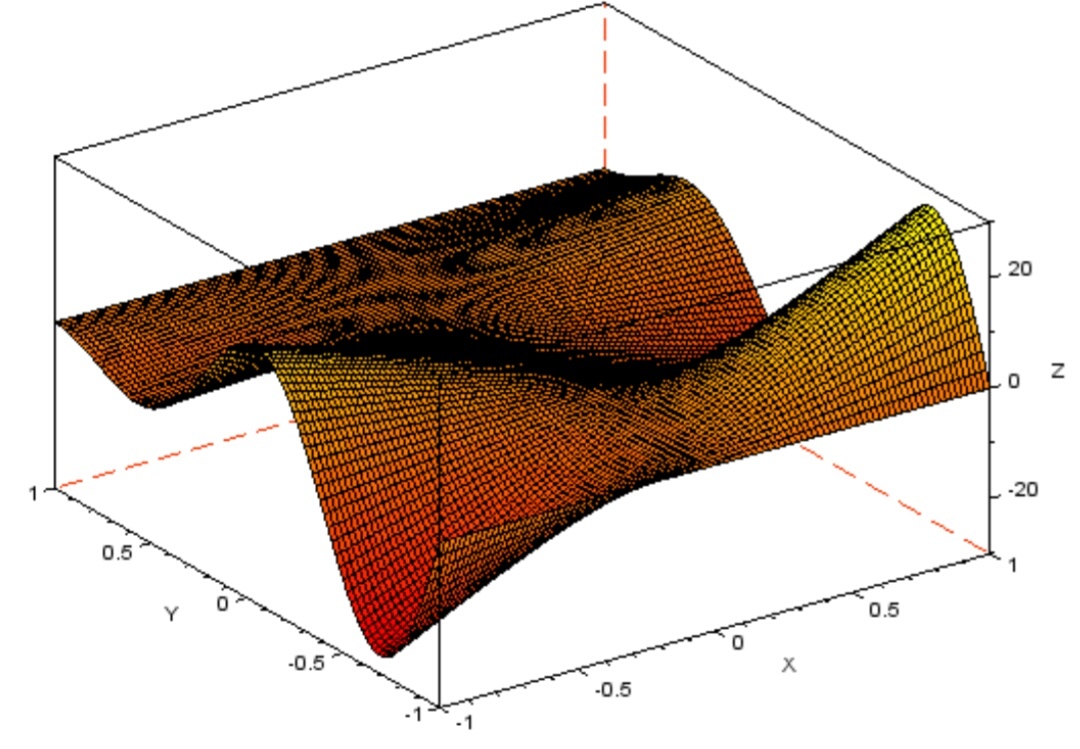
Рисунок 25 поверхность с палитрой f.color_map = autumncolormap (16)
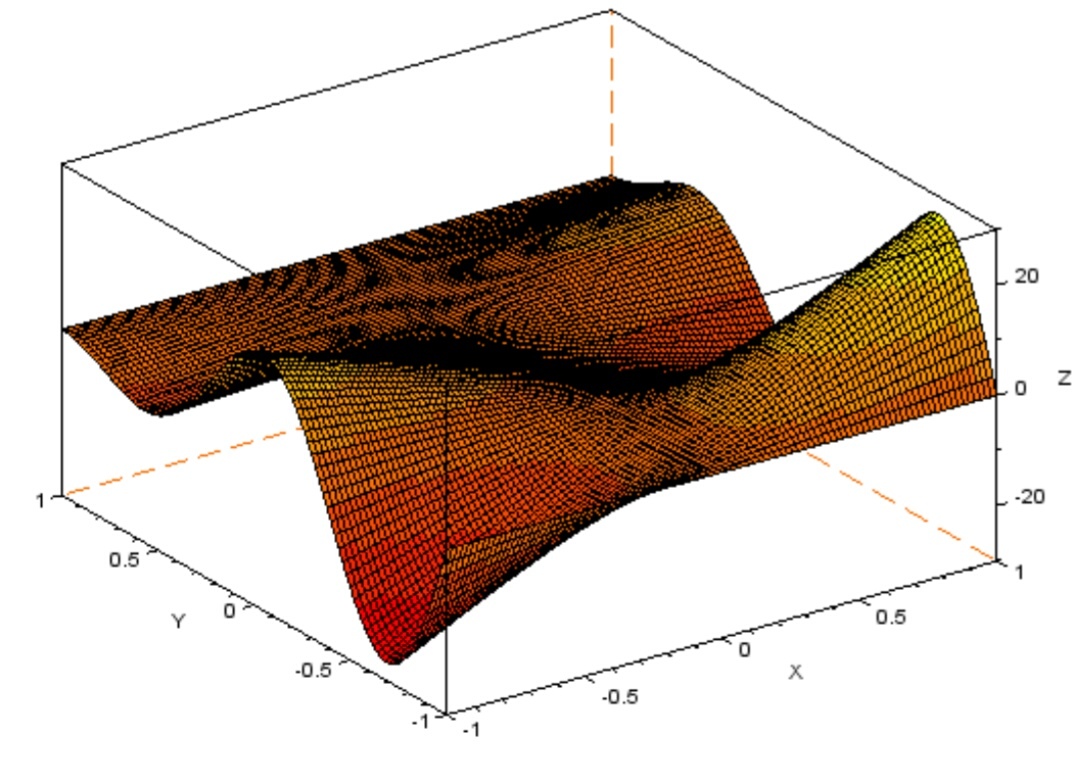
Рисунок 27 поверхность с палитрой f.color_map = autumncolormap (8)
--> f = gcf(); //gcf-возвращяет дескриптор текущего графического окна
--> f.color_map = coolcolormap (32)//coolcolormap- вычисляет цветовую карту
с n цветами, варьирующимися от голубого до пурпурного. При изменении
параметра n в большую сторону палитра меняется, цвета распределяются
иначе.
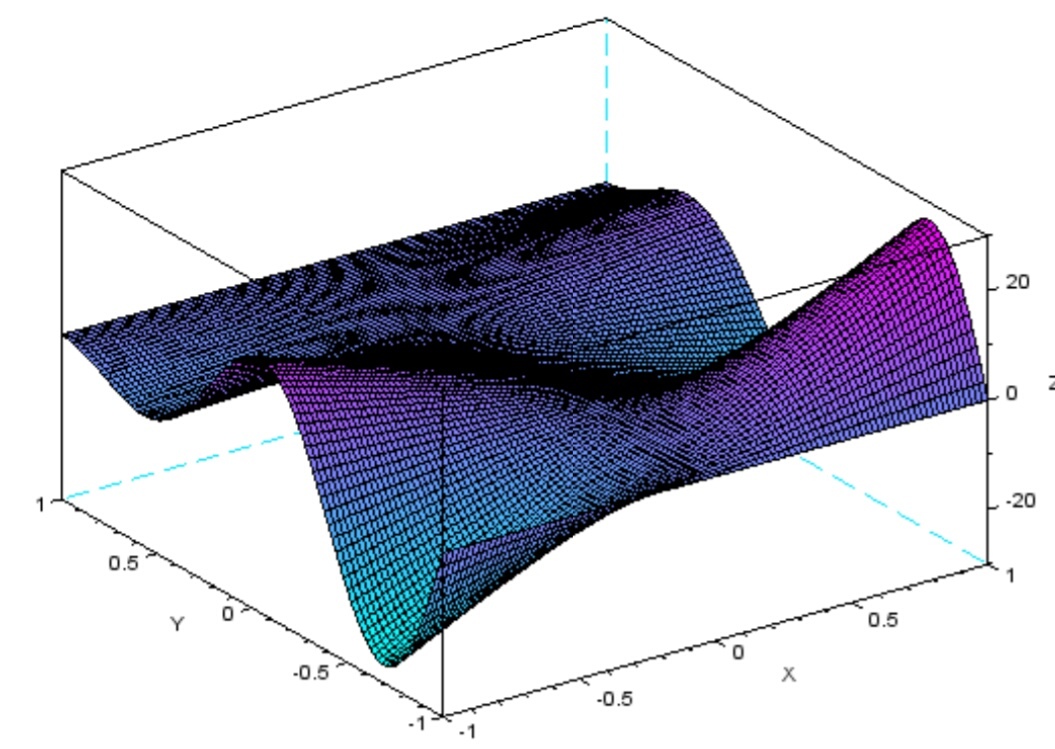
Рисунок 28 поверхность с палитрой f.color_map = coolcolormap (32)
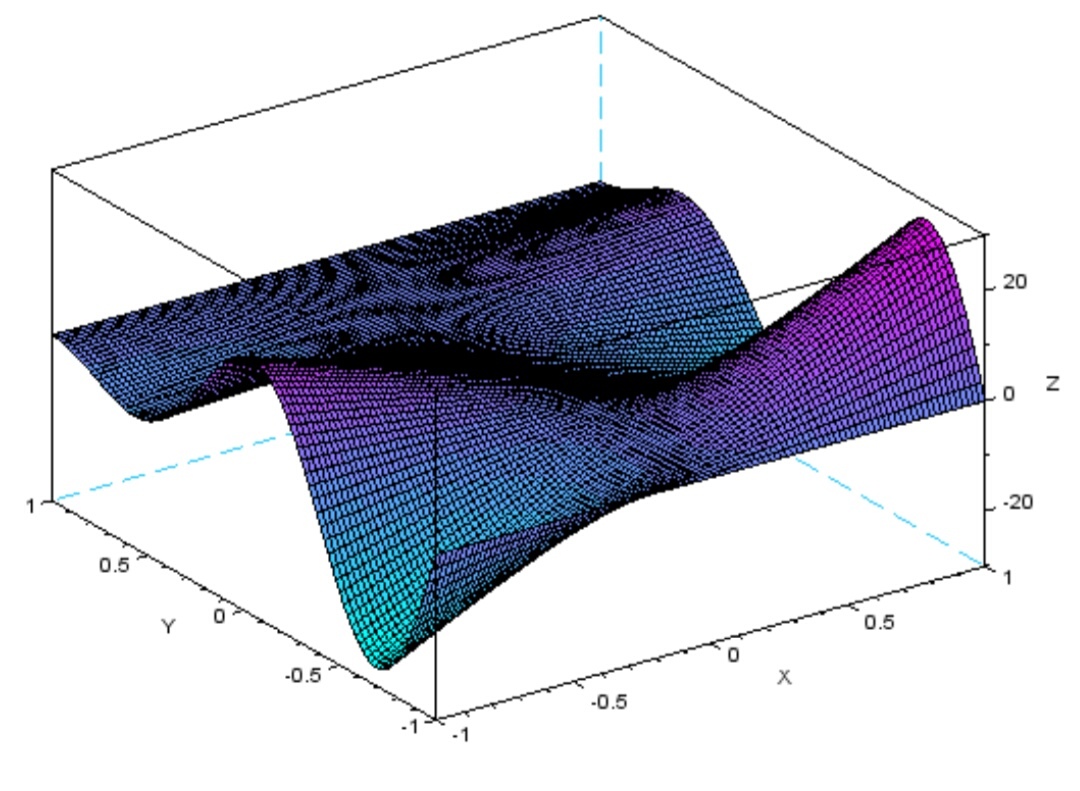
Рисунок 29 поверхность с палитрой f.color_map = coolcolormap (16)

Рисунок 30 поверхность с палитрой f.color_map = coolcolormap (8)
--> f = gcf(); //gcf-возвращяет дескриптор текущего графического окна
--> f.color_map = pinkcolormap (32)//pinkcolormap - раскрашивание цвета
сепии на черно-белые изображения. При изменении параметра n в большую
сторону палитра меняется, цвета начинают приближаться к белому
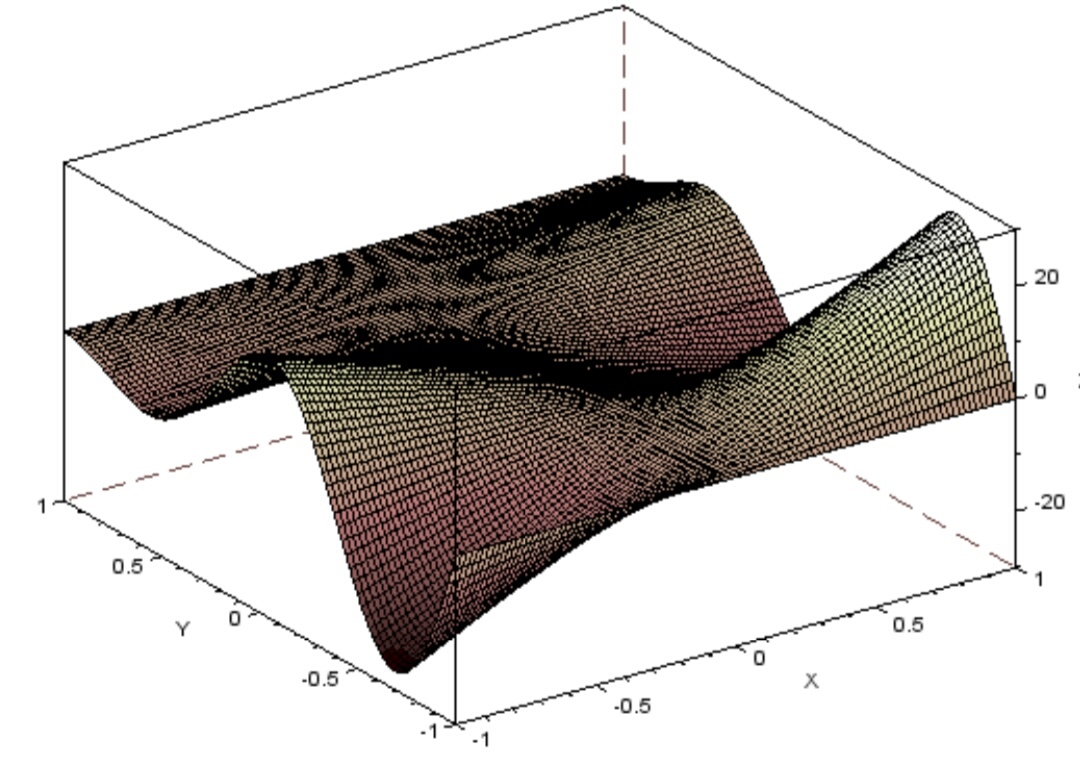
Рисунок 31 поверхность с палитрой f.color_map = pinkcolormap (32)
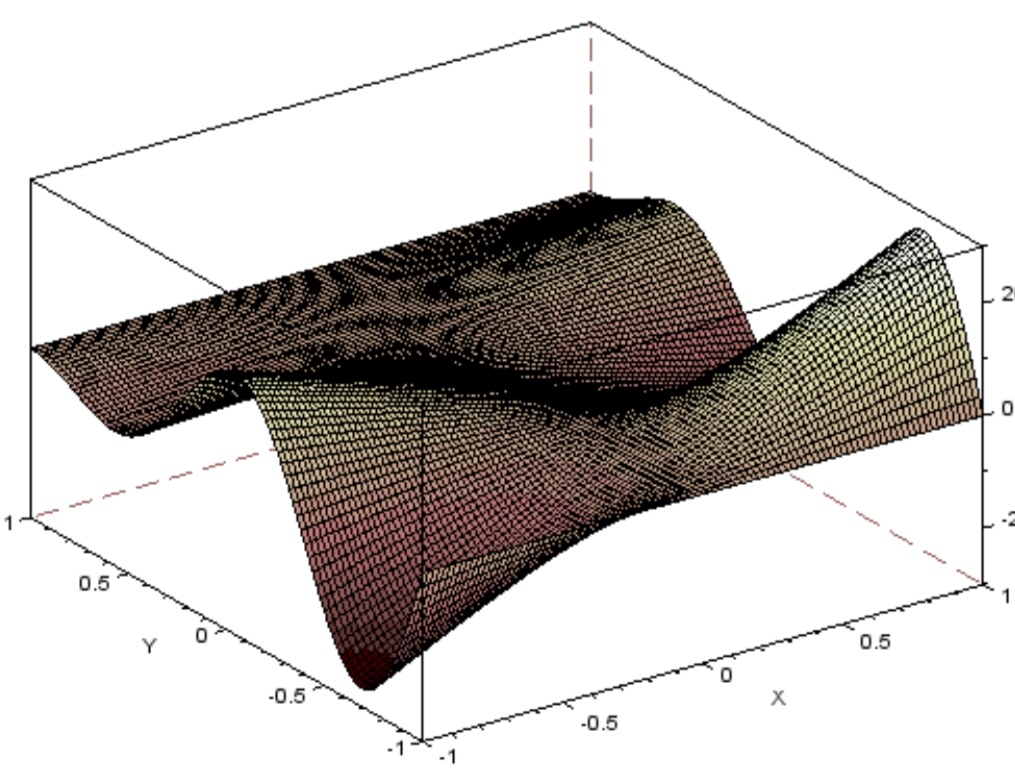
Рисунок 32 поверхность с палитрой f.color_map = pinkcolormap (16)

Рисунок 33 поверхность с палитрой f.color_map = pinkcolormap (8)
3.7. C помощью команды param3d(x,y,z) постройте параметрическую кривую
в объёмном пространстве, которая описывается следующим образом:
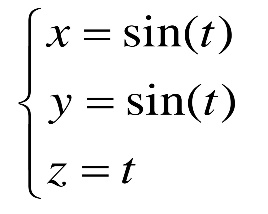
где параметр t - вектор, который должен изменяться от 0 до 10π. Шаг следует
выбирать в диапазоне от 0.001 до 0.01.
//код 11
t=[0:0.007:10*%pi];//вектор t в диапазоне [0,10π] и с шагом 0.007
--> clf
--> x=sin(t);//функция х
--> y=sin(t);//функция у
--> z=t;//функция z
--> param3d(x,y,z,theta=[2],alpha=[4]);//param3d-построение одной кривой в 3D декартовой рамке
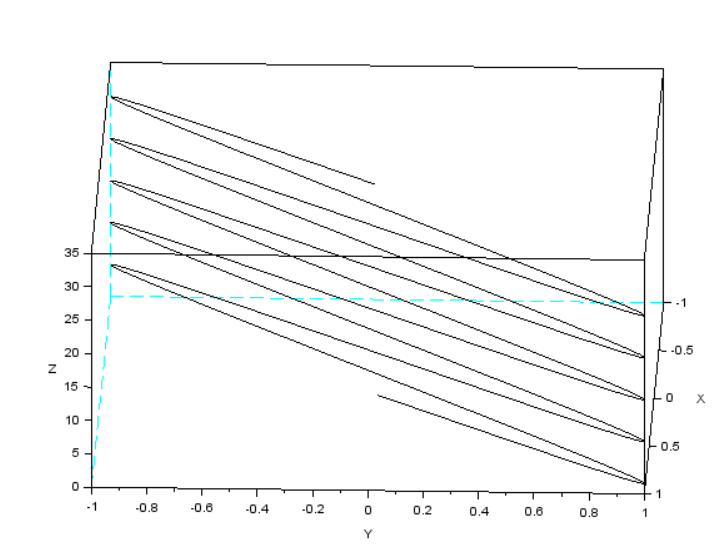
Рисунок 34 реализация param3d
Задание №4 М-файлы и функции
Работа с М-файлами и пользовательскими функциями.
4.1 Описать и реализовать следующий код, создать файл функцию
//код 12
x = [0:0.1:10];//создает вектор х в диапазоне [0,10] с шагом 0.1
--> f = exp(-x);//функция f
--> subplot(1, 2, 1)//subplot- устанавливает текущие оси для выбора ячейки текущей разграфлённой фигуры
plot(x, f)//строит график f
--> g = sin(x);//функция g
--> subplot(1, 2, 2) // subplot(m,n,p) виртуально разделяет графическое окно на матрицу
подокон размером m-на-n, и выбирает p-тое подокно для получения графика
--> plot(x, g)//строит график g
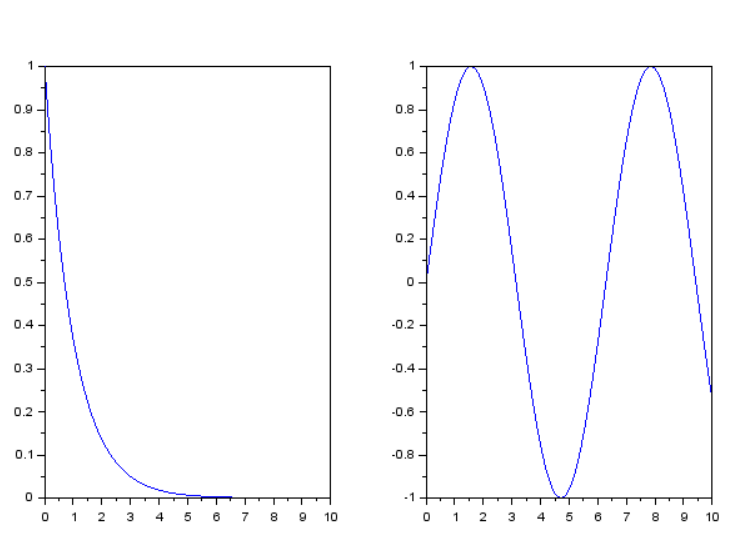
Рисунок 35 реализация функции subplot
//код 11 данная программа строит график двух функций и показывает их в
одном окне с разными осями
--> exec(“main.sce”)//как только набираем в консоли эту команду, сразу
появляется графическое окно. Мы создали отдельную файл-функцию main,
которая реализует код 11.
4.2. Постройте график файл-функции myfun с помощью команд plot и fplot2d.
В файле-функции myfun должно рассчитываться следующее выражение:
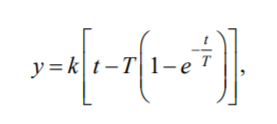
где
k =N , N - номер варианта по списку,
T =N/50
. В качестве входного
аргумента файл-функция должна принимать вектор
t
, который должен быть
задан на интервале [0, 5] с шагом 0.01. Таким образом, М-файл функции
должен иметь следующее заглавие:
function f = myfun(t)
В командной строке MATLAB вызов этой функции происходит
следующим образом:
--> y = myfun(t)
В результате чего создастся вектор-строка y с тем же числом элементов,
что и вектор
t . После этого можно воспользоваться функцией plot.
Чтобы воспользоваться функцией fplot2d необходимо выполнить
следующую команду:
--> fplot2d(t, myfun),
где t – вектор времени.
//код 12-файл_функция myfun
function y=myfun(t)
N=24//вариант
T=N/50;
k=N;
y=k.*(t-T.*(1-exp(-t./T)));
endfunction
Содержание консоли:
--> t=[0:0.01:5]
t =
……………………
--> exec("myfun.sce");
--> y=myfun(t)//создается вектор-строка у
--> plot(t,y)
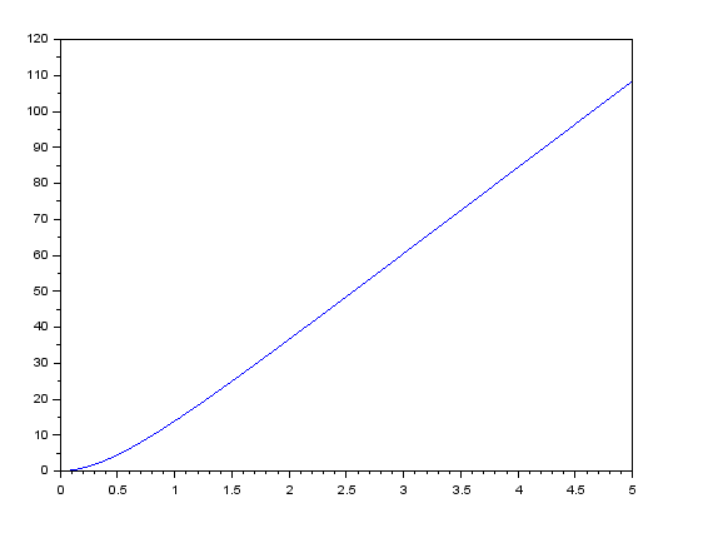
Рисунок 36 реализация графика plot через файл_ функцию “myfun.sce”
--> fplot2d(t,myfun)

Рисунок 37 реализация графика fplot2d(t,myfan) через файл_ функцию “myfun.sce”
4.3. Напишите файл-функцию root2, которая находит только действительные
корни квадратного уравнения, а при наличии комплексного корня выдает
сообщение об ошибке. В демонстрационных примерах второй коэффициент
квадратного уравнения должен быть равен вашему номеру по списку в
журнале группы.
//код 13
function [y1, y2]=root2//ax^2+bx+c=0
a=input("Введите а:")
c=input("Введите c:")
b=24//номер варианта
D=sqrt(b.^2-a.*c)//дискриминант квадратного уравнения
y1=(-2+D)./2*a//первый корень
y2=(-2-D)./2*a//второй корень
if D<0//функция если
then disp("Ошибка")//тогда
else disp(y1,"Значение у1:")//в противном случае, вывести на экран значения корней
disp(y2,"Значение y2:")
end
endfunction
Содержание консоли:
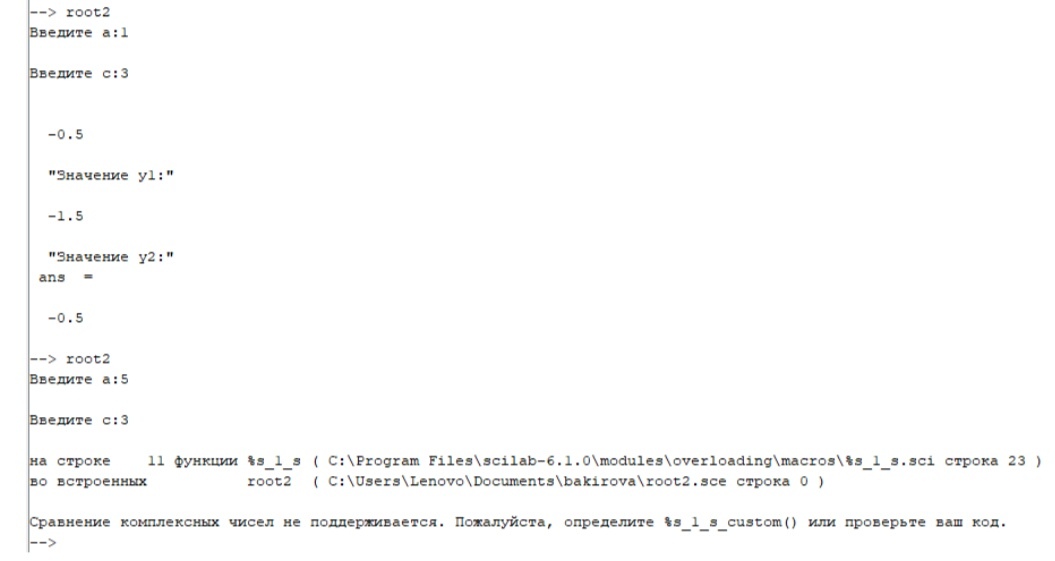
Рисунок 38 результат программы код 13

>> B = Bezie(P0,P1,P2,P3,step)
34
В отчёте приведите не менее 5 графиков кривых Безье для различных
комбинаций опорных точек P0,P1,P2,P3.
Решение
//код 14-файл Bezie
function B=Bezie(P0, P1, P2, P3, step)
t=[0:step:1];//вектор t с шагом step
X=((1-t).^3)*P0(1,1)+(3.*t.*(1-t).^2)*P2(1,1)+(3.*t.*t.*(1-t))*P3(1,1)+(t.*t.*t).*P1(1,1)//
координата по Х
Y=((1-t).^3)*P0(2,1)+(3.*t.*(1-t).^2)*P2(2,1)+(3.*t.*t.*(1-t))*P3(2,1)+(t.*t.*t).*P1(2,1)//
координата по У
B=[X;Y];//матрице B задаем координаты ХУ
plot(X,Y)//строит кривую безье
endfunction
//набираем в консоли
--> P0=[1;2]//вектор Р0
P0 =
1.
2.
--> P1=[2;4]//вектор Р1
P1 =
2.
4.
--> P2=[4;1]//вектор Р2
P2 =
4.
1.
--> P3=[2;2]//вектор Р3
P3 =
2.
2.
35
--> step=0.01//шаг вектора t
step =
0.01
--> B=Bezie(P0,P1,P2,P3,step)//вызываем файл_ функцию Bezie
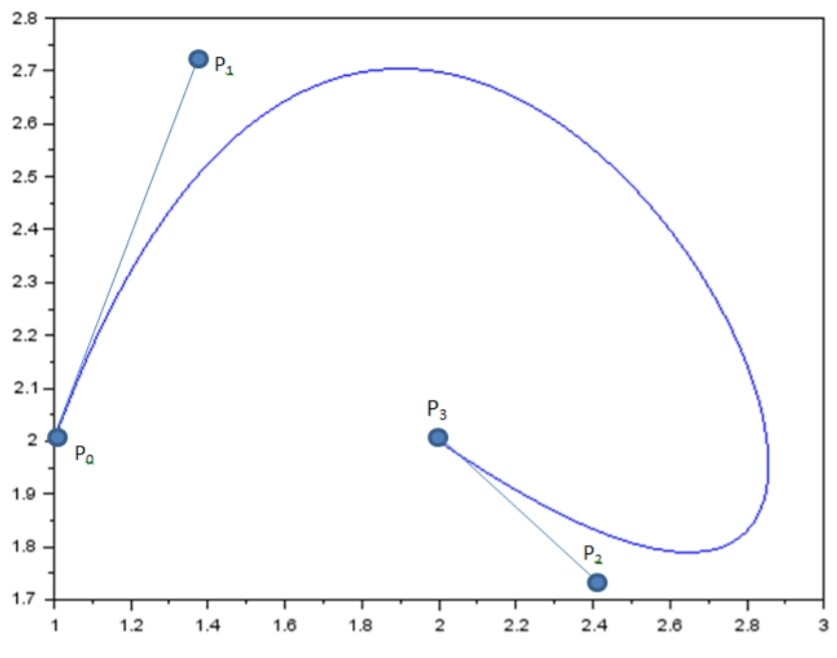
Рисунок 39 график кривой безье Р0,Р1,Р2,Р3
--> B=Bezie(P1,P0,P2,P3,step)//меняем порядок
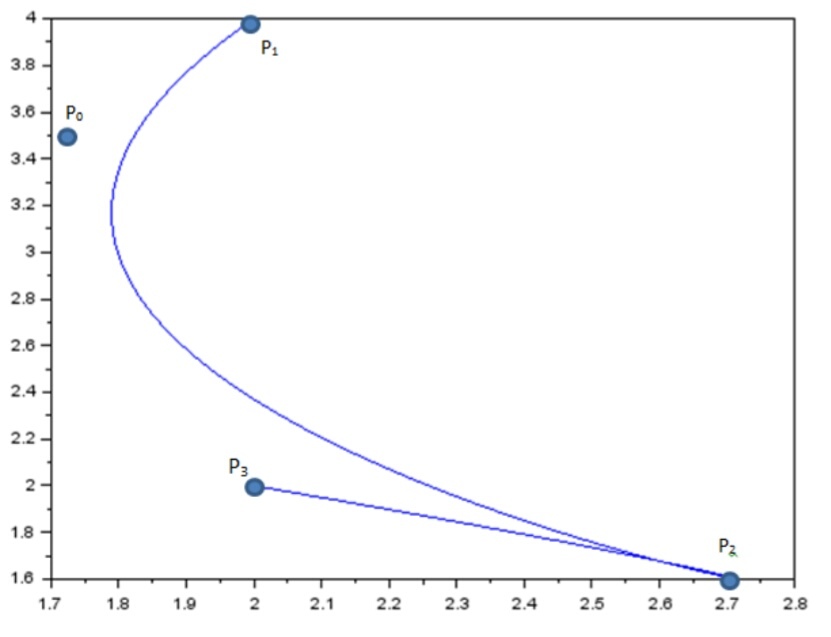
Рисунок 40 график кривой безье Р1,Р0,Р2,Р3
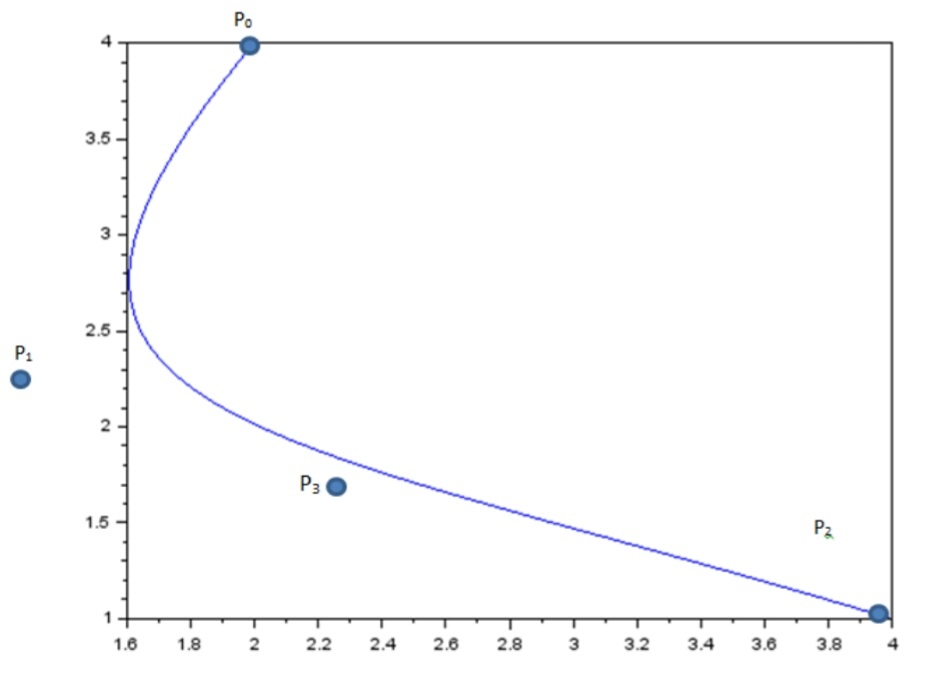
Рисунок 41 график кривой безье Р0,Р1,Р3,Р2
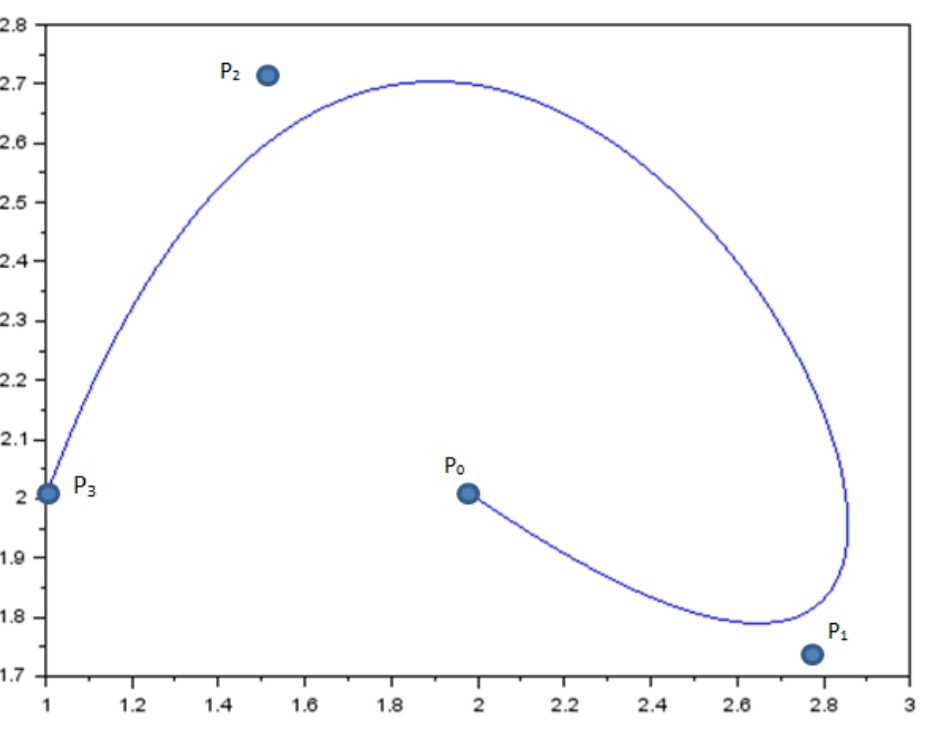
Рисунок 42 график кривой безье Р3,Р2,Р1,Р0
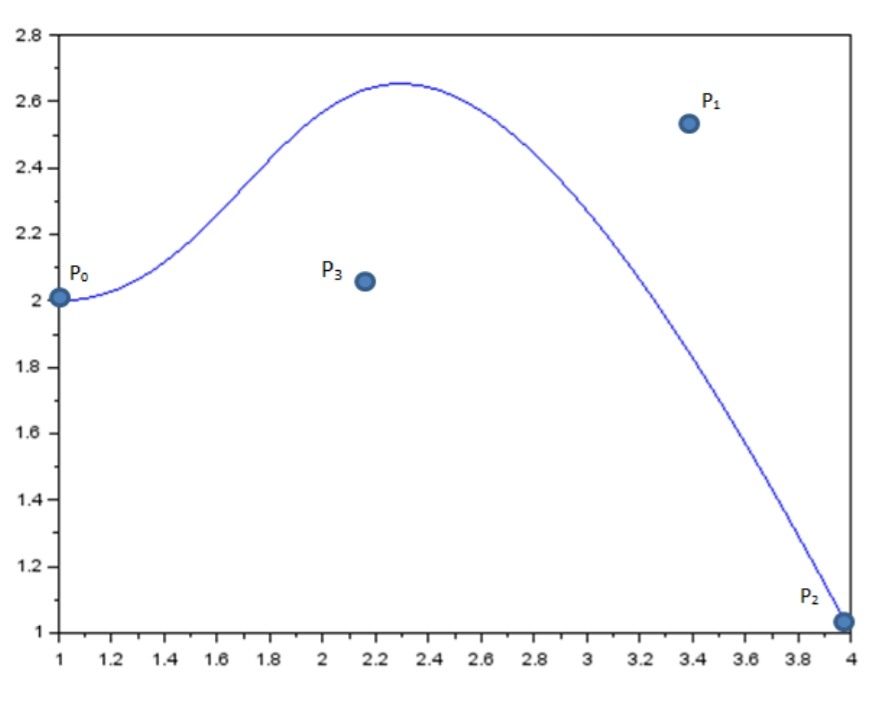
Рисунок 43 график кривой безье Р0,Р3,Р1,Р2
Вывод:
В ходе лабораторной работы получил базовые знания для работы в
двумерной и трехмерной графикой. В среде MATLAB/SCILAB, научился
создавать графики функций, построил поверхности, также использовал Мфайлы.








