Министерство науки и высшего образования

Министерство науки и высшего образования
Российской Федерации
федеральное государственное бюджетное образовательное учреждение
высшего образования
«Московский государственный технологический университет «СТАНКИН»
(ФГБОУ ВО «МГТУ «СТАНКИН»)
Институт автоматизации и робототехники
Кафедра робототехники и мехатроники
Дисциплина «Пакет прикладных программ Matlab для исследований и разработок»
ОТЧЁТ
по лабораторной работе
на тему:
Построение графиков функций в MATLAB/Scilab. Скрипты и функции
Выполнил:
студент группы АДБ-18-09 __________ _______ Сулаев Т.А.
(дата) (подпись) (ФИО)
Принял
преподаватель: __________ _______ Ким В. Л.
(дата) (подпись) (ФИО)
Оценка: ________ Дата:_________
Москва 2020
Цель работы: получение базовых знаний для работы c двумерной и
трёхмерной графикой в среде MATLAB, создание графиков функций одной
переменной, построение поверхностей, использование М-файлов, создание
пользовательских функций.
Задание №1
1.1. В интервале [0.1, 1] с шагом 0.1 рассчитать таблицу значений для
выражения из пункта №1 первой лабораторной работы, которое вы выбирали
согласно вашему варианту.
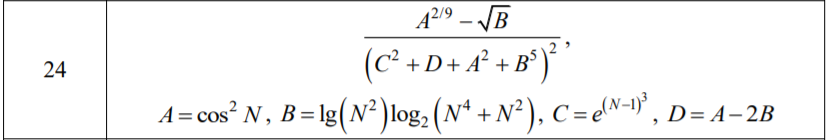
N=[0.1:0.1:1]// вектор N, которое изменяется в интервале 0.1-1 с шагом 0.1
N =
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.
A=cos(N)^2
A =
column 1 to 5
0.9900333 0.9605305 0.9126678 0.8483534 0.7701512
column 6 to 10
0.6811789 0.5849836 0.4854002 0.386399 0.2919266
B=log10(N^2).*log2(N^4 + N^2)
B =
column 1 to 5
13.259002 6.412732 3.5028725 1.9337747 1.0103
column 6 to 10
0.4571524 0.1405996 -0.0135363 -0.0505148 0.
--> C=exp(N - 1)
C =
column 1 to 5
0.4065697 0.449329 0.4965853 0.5488116 0.6065307
column 6 to 10
0.67032 0.7408182 0.8187308 0.9048374 1.
--> D=A - 2*B
D =
column 1 to 5
-25.52797 -11.864933 -6.0930772 -3.019196 -1.2504488
column 6 to 10
-0.233126 0.3037845 0.5124729 0.4874285 0.2919266
--> (A.^2.\9 - B.^1.\2).\(C.^2 + D + A.^2 + B.^5).^2
ans =
column 1 to 5
1.859D+10 12429739. 26662.912 54.673753 0.0441392
column 6 to 10
0.0326363 0.1182329 0.0108195 0.0212109 0.
1.2. Выполнить задание 1.1, используя шаг -0.1 начиная со значения N=1 до
N=0.
-> N=[1:-0.1:0]//вектор N, которое изменяется в интервале 0.1-1 с шагом 0.1
N =
1. 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.
--> A=cos(N)^2
A =
column 1 to 5
0.2919266 0.386399 0.4854002 0.5849836 0.6811789
column 6 to 11
0.7701512 0.8483534 0.9126678 0.9605305 0.9900333 1.
--> B=log10(N^2).*log2(N^4 + N^2)
B =
column 1 to 6
0. -0.0505148 -0.0135363 0.1405996 0.4571524 1.0103
column 7 to 11
1.9337747 3.5028725 6.412732 13.259002 Inf
--> C=exp(N - 1)
C =
column 1 to 6
1. 0.9048374 0.8187308 0.7408182 0.67032 0.6065307
column 7 to 11
0.5488116 0.4965853 0.449329 0.4065697 0.3678794
--> D=A - 2*B
D =
column 1 to 5
0.2919266 0.4874285 0.5124729 0.3037845 -0.233126
column 6 to 11
-1.2504488 -3.019196 -6.0930772 -11.864933 -25.52797 -Inf
--> (A.^2.\9 - B.^1.\2).\(C.^2 + D + A.^2 + B.^5).^2
ans =
column 1 to 6
0. 0.0212109 0.0108195 0.1182329 0.0326363 0.0441392
column 7 to 11
54.673753 26662.912 12429739. 1.859D+10 Nan
1.3. Отобразить в линейном масштабе на одних осях два графика функций с
помощью функции plot:
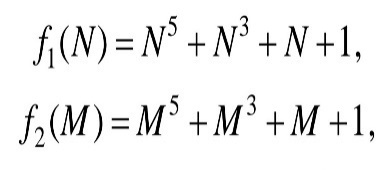
где N изменяется в диапазоне [0, 1] с шагом 0.1, а переменная M - с шагом
0.02.
Решение:
N=[0:0.1:1]
N =
0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.
--> M=[0:0.2:1]
M =
0. 0.2 0.4 0.6 0.8 1.
--> f1=N.^5+N.^3+N+1//ФУНКЦИЯ ВЕКТОРА N
f1 =
column 1 to 9
1. 1.10101 1.20832 1.32943 1.47424 1.65625 1.89376 2.21107 2.63968
column 10 to 11
3.21949 4.
--> f2=M.^5+M.^3+M+1//ФУНКЦИЯ ВЕКТОРА M
f2 =
1. 1.20832 1.47424 1.89376 2.63968 4.
--> plot(N,f1,'x-b')
--> plot(M,f2,'x-r')

Рисунок 1 два графика функций f1 и f2 с помощью функции plot
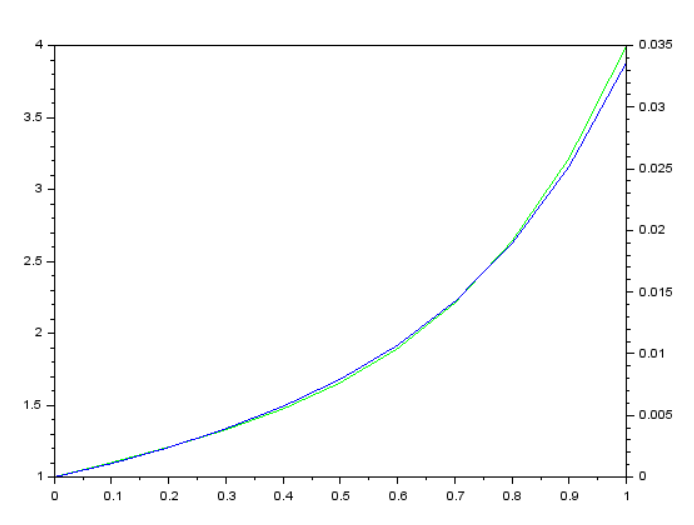
1.4. С помощью функции plot постройте графики функций f1(N) и 10-2
f1(N)*sin(N), так, чтобы отображались две оси с разным масштабом.
N=[0:0.1:1]
N =
0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.
--> f1=N.^5+N.^3+N+1
f1 =
column 1 to 9
1. 1.10101 1.20832 1.32943 1.47424 1.65625 1.89376 2.21107 2.63968
column 10 to 11
3.21949 4.
--> f2=10.^(-2).*f1.*sin(N)
f2 =
column 1 to 8
0. 0.0010992 0.0024006 0.0039287 0.005741 0.0079405 0.010693 0.0142441
column 9 to 11
0.0189359 0.0252191 0.0336588
--> na1=newaxes();//создает оси
--> plot(na1,N,f1,'y-g');//чертит первую функцию относительно оси
--> na2=newaxes();//создает вторую ось с новым масштаб
--> na2.filled="off";//не создает дополнительное окно
--> plot(na2,N,f2,);//чертит вторую функцию на том же окне
--> na2.axes_visible(1)="off";
--> na2.y_location="right";//сдвигает ось вправо
| 11 1 |
| 9 |
Рисунок 2 отображение двух осей с разными масштабами
1.5. Выполните задание 1.4, используя:
логарифмический масштаб по обеим осям;
логарифмический масштаб по оси абсцисс;
логарифмический масштаб по оси ординат.
//код 1
N=[0:0.1:1];
f1=N.^5+N.^3+N+1;
f2=10.^(-2).*f1.*sin(N);
na1=newaxes();
plot('ll',na1,N,f1,'colo','red','linest','-.','marker','>');//’ll’-логарифмический масштаб по обеим осям
красная штрихпунктирная линия и маркер- треугольник, указывающий вправо
na2=newaxes();
na2.filled="off";
plot('ll',na2,N,f2,'colo','blue','linest','--','marker','+');//’colo’-цвет, ‘linest’-тип линии, ‘marker’-
маркер, синяя штриховая линия и маркер- плюс
na2.axes_visible(1)="off";
na2.y_location="right";
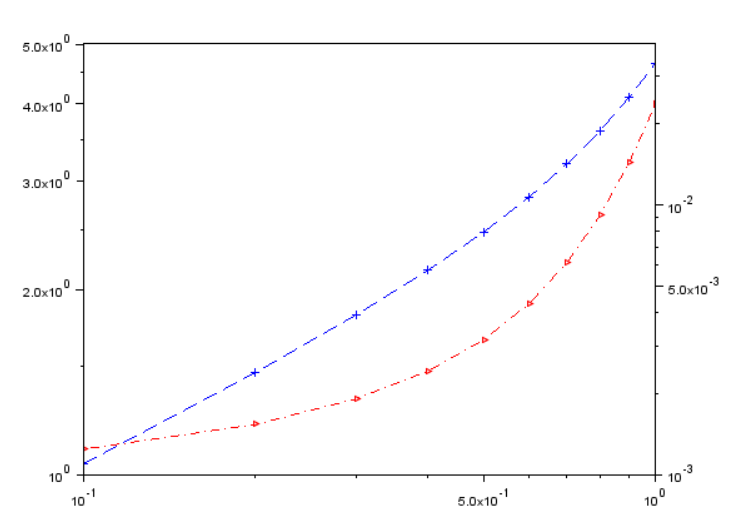
Рисунок 3 логарифмический масштаб по обеим осям
plot('ln',na1,N,f1,'colo','black','linest','-.','marker','P');//в предыдущем коде ‘ll’ заменяем ’ln’-
логарифмический масштаб по оси абсцисс, черная линия штрих пунктиром и маркер- пентаграмма
plot('ln',na2,N,f2,'colo','green','linest','-','marker','D');//зеленная сплошная линия и маркерромб
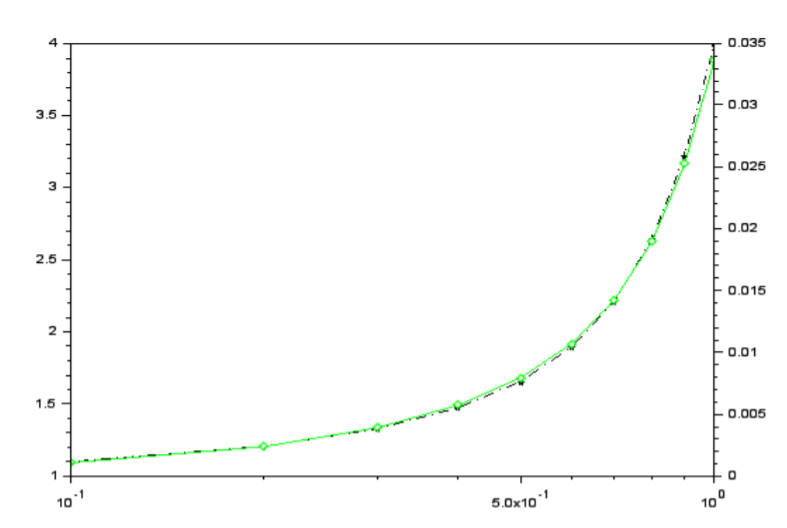
Рисунок 4 логарифмический масштаб по оси абсцисс
plot('nl',na1,N,f1,'colo','pink','linest','-','marker','*');//в коде 1 заменяем ‘ll’ на ‘nl’-
логарифмический масштаб по оси ординат, розовая сплошная линия и маркер- звездочка
plot('nl',na2,N,f2,'colo','gray','linest',':','marker','x');//серая пунктирная линия и маркер- крест
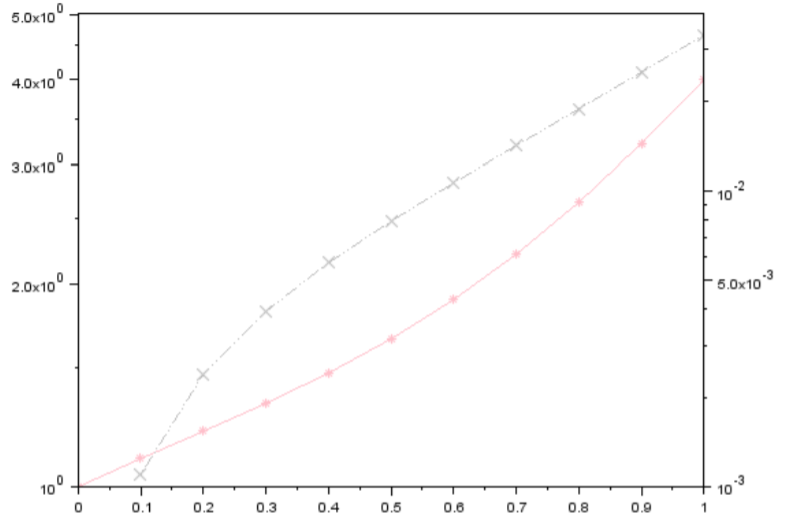
Рисунок 5 логарифмический масштаб по оси ординат
1.6. Сформируйте матрицу и вектор размерами соответственно не менее 5x6
и 1x7, первыми элементами которых является Ваш номер по списку в
журнале группы. Постройте графики вектора и матрицы. Примечание:
воспользуйтесь функциями Matplot и colorbar().
--> P=[2,3,4,5,6,7;2,3,4,5,6,7;2,3,4,5,6,7;2,3,4,5,6,7;2,3,4,5,6,7;]//матрица 5x6
P =
2. 3. 4. 5. 6. 7.
2. 3. 4. 5. 6. 7.
2. 3. 4. 5. 6. 7.
2. 3. 4. 5. 6. 7.
2. 3. 4. 5. 6. 7.
--> M=[2,3,4,5,6,7,8;]//вектор с размером 1x7
M =
2. 3. 4. 5. 6. 7. 8.
--> Matplot(P)// Matplot является листом иерархии графических функций. Он
представляет 2D-графики поверхности с использованием цветов и изображений. К
каждому цвету соответствует определенное число реализация матрицы Р
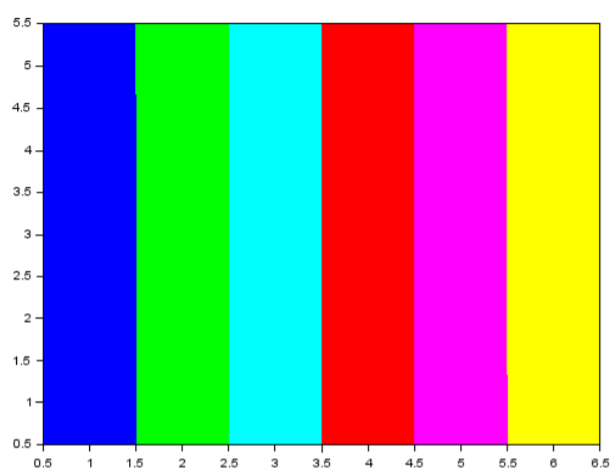
Рисунок 6 график матрицы5x6
--> colorbar//реализует цветную столбиковую диаграмму
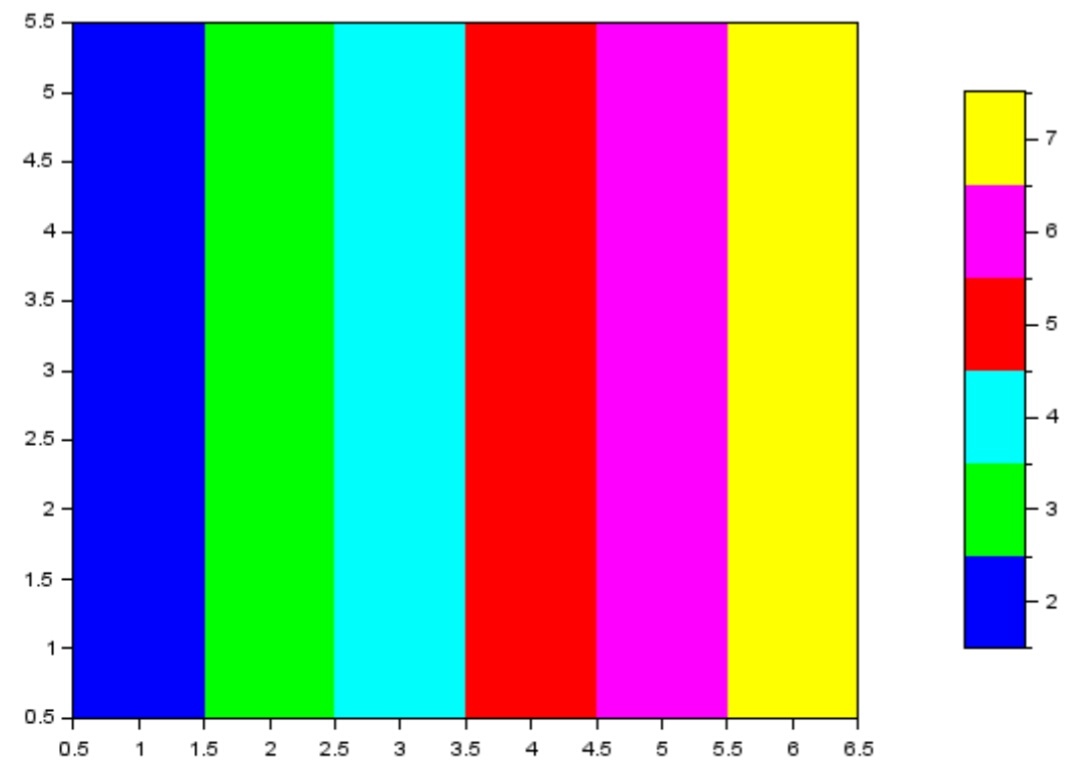
--> Matplot(M)//реализация вектора М
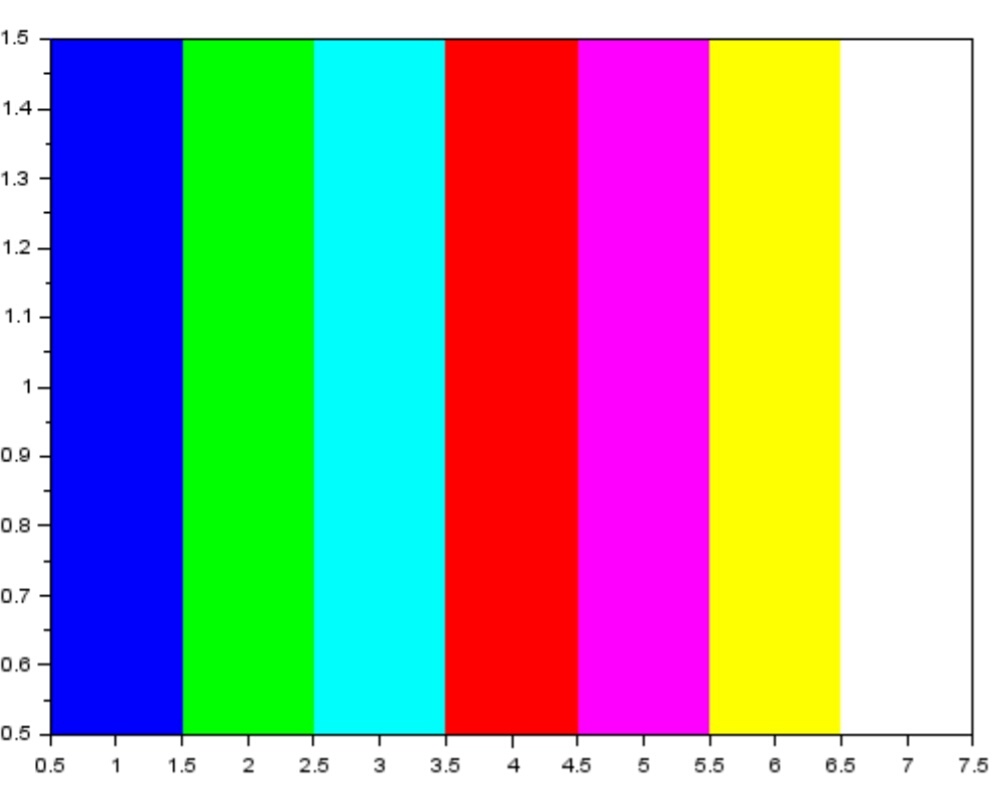
Рисунок 7 график вектора М
--> colorbar//реализация вектора М
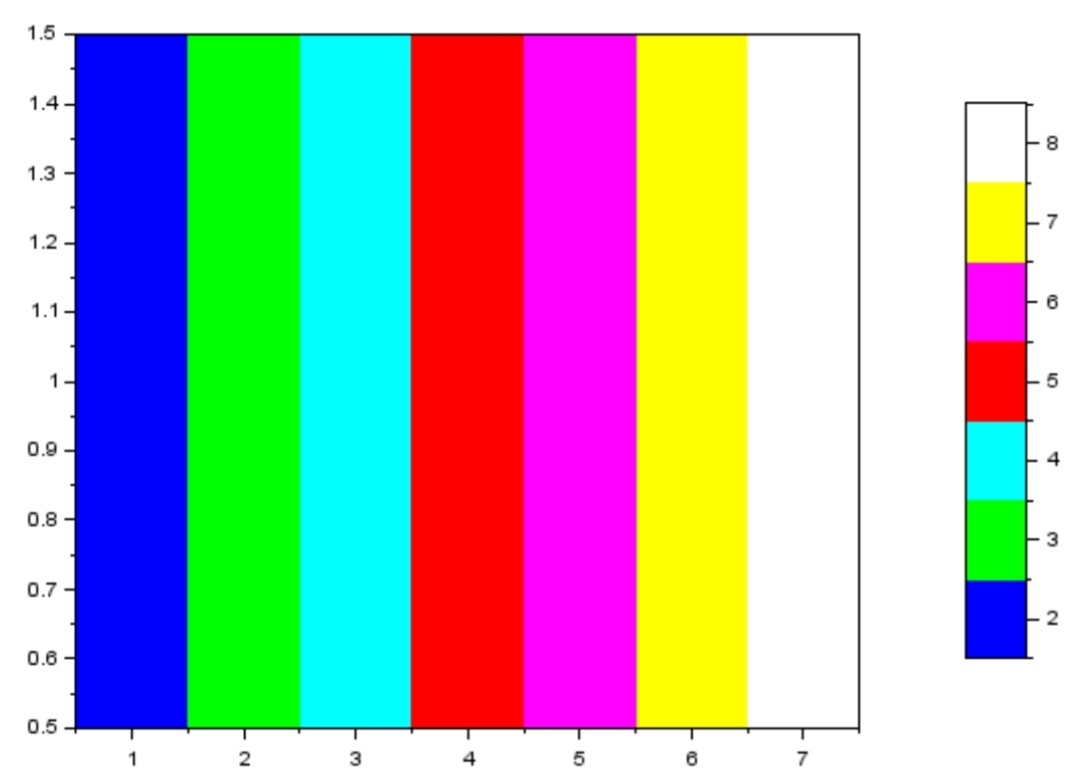
Рисуок 8 Результат использования функции colorbar








