Статистическая совокупность состоит из материально существующих объектов (работники, предприятия, страны, регионы) и является, в свою очередь, объектом статистического исследования.
Единица совокупности – каждая конкретная единица статистической совокупности.
Качественная однородность – сходство всех единиц совокупности по какому-либо признаку и несходство по всем остальным.
В статистической совокупности отличия одной единицы совокупности от другой чаще имеют количественную природу. Количественные изменения значений признака разных единиц совокупности называются вариацией.
Вариация признака – количественное изменение признака (для количественного признака) при переходе от одной единицы совокупности к другой.
Признак – это свойство, характерная черта или иная особенность единиц, объектов и явлений, которая может быть наблюдаема или измеряема. Признаки делятся на количественные и качественные. Многообразие и изменчивость величины признака у отдельных единиц совокупности называется вариацией.
Атрибутивные (качественные) признаки не поддаются числовому выражению (состав населения по полу). Количественные признаки имеют числовое выражение (состав населения по возрасту).
Показатель – это обобщающая количественно-качественная характеристика какого-либо свойства единиц или совокупности в целом в конкретных условиях времени и места.
Генеральная совокупность и выборка из нее. Основу статистического исследования составляет множество данных, полученных в результате измерения одного или нескольких признаков. Реально наблюдаемая совокупность объектов, статистически представленная рядом наблюдений 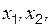 …,
…, 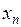 случайной величины
случайной величины 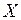 , является выборкой, а гипотетически существующая (домысливаемая) – генеральной совокупностью. Число наблюдений
, является выборкой, а гипотетически существующая (домысливаемая) – генеральной совокупностью. Число наблюдений 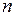 , образующих выборку, называется объемом выборки.
, образующих выборку, называется объемом выборки.
Основные способы организации выборки. Достоверность статистических выводов и содержательная интерпретация результатов зависит от репрезентативности выборки, т.е. полноты и адекватности представления свойств генеральной совокупности, по отношению к которой эту выборку можно считать представительной. Изучение статистических свойств совокупности можно организовать двумя способами: с помощью сплошного и несплошного наблюдения. Сплошное наблюдение предусматривает обследование всех единиц изучаемой совокупности, а несплошное (выборочное) наблюдение – только его части.
По методу отбора различают повторную и бесповторную выборку.
Так как выборочная совокупность отлична от генеральной, то возникают ошибки выборки.
При любом статистическом наблюдении (сплошном и выборочном) могут встретиться ошибки двух видов: регистрации и репрезентативности. Ошибки регистрации могут иметь случайный и систематический характер.
Случайные ошибки складываются из множества различных неконтролируемых причин, носят непреднамеренный характер и обычно по совокупности уравновешивают друг друга (например, изменения показателей прибора при температурных колебаниях в помещении).
Ошибки репрезентативности присущи только выборочному наблюдению, их невозможно избежать и они возникают в результате того, что выборочная совокупность не полностью воспроизводит генеральную. Значения показателей, получаемых по выборке, отличаются от показателей этих же величин в генеральной совокупности (или получаемых при сплошном наблюдении).
Ошибка выборочного наблюдения 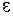 есть разность между значением параметра в генеральной совокупности и ее выборочным значением. Для среднего значения количественного признака
есть разность между значением параметра в генеральной совокупности и ее выборочным значением. Для среднего значения количественного признака 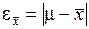 , а для доли (альтернативного признака)
, а для доли (альтернативного признака) 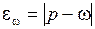 .
.
Ошибки выборки свойственны только выборочным наблюдениям. Чем значительнее эти ошибки, тем больше эмпирическое распределение отличается от теоретического. Параметры эмпирического распределения 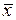 и
и 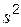 являются случайными величинами, следовательно, ошибки выборки также являются случайными величинами, могут принимать для разных выборок разные значения, и поэтому принято вычислять среднюю ошибку.
являются случайными величинами, следовательно, ошибки выборки также являются случайными величинами, могут принимать для разных выборок разные значения, и поэтому принято вычислять среднюю ошибку.
Средняя ошибка выборки есть величина 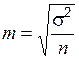 , выражающая среднее квадратическое отклонение выборочной средней от математического ожидания. Эта величина при соблюдении принципа случайного отбора зависит прежде всего от объема выборки
, выражающая среднее квадратическое отклонение выборочной средней от математического ожидания. Эта величина при соблюдении принципа случайного отбора зависит прежде всего от объема выборки 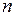 и от степени варьирования признака: чем больше
и от степени варьирования признака: чем больше 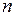 и чем меньше вариация признака (следовательно, и значение
и чем меньше вариация признака (следовательно, и значение 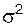 ), тем меньше величина средней ошибки выборки
), тем меньше величина средней ошибки выборки 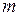 . Соотношение между дисперсиями генеральной и выборочной совокупностей выражается формулой
. Соотношение между дисперсиями генеральной и выборочной совокупностей выражается формулой
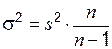 ,
,
т.е. при достаточно больших 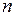 можно считать, что
можно считать, что 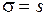 . Средняя ошибка выборки показывает возможные отклонения параметра выборочной совокупности от параметра генеральной. В табл. 3 приведены выражения для вычисления средней ошибки
. Средняя ошибка выборки показывает возможные отклонения параметра выборочной совокупности от параметра генеральной. В табл. 3 приведены выражения для вычисления средней ошибки 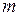 выборки при разных методах организации.
выборки при разных методах организации.
Таблица 3
Средняя ошибка выборки
| Вид выборки | Отбор | |
| повторный | бесповторный | |
| Количественный признак | ||
| Собственно-случайная | 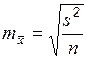
| 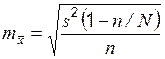
|
| Типическая (стратифицированная) | 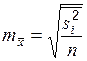
| 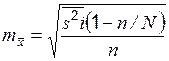
|
| Серийная | 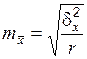
| 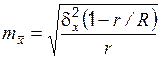
|
| Альтернативный признак | ||
| Собственно-случайная | 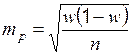
| 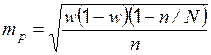
|
| Типическая (стратифицированная) | 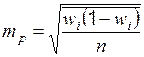
| 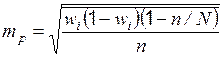
|
| Серийная | 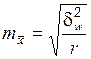
| 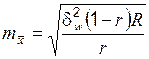
|
Задание 58. В одном из универмагов города с численностью работников 1000 человек было проведено 2%-ное выборочное обследование возраста работающих методом случайного бесповторного отбора.
В результате получены следующие данные.
| Возраст, лет | До 20 | 20–30 | 30–40 | 40–50 | Св. 50 |
| Число работников, чел. | 5 | 22 | 15 | 10 | 4 |
С вероятностью 0,997 установите пределы, в которых находится средний возраст работников универмага.
Задание 59. С чулочной фабрики на базу поступило 2 тыс. коробок чулок, упакованных по 20 пар в каждой коробке. Для проверки качества чулок методом механического отбора проверено 50 коробок. В результате проверки установлено, что 80 % чулок первого сорта. Дисперсия серийной выборки равна 16. С вероятностью 0,954 необходимо установить пределы, в которых находится доля чулок первого сорта в генеральной совокупности.
Задание 60. Из поступившей в продовольственный магазин партии было отобрано 400 изделий, 80 % из них соответствовали первому сорту. Определите среднюю ошибку выборки и границы, в которых находится доля изделий первого сорта во всей партии, с вероятностью 0,954.
Задание 61. В порядке случайной повторной выборки из партии было взято 100 проб сахара. В результате исследования установлена средняя влажность сахара в 9 % выборки при среднем квадратическом отклонении 1,55. С вероятностью 0,954 установите пределы, в которых находится средняя влажность сахара в партии.
Задание 62. По договоренности с поставщиком партия готовых изделий должна иметь не менее 90 % изделий первого сорта. При обследовании 900 единиц изделия первого сорта составили 82 %. С вероятностью 0,954 определите, соответствует ли партия готовых изделий предъявляемым требованиям.
Задание 63. Из поступившей в магазин партии костюмов в порядке собственно-случайного бесповторного отбора было отобрано 200, из которых 5 костюмов оказались бракованными. Можно ли с вероятностью 0,954 полагать, что брак во всей партии не превышает 5 %, если выборка составляет двадцатую часть ее размера.
Задание 64. В продовольственный магазин поступило 1000 ящиков с овощными консервами. В 100 обследованных в порядке бесповторного отбора ящиках оказалась бракованная продукция.
| % брака | Число ящиков |
| 1–2 | 50 |
| 2–3 | 25 |
| 3–4 | 8 |
Можно ли принять всю партию из 1000 ящиков при условии, что процент брака должен быть не больше 2,5 % с вероятностью 0,954?
Контрольные вопросы и задания
1. Дайте определение генеральной и выборочной совокупностей.
2. Вследствие чего образуются ошибки выборочного наблюдения?








