Средняя величина – это обобщающий показатель, который дает количественную характеристику признака в статистической совокупности в условиях конкретного места и времени.
Виды средних величин (табл. 1):
– степенные (гармоническая, геометрическая, арифметическая, квадратическая, кубическая, биквадратическая);
– структурные (мода, медиана, квартили, децили, квинтили, перцентили).
Таблица 1
Виды средних величин
| Вид степенной средней | Показатель степени средней k | Формула расчета | |
| простая | взвешенная | ||
| Гармоническая | –1 | 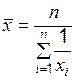
| 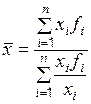
|
| Геометрическая | 1 | 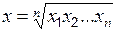
| 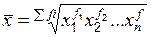
|
| Арифметическая | 0 | 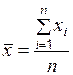
| 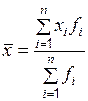
|
| Квадратическая | 2 | 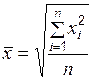
| 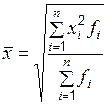
|
4.2. Мода и медиана
Мода – это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем – значение модальной величины признака по формуле
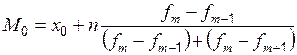 ,
,
где 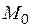 – значение моды;
– значение моды; 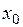 – нижняя граница модального интервала;
– нижняя граница модального интервала;
n – величина интервала; 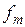 – частота модального интервала;
– частота модального интервала;
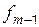 – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному; 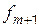 – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным.
Медиана – это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.
Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот 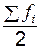 , а затем определяют, какое значение варианты приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле
, а затем определяют, какое значение варианты приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле
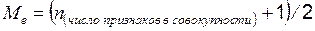 ,
,
в случае четного числа признаков медиана будет равна средней из двух признаков, находящихся в середине ряда).
При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем – значение медианы по формуле
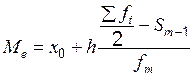 ,
,
где 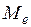 – искомая медиана;
– искомая медиана; 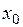 – нижняя граница интервала, который содержит медиану;
– нижняя граница интервала, который содержит медиану; 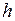 – величина интервала;
– величина интервала; 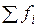 – сумма частот ряда;
– сумма частот ряда; 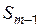 – сумма накопленных частот интервалов, предшествующих медианному;
– сумма накопленных частот интервалов, предшествующих медианному; 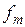 – частота медианного интервала.
– частота медианного интервала.
4.3. Показатели вариации
Вариация – это различия индивидуальных значений признака у единиц изучаемой совокупности. Исследование вариации имеет большое практическое значение и представляет собой необходимое звено в экономическом анализе. Важность изучения вариации связана с тем, что средняя, являясь равнодействующей, выполняет свою основную задачу с разной степенью точности: чем меньше различия индивидуальных значений признака, подлежащих осреднению, тем однороднее совокупность, а следовательно, точнее и надежнее средняя, и наоборот.
По степени вариации можно судить о границах вариации признака, однородности совокупности по данному признаку, типичности средней, взаимосвязи факторов, определяющих вариацию.
Изменение вариации признака в совокупности осуществляется с помощью абсолютных и относительных показателей.
Абсолютные показатели вариации включают (для несгруппированных и сгруппированных признаков):
– размах вариации 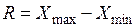 ;
;
– среднее линейное отклонение 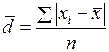 ,
, 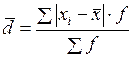 ;
;
– дисперсию 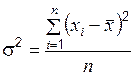 ,
, 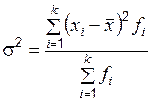 ;
;
– среднее квадратическое отклонение 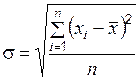 ,
, 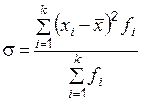 .
.
Относительные показатели вариации:
– коэффициент осцилляции 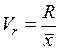 ;
;
– относительное линейное отклонение 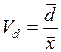 ;
;
– коэффициент вариации 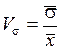 .
.
Все три дисперсии 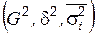 связаны между собой следующим равенством, которое известно как правило сложения дисперсий:
связаны между собой следующим равенством, которое известно как правило сложения дисперсий:
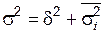 .
.
Межгрупповая дисперсия 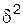 измеряет систематическую вариацию, обусловленную влиянием фактора, по которому произведена группировка:
измеряет систематическую вариацию, обусловленную влиянием фактора, по которому произведена группировка:
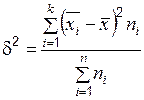 .
.
Внутригрупповая дисперсия оценивает вариацию признака, сложившуюся под влиянием других, не учитываемых в данном исследовании факторов, и не зависящую от фактора группировки. Она определяется как средняя из групповых дисперсий:
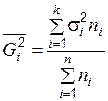 .
.
На этом соотношении строятся показатели, оценивающие влияние признака группировки на образование общей вариации. К ним относятся эмпирический коэффициент детерминации 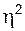 и эмпирическое корреляционное отношение
и эмпирическое корреляционное отношение 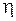 .
.
Задание 9. Имеются данные о заработной плате продавцов универмага.
| Заработная плата за месяц | До 5000 | 5000– 7200 | 7200– 9400 | 9400– 12 000 | 12 000– 13500 | 13 500– 15 000 | Свыше 15 000 |
| Число продавцов | 10 | 16 | 21 | 45 | 32 | 19 | 8 |
Определите среднюю зарплату продавца.
Задание 10. Имеются данные по трем магазинам объединения «Вернисаж» за месяц.
| № магазина | Средняя зарплата продавца, р. | Фонд оплаты труда продавцов, р. | Средняя выработка на одного продавца, тыс. р. |
| 1 | 10 025 | 70 250 | 12,5 |
| 2 | 9880 | 47 904 | 12,2 |
| 3 | 10 860 | 43 032 | 13,1 |
Определите количество продавцов, среднюю выработку и среднюю заработную плату по объединению «Вернисаж».
Задание 11. По данным о цене и объеме продажи творога на трех рынках города определите среднюю цену 1 кг творога за I квартал, за
II квартал и за полугодие.
| № п/п | Рынок | I квартал | II квартал | ||
| Цена за 1 кг, р. | Продано, кг | Цена за 1 кг, р. | Продано на сумму, р. | ||
| 1 | Центральный | 188 | 50 | 200 | 12 040 |
| 2 | Северный | 175 | 45 | 195 | 12 100 |
| 3 | Южный | 170 | 60 | 170 | 11 650 |
Задание 12. Имеются данные о распределении магазинов по размеру товарооборота.
| Группа магазинов по размеру месячного товарооборота, тыс. р. | До 10 | 10–20 | 20–30 | 30–40 | 40–50 | Свыше 50 |
| Число магазинов, % к итогу | 5 | 15 | 23 | 27 | 16 | 14 |
Определите:
1) средний товарооборот, приходящийся на один магазин;
2) моду и медиану.
Задание 13. Имеются данные о распределении продавцов торгового объединения по возрасту.
| Возраст продавцов | До 18 | 18–28 | 28–38 | 38–48 | Свыше 48 |
| Число продавцов | 17 | 38 | 72 | 49 | 24 |
Определите:
1) средний возраст продавца;
2) моду и медиану;
3) показатели вариации:
– размах вариации;
– среднее линейное отклонение;
– средний квадрат отклонений (дисперсию);
– среднее квадратическое отклонение;
– коэффициент вариации.
Сделайте выводы.
Задание 14. Имеются результаты группировки магазинов по расстоянию от базы снабжения.
| Расстояние от базы снабжения, км | До 10 | 10–20 | 20–30 | 30–40 | 40–50 | Свыше 50 |
| Число магазинов, ед. | 9 | 22 | 26 | 20 | 13 | 10 |
Определите:
1) среднее расстояние от базы снабжения, км;
2) моду и медиану;
3) показатели вариации:
– размах вариации;
– среднее линейное отклонение;
– средний квадрат отклонений (дисперсию);
– среднее квадратическое отклонение;
– коэффициент вариации.
Сделайте выводы.
Задание 15. Имеются данные о размере товарооборота продовольственных магазинов города.
| Группа магазинов по размеру товарооборота, тыс. р. | 1000– 1050 | 1100– 1150 | 1150– 1200 | 2000– 1250 | 1250– 1300 | 1300– 1350 | 1400– 1450 | 1450– 1500 | Свыше 1500 |
| Число магазинов | 2 | 16 | 35 | 51 | 43 | 26 | 8 | 6 | 3 |
Определите средний товарооборот и среднее квадратическое отклонение товарооборота по магазинам города способом моментов.
Задание 16. Имеются данные по трем секциям универмага.
| Стаж работы (лет) | Число продавцов | Средняя зарплата | Среднее квадратическое зарплаты, р. |
| До 3 | 12 | 10 000 | 15 |
| 3–10 | 10 | 12 000 | 12 |
| Более 10 | 15 | 14 000 | 22 |
Рассчитайте:
1) среднюю зарплату продавцов универмага;
2) общую дисперсию и среднее квадратическое отклонение заработной платы продавцов.
Задание 17. Имеются данные по десяти продовольственным магазинам города.
| № магазина | Товарооборот, млн. р. | Количество розничных торговых предприятий | Прибыль, тыс. р. |
| 1 | 3,8 | 5 | 51 |
| 2 | 1,9 | 4 | 19 |
| 3 | 4,4 | 6 | 83 |
| 4 | 4,4 | 6 | 49 |
| 5 | 2,4 | 5 | 25 |
| 6 | 3,2 | 5 | 38 |
| 7 | 4,6 | 8 | 51 |
| 8 | 5,0 | 8 | 60 |
| 9 | 2,8 | 6 | 21 |
| 10 | 3,9 | 5 | 40 |
Вычислите дисперсию и среднее квадратическое отклонение, применив формулу 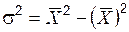 :
:
1) по товарообороту;
2) по количеству розничных предприятий;
3) по прибыли расчетной и фактической;
4) по расстоянию от базы снабжения.
Задание 18. Определите среднее квадратическое отклонение, если известно, что средняя величина признака – 240, а коэффициент вариации составляет 31 %.
Задание 19. Средняя величина признака равна 25, а коэффициент вариации 30 %. Определите дисперсию.
Задание 20. Дисперсия признака равна 60 000, коэффициент вариации 33 %, определите среднюю величину признака.
Задание 21. Средняя величина признака равна 13, а дисперсия – 174. Определите коэффициент вариации.
Задание 22. Дисперсия признака равна 25. Средний квадрат его индивидуальных значений равен 250. Определите среднюю величину признака.
Задание 23. Средняя величина признака в совокупности равна 15, средний квадрат отклонений индивидуальных значений признака от этой средней равен 25. Определите средний квадрат отклонений индивидуальных значений этого признака: а) от 20; б) от 10.
Задание 24. Средний квадрат отклонений вариантов признака от произвольной величины 30 равен 136, средняя величина равна 20.
Определите среднее квадратическое отклонение вариантов признака от их средней величины.
Задание 25. Средний квадрат отклонений вариантов признака от некоторой произвольной величины равен 500, а разность между этой произвольной величиной и средней равна 14. Определите дисперсию и среднее квадратическое отклонение.
Задание 26. Средний квадрат отклонений от произвольной величины равен 300. Эта величина больше средней на 12 единиц. Определите дисперсию.
Задание 27. Имеются данные о производительности труда 10 продавцов разных секций.
| Секция «Галантерея» | Секция «Парфюмерия» | ||
| № п/п | Товарооборот за месяц, тыс. р. | № п/п | Товарооборот за месяц, тыс. р. |
| 1 | 20 | 6 | 30 |
| 2 | 25 | 7 | 30 |
| 3 | 20 | 8 | 35 |
| 4 | 20 | 9 | 40 |
| 5 | 25 | 10 | 30 |
Вычислите:
1) средний товарооборот для первой и второй секции и для двух секций в целом;
2) групповые дисперсии;
3) среднюю из групповых дисперсий;
4) дисперсию групповых средних;
5) общую дисперсию (по правилу сложения дисперсий);
6) эмпирическое корреляционное отношение.
Задание 28. Имеются данные о заработной плате работников торговли.
| Группа торговых работников по размеру зарплаты, р. | 800–1000 | 1000–1200 | 1200–1400 | 1400–1600 | 1600–1800 | 1800–2000 |
| Число работников | 20 | 80 | 160 | 90 | 40 | 10 |
Определите дисперсию зарплаты работников торговли способом моментов.
Контрольные вопросы и задания
1. Дайте определение понятия средних величин в рядах распределения. Укажите виды средних и способы их вычисления.
2. Охарактеризуйте структурные средние: моду и медиану, квартили и децили.
3. В чем сущность понятия вариации? Каковы виды вариационных рядов? Назовите показатели вариации.
4. Что представляет собой дисперсия альтернативного признака?
Каковы математические свойства дисперсии?
5. Сформулируйте закон сложения (разложения) вариации и дисперсии. Каковы особенности применения дисперсии для оценки степени взаимосвязей социально-экономических явлений (коэффициент детерминации, эмпирическое корреляционное отношение)?
5. РЯДЫ ДИНАМИКИ
Абсолютные приросты 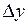 показывают, на сколько единиц изменился последующий уровень ряда по сравнению с предыдущим. Формулы расчета можно записать следующим образом:
показывают, на сколько единиц изменился последующий уровень ряда по сравнению с предыдущим. Формулы расчета можно записать следующим образом:
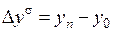 ;
;
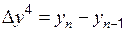 ,
,
где 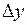 – абсолютный прирост (
– абсолютный прирост ( 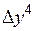 – цепной;
– цепной; 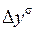 – базисный);
– базисный);
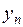 – уровень ряда за отчетный период;
– уровень ряда за отчетный период; 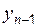 – уровень ряда предыдущего периода;
– уровень ряда предыдущего периода; 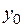 – уровень ряда начальный.
– уровень ряда начальный.
При уменьшении абсолютных значений ряда будет соответственно «уменьшение», или «снижение».
Коэффициент роста показывает, во сколько раз изменился уровень ряда по сравнению с предыдущим или по сравнению с начальным уровнем. Формулы расчета можно записать следующим образом:
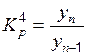 ;
; 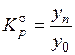 .
.
Темпы роста показывают, сколько процентов составляет последующий уровень ряда по сравнению с предыдущим или по сравнению с начальным уровнем. Формулы расчета можно записать следующим образом:
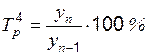 или
или 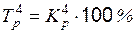 .
.
Темпы прироста показывают, на сколько процентов увеличился уровень отчетного периода по сравнению с предыдущим или по сравнению с начальным уровнем. Формулы расчета можно записать следующим образом:
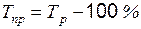 или
или 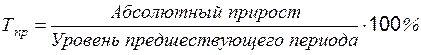 .
.
Если абсолютные уровни в ряду уменьшаются, то темп будет меньше 100 % и соответственно будет темп снижения (темп прироста со знаком минус).
Абсолютное значение 1 % прироста показывает, сколько единиц надо произвести в данном периоде, чтобы уровень предыдущего периода возрос на 1 %.
Определить величину абсолютного значения 1 % прироста можно двумя способами:
§ уровень предшествующего периода разделить на 100;
§ цепные абсолютные приросты разделить на соответствующие цепные темпы прироста.
Абсолютное значение 1 % прироста = 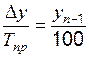 .
.
Среднегодовой темп роста исчисляется в нижеприведенной последовательности:
1) сначала по формуле средней геометрической исчисляют среднегодовой коэффициент роста (снижения) 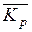 ;
;
2) на базе среднегодового коэффициента определяют среднегодовой темп роста 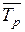 путем умножения коэффициента на 100 %:
путем умножения коэффициента на 100 %:
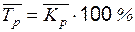 .
.
Среднегодовой темп прироста определяется путем вычитания из темпа роста 100 %:
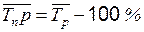 .
.
Среднегодовой коэффициент роста (снижения) по формулам средней геометрической может быть исчислен двумя способами:
1) на базе абсолютных показателей ряда динамики по формуле (например)
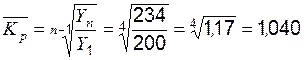 ,
,
где n – число уровней; n – 1 – число лет в периоде;
2) на базе ежегодных коэффициентов роста по формуле (например)
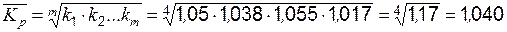 .
.
Задание 29. Имеются данные о розничном товарообороте продовольственного магазина, тыс. р.
| Показатель | Годы | |||||
| 1-й | 2-й | 3-й | 4-й | 5-й | 6-й | |
| Розничный товарооборот, включая стоимость упаковки | 350 | 467 | 325 | – | – | – |
| Розничный товарооборот без стоимости упаковки | – | – | 317 | 402 | 387 | 415 |
1. Установите причины несопоставимости ряда динамики для сравнительного анализа.








