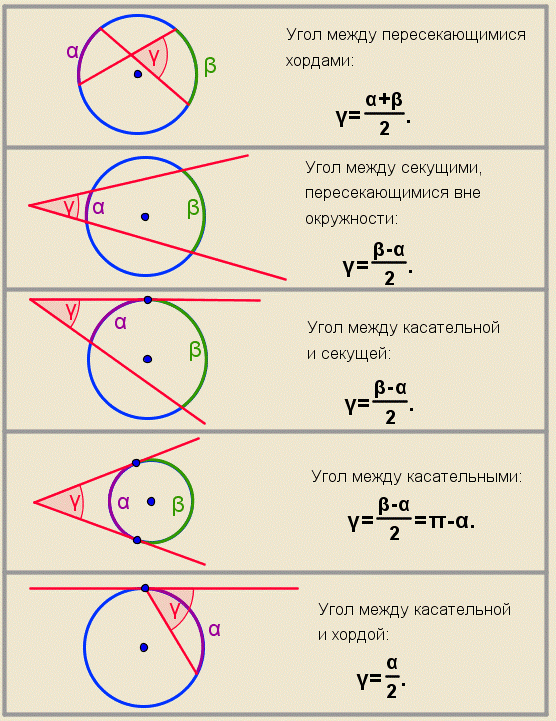
Вписанная окружность
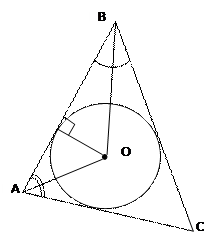
| В любой треугольник можно вписать окружность.
Её центр – точка пересечения биссектрис треугольника.
r = 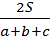 - радиус вписанной окружности
a , b , c – стороны треугольника
S – площадь треугольника - радиус вписанной окружности
a , b , c – стороны треугольника
S – площадь треугольника
|
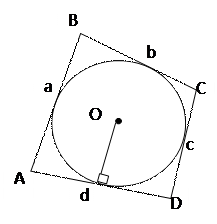
| В выпуклый четырехугольник можно вписать окружность, только если: a + c = b + d , где a , b , c , d- стороны четырехугольника |
ОПИСАННАЯ ОКРУЖНОСТЬ
|
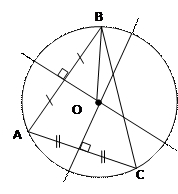
Около любого треугольника можно описать окружность.
Её центр – точка пересечения серединных перпендикуляров к сторонам треугольника.
R = 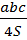 - радиус описанной окружности
a , b , c – стороны треугольника
S – площадь треугольника - радиус описанной окружности
a , b , c – стороны треугольника
S – площадь треугольника
|
|
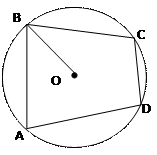
Около выпуклого четырехугольника можно описать окружность, только если:
 A + A +  С = С =  В + В +  D = 180° D = 180°
|
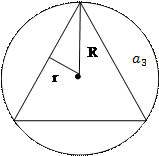
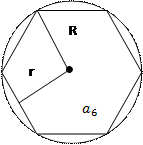
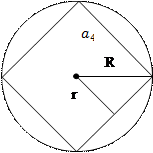
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ
Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
 | |||||
 | |||||
 | |||||
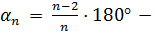 вычисление угла многоугольника
вычисление угла многоугольника
а n 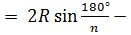 сторона многоугольника
сторона многоугольника
S = 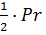 - площадь
- площадь
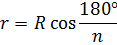
n – число сторон
R – радиус описанной окружности
r – радиус вписанной окружности
Р – периметр
треугольник
|  квадрат квадрат
|  шестиугольник шестиугольник
| |
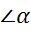
| 60° | 90° | 120° |
| а | 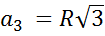
| 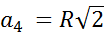
| 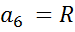
|
| R | R = 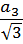
| R = 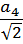
| 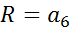
|
| r | r =  R R
| r = 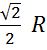
| r = 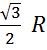
|
ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ
| Расстояние между точками | А(х1; у1) и В(х2; у2)
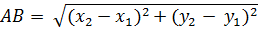
|
| Координаты (х; у) середины отрезка АВ с концами А(х1; у1) и В(х2; у2) |
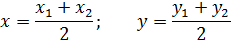
|
Общее уравнение прямой, перпендикулярной вектору 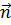 {a; b} {a; b}
|
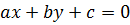
|
| Уравнение окружности с радиусом R и с центром в точке (х0; у0) |
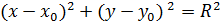
|
Если А(х1; у1) и В(х2; у2), то координаты вектора 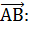
| 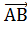 {х2-х1; у2-у1} {х2-х1; у2-у1}
|
| Сложение векторов | 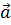 {а1; а2} + {а1; а2} + 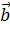 {b1; b2} = {b1; b2} = 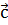 {a1 + b1; a2 + b2} {a1 + b1; a2 + b2}
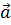 {а1; а2} {а1; а2} 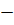 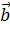 {b1; b2} = {b1; b2} = 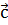 {a1 {a1 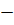 b1; a2 b1; a2 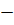 b2} b2}
|
Умножение вектора 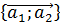 на
число на
число 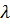
| 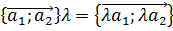
|
Скалярное произведение векторов:
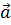 и и 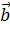
| 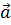 ∙ ∙ 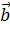 = = 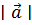 ∙∣ ∙∣ 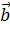 ∣∙ ∣∙ 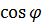 где
где 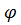 - угол между векторами - угол между векторами 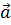 и и 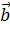
|
| Скалярное произведение векторов | 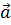 {а1; а2} и {а1; а2} и 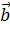 {b1; b2} {b1; b2}
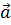 ∙ ∙ 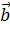 = a1b1 + a2b2 = a1b1 + a2b2
|
Косинус угла между векторами: 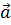 {а1; а2} и {а1; а2} и 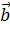 {b1; b2} {b1; b2}
| 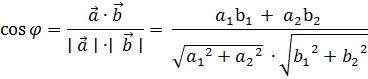
|
| Необходимое и достаточное условие перпендикулярности векторов | 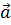 {a1; а2} {a1; а2}   {b1; b2} {b1; b2}
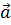 ∙ ∙ 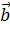 = 0 или a1b1 + a2b2 = 0 = 0 или a1b1 + a2b2 = 0
|