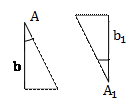
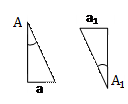
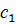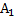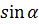7. Прямоугольный треугольник. Основные соотношения ……. 9
Справочник по геометрии 7-9
ОГЛАВЛЕНИЕ
стр.
1. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ. АКСИОМЫ ………………………………... 3
2. УГЛЫ. БИССЕКТРИСА УГЛА ……………………………………………….... 4
3. ВИДЫ ТРЕУГОЛЬНИКОВ. СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ
И УГЛАМИ ТРЕУГОЛЬНИКА …………………………………………………... 5
4. ПЛОЩАДЬ ТРЕУГОЛЬНИКА. СВОЙСТВА РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА ……..………………………………………………………............ 6
5. ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ. ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ ……………………………………………………………………. 7 6. ЗАМЕЧАТЕЛЬНЫЕ ЛИНИИ В ТРЕУГОЛЬНИКЕ ……………………………….. 8
7. ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК. ОСНОВНЫЕ СООТНОШЕНИЯ ……. 9
8. СВОЙСТВА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА. ПРИЗНАКИ
РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ …………………………. 10
9. ЗНАЧЕНИЯ СИНУСА, КОСИНУСА И ТАНГЕНСА НЕКОТОРЫХ УГЛОВ. ЧЕТЫРЕХУГОЛЬНИКИ ……………………….……………………………………... 11
10. СВОЙСТВА И ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА ……………………… 12
11. ПРЯМОУГОЛЬНИК. РОМБ. КВАДРАТ ……………………………………… 13
12. ТРАПЕЦИЯ …………………………………………………………………….. 14
13. ОКРУЖНОСТЬ. ВПИСАННЫЙ УГОЛ ………………………………………. 15
14. СВОЙСТВА ОКРУЖНОСТИ И ЕЕ ЭЛЕМЕНТОВ ………………………….. 16
15. СВОЙСТВА КАСАТЕЛЬНЫХ И СЕКУЩИХ ………………………………… 17
16. ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ ……………………………. 18
17. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ ……………………………………….. 19
18. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ. ВЕКТОРЫ. ……………….. 20
Справочник по геометрии 7-9
ПАРАЛЛЕЛЬНОСТЬ
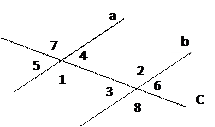 Прямые а и b пересечены секущей с
Прямые а и b пересечены секущей с
 1 и
1 и  2;
2; 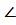 3 и
3 и 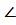 4 – накрест лежащие углы
4 – накрест лежащие углы
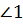 и
и  8;
8;  3 и
3 и  5 - соответственные углы
5 - соответственные углы
 2 и
2 и  7;
7;  4 и
4 и  6 - соответственные углы
6 - соответственные углы
 1 и
1 и 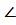 3;
3; 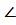 2 и
2 и  4 - односторонние углы
4 - односторонние углы
Признаки параллельности прямых
 1= 1=  2 2 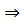 а║b
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны. а║b
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
 1 = 1 =  8 8 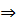 а║ b
Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны. а║ b
Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
 1 + 1 +  3= 3= 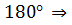 а║ b
Если при пересечении двух прямых секущей сумма односторонних углов равна 180º, то прямые параллельны.
а║ b , а║с а║ b
Если при пересечении двух прямых секущей сумма односторонних углов равна 180º, то прямые параллельны.
а║ b , а║с 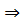 с║ b а с║ b а 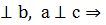 с║ b с║ b
| Свойства углов при параллельных прямых
а║ b 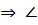 1 = 1 =  2
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
а║ b 2
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
а║ b 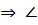 1 = 1 =  8
Если две параллельные прямые пересечены секущей, то соответственные углы равны.
а║ b 8
Если две параллельные прямые пересечены секущей, то соответственные углы равны.
а║ b 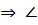 1 + 1 +  3= 3= 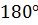 Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна
Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 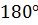 . .
|
НЕКОТОРЫЕ АКСИОМЫ ПЛАНИМЕТРИИ
Через любые две различные точки проходит прямая, и притом только одна.
А |  Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
а║ b А Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
а║ b А 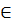 а а
|
УГЛЫ
Острый угол
меньше прямого угла
| Тупой угол
больше прямого угла
| Прямой угол
| Развернутый угол

 AOM = AOM = 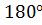
| |||||||||
| Смежные углы
|
Сумма смежных углов рав
| |||||||||||
|
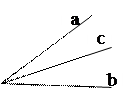
Вертикальные углы
|
Вертикальные углы равны. | |||||||||||
БИССЕКТРИСА УГЛА
|
с – биссектриса  ab ab
 a с = a с =  с b
Луч с делит угол с b
Луч с делит угол 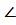 ab пополам ab пополам
| |||
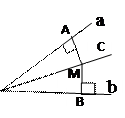
| Свойство биссектрисы
АМ = ВМ
 Каждая точка биссектрисы
неразвернутого угла равноудалена от сторон угла. Каждая точка биссектрисы
неразвернутого угла равноудалена от сторон угла.
|
ВИДЫ ТРЕУГОЛЬНИКОВ
| Треугольник | Разносторонний | Равнобедренный | Равносторонний | |||
| Остроугольный (все углы острые) |  все стороны разной длины
все стороны разной длины
|  две стороны равны
две стороны равны
| 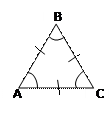 все стороны равны
все стороны равны
| |||
| Прямоугольный (один из углов – прямой) |
| 
|
∠ А=
Р = 3а, где а - сторона, Р- периметр | |||
| Тупоугольный (один из углов – тупой) | 
| 
|
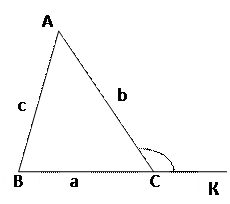
СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ТРЕУГОЛЬНИКА
|
| Сумма углов треугольника равна 180 ̊.
∠ А+  В+ В+ 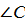 =180 ̊
Свойство внешнего угла: ∠ АСК = ∠ А + =180 ̊
Свойство внешнего угла: ∠ АСК = ∠ А +  В В
|
| Неравенство треугольника а < b +с b < а+с с < а+ b Каждая сторона треугольника меньше суммы двух других сторон. а > b - с, где b >с | |
Теорема о соотношениях между сторонами и углами треугольника
b > с 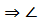 В > В >  С и С и  В > В >  С С 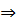 b > с
В треугольнике против большей стороны лежит больший угол.
Против большего угла лежит большая сторона. b > с
В треугольнике против большей стороны лежит больший угол.
Против большего угла лежит большая сторона.
| |
Теорема синусов
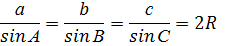 где
где 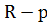 адиус описанной окружности.
Стороны треугольника пропорциональны синусам противолежащих углов. адиус описанной окружности.
Стороны треугольника пропорциональны синусам противолежащих углов.
| Теорема косинусов
с² = а² + b ² ― 2а b 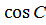 а² = с² + b ² ― 2 b с
а² = с² + b ² ― 2 b с 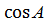 b ² = с² + а²― 2 ас
b ² = с² + а²― 2 ас 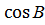 Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
|
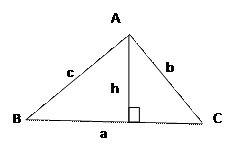
ПЛОЩАДЬ ТРЕУГОЛЬНИКА
Площадь треугольника равна половине произведения его стороны на высоту к этой стороне: S = | Другие формулы:
S = 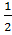 ab ab 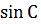 = =  a с a с 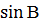 = =  с b с b 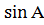 S =
S = 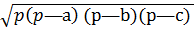 ,
где ,
где 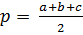 - полупериметр
S = - полупериметр
S = 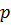 r ,
где r- радиус вписанной в треугольник окружности
S = r ,
где r- радиус вписанной в треугольник окружности
S = 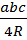 ,
где R – радиус описанной окружности ,
где R – радиус описанной окружности
|
СВОЙСТВА РАВНОБЕДРЕНННОГО ТРЕУГОЛЬНИКА
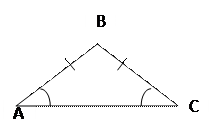 В равнобедренном треугольнике углы при основании равны В равнобедренном треугольнике углы при основании равны
 А = А =  С С  АС – основание
АВ и ВС – боковые стороны
АС – основание
АВ и ВС – боковые стороны
|
Биссектриса, проведенная к основанию, является медианой и высотой
ВК – биссектриса ВК – медиана ВК - высота |
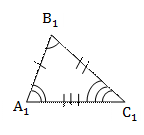
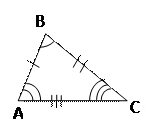
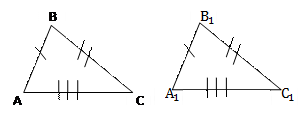
РАВНЫЕ И ПОДОБНЫЕ ТРЕУГОЛЬНИКИ
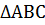 = = 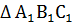 , значит,
АВ = , значит,
АВ = 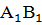 СВ = СВ = 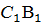 СА = С1А1 СА = С1А1
 А = А =  А1 А1  В = В = 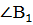  С = С =  С1. С1.
| 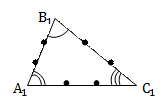 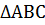 подобен подобен 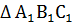 , значит, , значит,  А = А =  А1 А1  В = В = 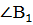  С = С =  С1 С1
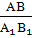 = = 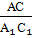 = = 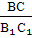
| |||||||||||
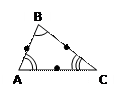
| ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ | ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ | |||||||||||
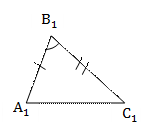 По двум сторонам и углу между ними По двум сторонам и углу между ними
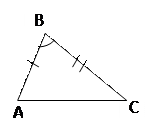 АВ =
АВ = 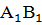 СВ = СВ = 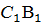  В = В = 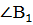
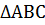 = = 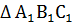 Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
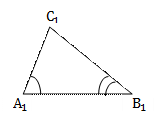
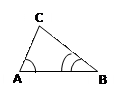
| По двум углам
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны. | |||||||||||
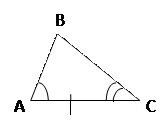 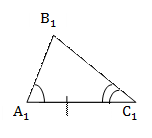 По стороне и двум прилежащим углам
АС= По стороне и двум прилежащим углам
АС= 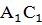  А = А = 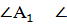 С = С = 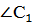
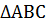 = = 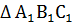 Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
| 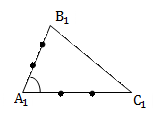 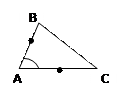 По двум сходственным сторонам и углу между ними По двум сходственным сторонам и углу между ними
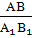 = = 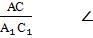 А = А = 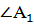
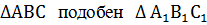 Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
| |||||||||||
По трем сторонам
АВ =
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны. | 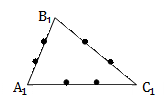 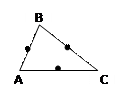 По трем сходственным сторонам По трем сходственным сторонам
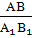 = = 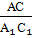 = = 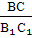
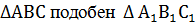 Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
| |||||||||||
ЗАМЕЧАТЕЛЬНЫЕ ЛИНИИ В ТРЕУГОЛЬНИКЕ
|
АМ – медиана  АВС
точка М – середина ВС АВС
точка М – середина ВС
| ||||||||||||
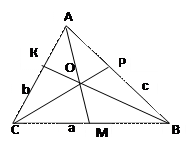
| Свойство медиан
СО:ОР = АО:ОМ = ВО:ОК = 2:1
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1.
АМ = m 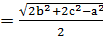 формула для вычисления медианы
формула для вычисления медианы
| ||||||||||||
|
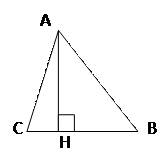
АН – высота 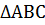 АН - перпендикуляр, опущенный из
точки А на прямую ВС
Свойство высот
Высоты треугольника пересекаются в одной точке треугольника.
АН - перпендикуляр, опущенный из
точки А на прямую ВС
Свойство высот
Высоты треугольника пересекаются в одной точке треугольника.
| ||||||||||||
.
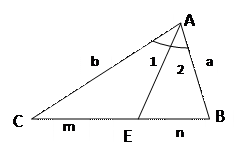
| АЕ – биссектриса 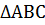
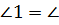 2 ( 2 (  САЕ = САЕ =  ВАЕ)
Свойства биссектрисы треугольника
Биссектрисы треугольника пересекаются в одной точке (центре вписанной окружности).
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника. ВАЕ)
Свойства биссектрисы треугольника
Биссектрисы треугольника пересекаются в одной точке (центре вписанной окружности).
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
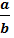 = = 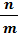
| ||||||||||||

|
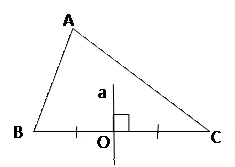
Прямая а – серединный перпендикуляр
О 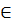 а ОС = ОВ а а ОС = ОВ а  ВС
Свойство серединных перпендикуляров
Серединные перпендикуляры пересекаются в одной точке (центре описанной окружности) ВС
Свойство серединных перпендикуляров
Серединные перпендикуляры пересекаются в одной точке (центре описанной окружности)
| ||||||||||||
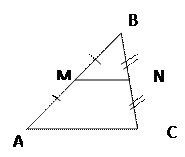
| MN – средняя линия  точка М - середина АВ, N – середина ВС
Свойство средней линии треугольника
MN
точка М - середина АВ, N – середина ВС
Свойство средней линии треугольника
MN  АС; MN = АС; MN = 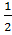 АС
Средняя линия параллельна одной из сторон и равна её половине. АС
Средняя линия параллельна одной из сторон и равна её половине.
| ||||||||||||
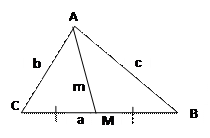
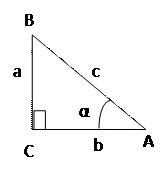
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
| Основные соотношения в прямоугольном треугольнике | ||||||||||||||||
|
|
Теорема Пифагора c²=а² + b² Квадрат гипотенузы равен сумме квадратов катетов.
|
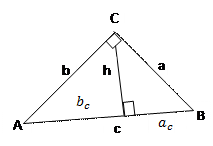
Пропорциональные отрезки h ² = а² = b² = h | ||||||||||||||
|
с = АВ – гипотенуза а = ВС – катет, противолежащий к α b = АС – катет, прилежащий к углу α | СИНУС Отношение противолежащего катета к гипотенузе
|
| ||||||||||||||
| КОСИНУС Отношение прилежащего катета к гипотенузе |
| |||||||||||||||
| ТАНГЕНС Отношение противолежащего катета к прилежащему |
| |||||||||||||||
| КОТАНГЕНС Отношение прилежащего катета к противолежащему |
| |||||||||||||||
|
Свойства прямоугольного треугольника
| ||||||||||||||||
 А+ А+  В = 90 ̊
Сумма острых углов в прямоугольном треугольнике равна 90 ̊ В = 90 ̊
Сумма острых углов в прямоугольном треугольнике равна 90 ̊
|
Катет прямоугольного треугольника, лежащий против угла в |
а =
Если катет равен половине гипотенузы, то угол, лежащий против этого катета, равен 3 |
m =
Медиана, проведенная к гипотенузе, равна её половине и является радиусом описанной окружности
| |||||||||||||
|
Признаки равенства прямоугольных треугольников
| ||||||||||||||||
|
По гипотенузе и катету
а = |
По катету и прилежащему острому углу
|
По катету и противолежащему острому углу
|
| |||||||||||||
СООТНОШЕНИЯ МЕЖДУ ТРИГОНОМЕТРИЧЕСКИМИ ФУНКЦИЯМИ
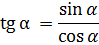
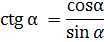
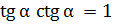
|
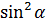 + + 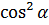 =1 – основное тригонометрическое тождество =1 – основное тригонометрическое тождество
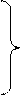
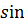 (90 ̊– α) = (90 ̊– α) = 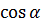
cos (90 ̊ – α) = cos (180 ̊– α) = –
|
ЗНАЧЕНИЯ СИНУСА, КОСИНУСА И ТАНГЕНСА НЕКОТОРЫХ УГЛОВ
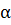
| 30 ̊ | 45 ̊ | 60 ̊ |
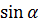
| 
| 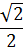
| 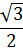
|
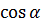
| 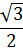
| 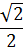
| 
|
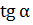
| 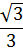
| 1 |
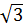
|
ЧЕТЫРЕХУГОЛЬНИКИ
АВСD - четырехугольник
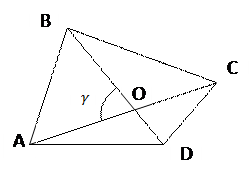 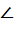 А + А + 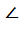 В + В + 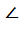 С + С + 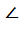 D = 360° D = 360°
|
S = 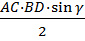 АС, ВD - диагонали
АС, ВD - диагонали
|
ПАРАЛЛЕЛОГРАММ
|
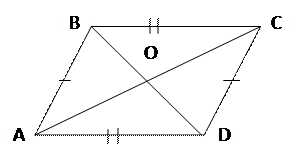
ABCD- параллелограмм
AB 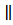 CD
BC CD
BC 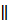 AD
Параллелограммом называется четырехугольник, у которого стороны попарно параллельны. AD
Параллелограммом называется четырехугольник, у которого стороны попарно параллельны.
|
СВОЙСТВА И ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА
 |
| Свойства параллелограмма | Признаки параллелограмма |
1) AB=CD; BC=AD
 A= A= 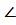 C; C;  B= B=  D
В параллелограмме противоположные стороны и противоположные углы равны
2) AC D
В параллелограмме противоположные стороны и противоположные углы равны
2) AC 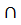 BD = O, AO = OC, BO = OD
Диагонали параллелограмма делятся точкой пересечения пополам.
3) BD = O, AO = OC, BO = OD
Диагонали параллелограмма делятся точкой пересечения пополам.
3)  А + А +  В = 1800
В параллелограмме сумма углов, прилежащих к одной стороне, равна 1800
4) В = 1800
В параллелограмме сумма углов, прилежащих к одной стороне, равна 1800
4) 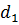 ² + ² + 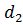 ² = a ² + b ² + c ² + d ²
где ² = a ² + b ² + c ² + d ²
где 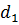 = AC ; = AC ; 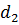 = BD – диагонали;
a = AD ; b = AB ; c = BC ;
d = CD – стороны
5) P = 2( a + b ) – периметр параллелограмма,
где a = AD; b = AB = BD – диагонали;
a = AD ; b = AB ; c = BC ;
d = CD – стороны
5) P = 2( a + b ) – периметр параллелограмма,
где a = AD; b = AB
| 1) (AB 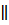 CD; AB = CD) CD; AB = CD)  (ABCD-параллелограмм)
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
2) (AB = CD; BC = AD) (ABCD-параллелограмм)
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
2) (AB = CD; BC = AD)  (ABCD-параллелограмм)
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм
3) (AO = OC; BO = OD,
где O = AC (ABCD-параллелограмм)
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм
3) (AO = OC; BO = OD,
где O = AC  BD) BD)  (ABCD-параллелограмм)
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм (ABCD-параллелограмм)
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм
|
ПЛОЩАДЬ ПАРАЛЛЕЛОГРАММА
| S = ah , где a = AD – основание h = BH – высота |
S = ab 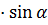 ,
где а = AD, b = AB, ,
где а = AD, b = AB,
 a = a = 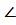 BAD BAD
|
S = 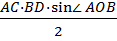
|
S= 4 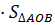
|
ЧАСТНЫЕ СЛУЧАИ ПАРАЛЛЕЛОГРАММА
| Вид | Свойства | Формулы |
ABCD – прямоугольник – это параллелограмм, у которого все углы прямые
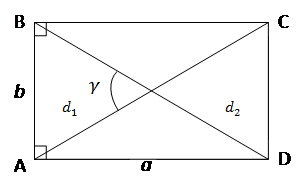  A = A = 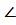 B = B = 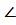 C= C= 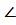 D = 90° D = 90°
|
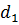 = = 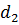 Диагонали прямоугольника равны.
Диагонали прямоугольника равны.
| S = 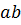 S =
S = 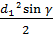 – площадь
P = 2(a + b) - периметр
d1² = a²+b²
где d 1 , d 2 – диагонали,
а, b – стороны прямоугольника – площадь
P = 2(a + b) - периметр
d1² = a²+b²
где d 1 , d 2 – диагонали,
а, b – стороны прямоугольника
|
ABCD – ромб – это параллелограмм,
у которого все стороны равны
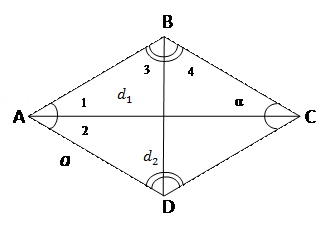 AB = BC = CD = AD AB = BC = CD = AD
|
 1= 1=  2, 2,  3= 3=  4, 4,
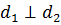 Диагонали ромба взаимно перпендикулярны и делят его углы пополам
Диагонали ромба взаимно перпендикулярны и делят его углы пополам
|
S = 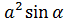 S =
S = 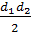 - площадь
Р = 4а – периметр - площадь
Р = 4а – периметр
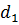 ² + ² + 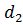 ² = 4 a ²
где d 1 , d 2 - диагонали,
а – сторона ромба, ² = 4 a ²
где d 1 , d 2 - диагонали,
а – сторона ромба,
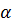 – угол ромба – угол ромба
|
ABCD – квадрат - это прямоугольник,
у которого все стороны равны
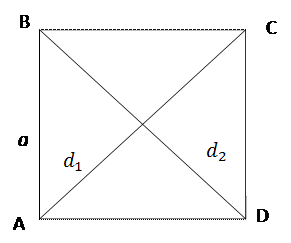 AB = BC = CD = AD AB = BC = CD = AD
|
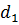 = = 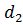
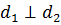 Диагонали квадрата равны,
взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Диагонали квадрата равны,
взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
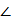 A= A= 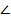 B= B= 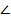 C= C= 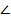 D =90° D =90°
| S = a²  – площадь
S = – площадь
S = 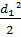 S=
S= 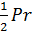 ,
где r – радиус вписанной окружности
Р = 4а - периметр ,
где r – радиус вписанной окружности
Р = 4а - периметр
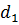 = а = а 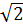 где d 1 , d 2 - диагонали, а – сторона квадрата
где d 1 , d 2 - диагонали, а – сторона квадрата
|
ТРАПЕЦИЯ
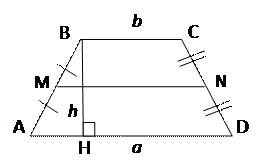
| ABCD - трапеция
AD = a, BC = b  – основания
AB, CD – боковые стороны
BH = h - высота
AD – основания
AB, CD – боковые стороны
BH = h - высота
AD  BC;
S = BC;
S = 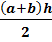 MN – средняя линия трапеции,
где М – середина АВ
N – середина СD
MN
MN – средняя линия трапеции,
где М – середина АВ
N – середина СD
MN  BC; MN BC; MN  AD; MN= AD; MN= 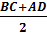 Средняя линия трапеции параллельна
основаниям и равна их полусумме.
Средняя линия трапеции параллельна
основаниям и равна их полусумме.
|
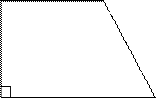
| Трапеция прямоугольная, если один из углов прямой |

| Трапеция равнобедренная, если ее боковые стороны равны |
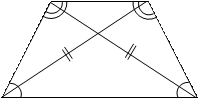
| В равнобедренной трапеции: 1) диагонали равны; 2) углы при основании равны; 3) середины сторон являются вершинами ромба. |

| Биссектрисы углов, прилежащих к боковой стороне, перпендикулярны |
ОКРУЖНОСТЬ
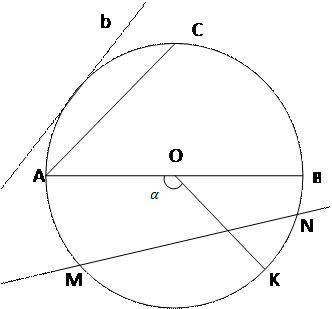
Окр. (О; r)
т. О – центр окружности
OK = OB = OA = r – радиус
AB = d – диаметр
b – касательная
AC – хорда
MN - секущая
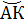 - дуга окружности
d = 2 r - дуга окружности
d = 2 r
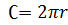 - длина окружности - длина окружности
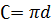 L
L 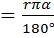 - длина дуги - длина дуги
| 
|
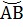 - дуга окружности - дуга окружности
 АОВ - центральный угол АОВ - центральный угол
 АОВ = АОВ = 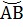 Градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
Градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
 АСВ – вписанный угол АСВ – вписанный угол
 АСВ = АСВ = 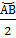 Вписанный угол измеряется половиной дуги, на которую опирается.
Вписанный угол измеряется половиной дуги, на которую опирается.
 АСВ = АСВ = 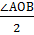 , если , если 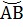 меньше полуокружности меньше полуокружности
| 
| |||
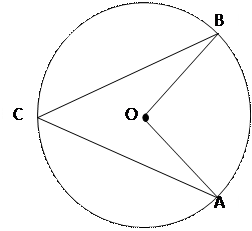
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
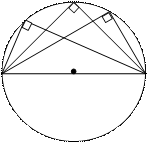
| Вписанный угол, опирающийся на полуокружность – прямой.
|
ПЛОЩАДЬ
Площадь круга
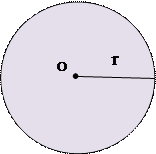
| 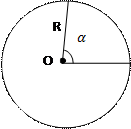 Площадь сектора Площадь сектора
|
S = 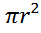
| S = 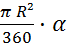
|
СВОЙСТВА ОКРУЖНОСТИ И ЕЁ ЭЛЕМЕНТОВ
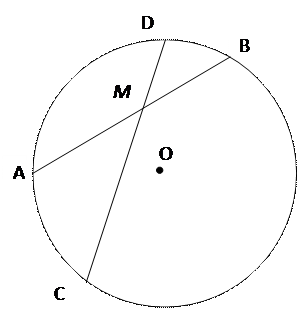
Свойство хорд
AB; CD – хорды
AB 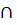 CD = M
AM · MB = CM · MD
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. CD = M
AM · MB = CM · MD
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
| 
|
Свойство касательной
ОМ – радиус
а – касательная
М – точка касания
ОМ 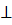 а
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. а
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
| 
|
| АТ – касательная АВ; АХ – секущие АТ² = АХ · АY АТ² = АВ · АС | 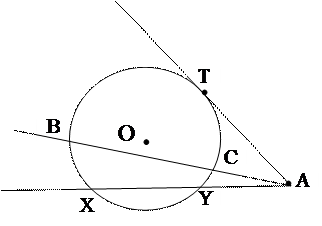
|
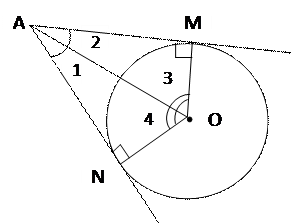
AM, AN – касательные
M, N – точки касания
AM = AN
 1 = 1 =  2; 2;  3 = 3 =  4
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. 4
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
| 
|












 ab <
ab < 
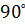

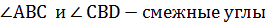
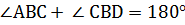
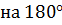 .
.
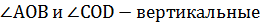
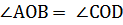

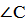 =60
=60 
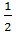 ah
ah 
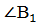
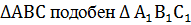
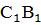 АС=
АС= 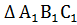

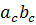
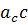
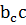
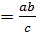
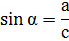
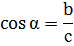
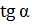 =
= 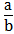
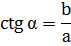
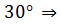 а =
а = 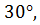 равен половине гипотенузы
равен половине гипотенузы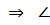 А =
А = 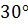
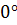
 c = R
c = R 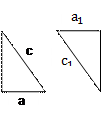
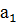 с =
с =