3 Частотні характеристики резонансного підсилювача
Схема простого резонансного підсилювача на транзисторі зі СЕ (рисунок 1,а) відрізняється від аперіодичного підсилювача тільки колом навантаження. В даному випадку навантаженням є резистор Rш, шунтуючий паралельний коливальний контур LC. Як правило, втратами потужності в котушці індуктивності L і конденсаторі C можна знехтувати порівняно з потужністю, що виділяється на резисторі Rш. При цій умові повна провідність навантаження (між зажимами 1-2)
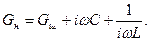(1)
Приведемо основні параметри контура LC з шунтом Rш:
резонансна частота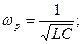 
характеристичний опір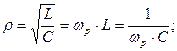 
затухання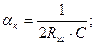 
постійна часу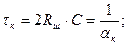 
добротність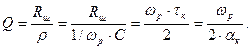 
Виходячи зі схеми заміщення підсилювача (рисунок 1, б) і спираючись на формулу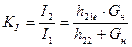 
(з заміною 
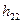на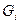 
), визначаємо передаточну функцію підсилювача.
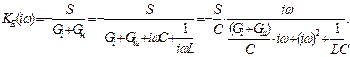(2)
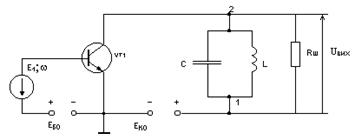
а)
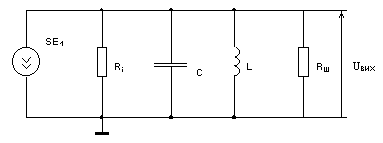
б)
Рисунок 1 – Резонансний підсилювач (а) і схема заміщення колекторного кола (б)
Складова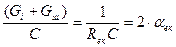 
в знаменнику виразу (2) враховує шунтуючий вплив активного елемента на затухання контура. З урахуванням приведених вище позначень параметрів контура передаточна функція (2) приводиться до виду
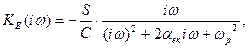(3)
або
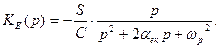(4)
Для високо добротних контурів основним параметром є значення передаточної функції підсилювача на частотах, близьких до резонансної частоти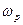 
. В цьому випадку вираз (3) можна привести до вигляду
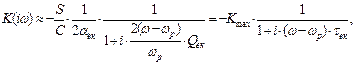(5)
де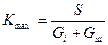 
- максимальне підсилення (на частоті 
); 
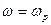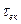- постійна часу контура з урахуванням впливу внутрішньої провідності активного елемента 
.
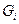Величину
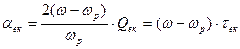(6)
часто називають загальною розстройкою контура.
Так, вираз (5) можна записати в формі
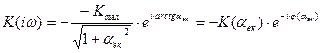. (7)
Характеристики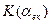 
і 
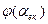резонансного підсилювача представлені на рис. 2.
Відносна смуга пропускання резонансного підсилювача, що визначається по ослабленню амплітуди на границях смуги до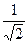 
від максимального рівня (при 
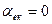) і виразу через загальну розстройку 
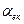, дорівнює 2 (див. рис. 2).
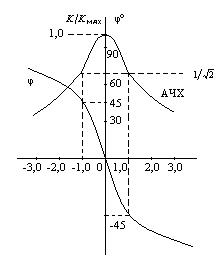
Рисунок 2 – Амплітудно-частотна і фазо-частотна характеристики одноконтурного резонансного підсилювача
Для переходу від безрозмірної відносної смуги пропускання 2 до розмірної смуги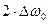 
, підставимо в (6) 
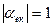, а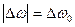 
.
Тоді
,
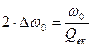де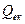 
, як це слідує з (6), добротність напруженого контура.
Як заключення приведемо спрощений вираз для імпульсної характеристики резонансного підсилювача
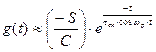(8)
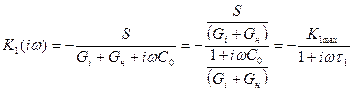,(9)
Порівняння виразів (7) і (9) вказує на те, що передаточну функцію резонансного підсилювача можна отримати за рахунок зсуву передаточної функції відповідного аперіодичного підсилювача по вісі частот на величину 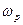. Треба лише постійну часу 
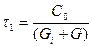прирівняти до величини 
.
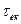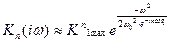, (10)
Все сказане можна поширити також на каскадне з’єднання ідентичних резонансних підсилювачів. Приведена формула (10) дозволяє відразу написати аналогічний вираз для передаточної функції резонансного n- каскадного підсилювача (фільтра)
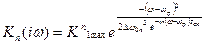, (11)
де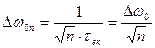 
, а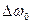 
- півширина смуги пропускання одного каскаду.
Передаточна функція резонансного підсилюваа з навантаженням у вигляді магнітно-зв’язаних контурів визначається наступним чином:
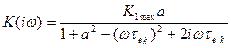, (12)
де a – коефіцієнт магнітного зв’язку.
Відповідно, амплітудно - частотну та фазо - частотну характеристики такого підсилювача зображено на рис.3. Щільна лінія відповідає настроєному режиму підсилювача, пунктир – розстроєному режиму на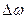 
.
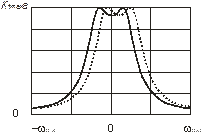
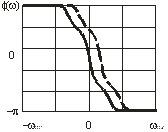
а) б)
Рисунок 3 - Амплітудно-частотна (а) і фазо-частотна (б) характеристики одноконтурного резонансного підсилювача з навантаженням у вигляді магнітно-зв’язаних контурів