2 метод інтеграла накладення
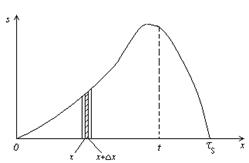
Замість розкладення складного сигналу на гармонійні складові (спектральний метод) можна застосувати розбиття сигналу на достатньо короткі імпульси (рис. 2).
Якщо в основі спектрального методу лежить передаточна функція кола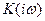 
, то метод інтеграла накладення оснований на імпульсній характеристиці кола 
.
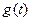Нехай треба знайти сигнал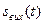 
на виході кола, якщо задано сигнал 
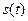на вході кола та відома її імпульсна характеристика 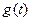. Для розуміння суті метода інтеграла накладення зробимо наступне. Розіб’ємо довільний сигнал 
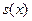на елементарні імпульси, як це показано на рисунку 2,а, та знайдемо відгук кола в момент 
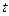на елементарний імпульс (на рис.2,а заштриховано), що діє на вході в момент 
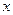. Якби площа цього імпульса дорівнювала одиниці, то імпульс можна було б розглядати як дельта-функцію, що виникла в момент 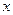.при імпульсній характеристиці кола 
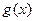відгук в момент 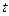був би рівним 
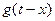. Оскільки заштрихована на рис. 2,а площа імпульса дорівнює 
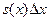(а не одиниці), відгук в момент 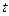буде 
.
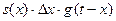Для визначення повного значення вихідного сигналу в момент 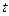треба просумувати дію всіх імпульсів на проміжку від 
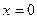до 
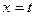. При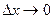 
сумування зводиться до інтегрування.
Отже,
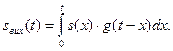(9)
В загальному випадку, якщо початок сигналу 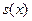не співпадає з початком відліку часу 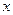, останній вираз можна записати у формі
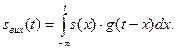(10)
Для реальних кіл завжди виконується умова
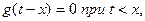(11)
тобто, при від’ємному аргументі функція 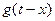повинна перетворюватися на нуль, так як відгук не може випереджати вплив. Тому вираз (9) можна замінити виразом
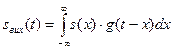(12)
(при цьому мається на увазі, що для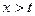 
підінтегральний вираз перетворюється на нуль).
а)
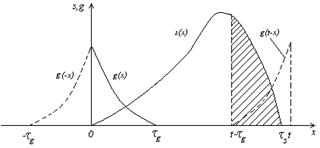
б)
Рисунок 2. Розбиття сигналу на короткі імпульси (а) і згортка сигналу з імпульсною характеристикою (б)
Приведемо, нарешті, ще одну форму запису, яку отримуємо з виразу (9) при заміні 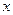на 
:
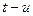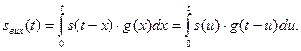(13)
Інтеграл, який знаходиться в правій частині виразу (9), в математиці називається згорткою функцій 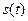і 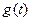. Таким чином, приходимо до наступного важливого положення: сигнал 
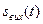на виході лінійного кола є згорткою вхідного сигналу 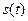з імпульсною характеристикою кола .
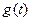З виразу (9) видно, що сигнал на виході кола 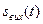в момент 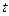отримуємо сумуванням миттєвих значень вхідного сигналу 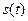, які беруться з вагою 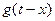за весь попередній час.
При сумуванні спектра вхідного сигнала ваговою функцією була передаточна функція кола 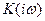. В даному випадку при сумуванні миттєвих значень вхідного сигналу 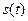ваговою функцією є імпульсна характеристика кола, взята з аргументом 
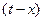, тобто функція .
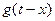З рисунка 2,б, побудованого для моменту часу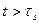 
, видно, що відгук кола на вплив 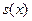не може закінчитися раніше, ніж функція 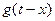зміститься вправо від 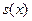на час, рівний довжині імпульсної характеристики 
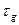. Іншими словами, сигнал на виході кола не може бути коротшим 
.
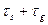Для того, щоб при проходженні через коло сигнал не подовжувався, треба виконувати умову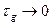 
, тобто імпульсна характеристика кола повинна наближатися до дельта-функції, а це рівнозначно умовам рівномірності передаточної функції 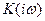при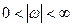 
.