1 спектральний метод
В основі цього методу лежить використання введеної в попередньому розділі передаточної функції кола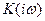 
. Якщо на вході лінійного чотириполюсника діє сигнал довільної форми у вигляді ЕРС 
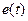, то, використовуючи спектральний метод, треба визначити спектральну щільність вхідного сигналу 
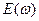. Ця операція легко виконується за допомогою наступного виразу (1)
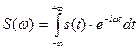. (1)
Множенням 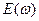на 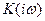визначається спектральна щільність сигналу на виході чотириполюсника. Нарешті, застосування до множення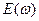 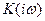оберненого перетворення Фур’є визначає вихідний сигнал у вигляді функції часу.
Таким чином, якщо вхідний сигнал записаний у вигляді інтегралу:
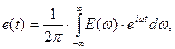(2)
то вихідний сигнал можна подати в аналогічній формі
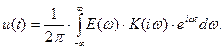(3)
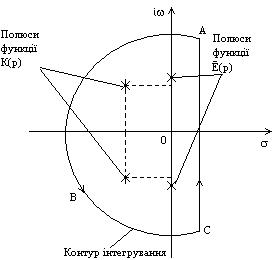
Рисунок -1 Контур інтегрування при t >0
Порівняння виразу (3) з (2) показує, що сигнал на виході лінійного кола можна отримати додаванням складових спектру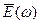 
вхідного сигналу, взятих з урахуванням 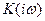. Іншими словами, передаточна функція кола 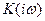є вагомою функцією, що визначає відносний вклад різних складових спектру 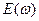в сигнал 
.
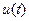Відмічалось, що аналіз перехідних процесів значно спрощується при представленні як зовнішньої дії, так і передаточної функції у вигляді перетворень Лапласа. При цьому позначення передаточної функції можна зберегти попереднім, а змінити лише аргумент, так що 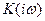перейде в 
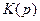. Функція 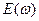переходить в 
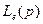. Перетворення Лапласа від функції часу 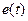в подальшому позначається символом 
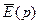. При цьому вираз (3) приводиться до вигляду
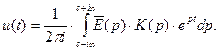(4)
При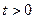 
замкнений контур інтегрування, створений додаванням дуги безкінечно великого радіусу в лівій півплощині (рис. 1),охоплює всі полюси підінтегральних функцій як 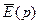, так і 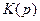, завдяки чому має місце співвідношення
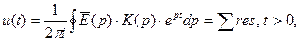(5)
(тут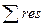 
- сума лишків/відрахувань(вычетов) в указаних полюсах).
При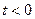 
контур інтегрування лежить в правій півплощині, не має полюсів та інтеграл дорівнює нулю.
Показане на рисунку 1 розміщення полюсів функції 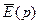(на уявній осі) відповідає ЕРС виду 
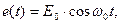що існує при 
.
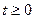Тому обчислення інтеграла (5) зводиться до визначення лишків/відрахувань у полюсах підінтегральної функції. Подамо підінтегральну функцію виразу (5) у вигляді
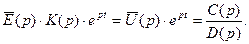(6)
В даному випадку знаменник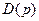 
знаходиться множенням множників виду 
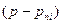, де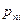 
- полюси не тільки функції 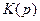, але і функції .
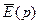Тоді лишок/відрахування функції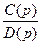 
, що має в точці 
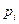простий полюс (першої кратності), визначається за формулою
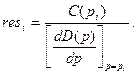(7)
Якщо функція 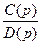має в точці 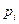полюс кратності 
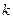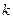( - ціле додатнє число), то
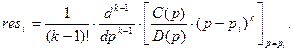(8)
Методика використання контурних інтегралів для визначення деяких функцій, що грають велику роль в теорії перехідних процесів, в подальшому буде пояснена на прикладах.