СИГНАЛИ та процеси в радіотехніці
Міністерство освіти І науки України
Запорізький національний технічний університет
Методичні вказівки
до лабораторних робіт з дисципліни
СИГНАЛИ та процеси в радіотехніці
Частина 2
для студентів спеціальності 7.090.701
“Радіотехніка”
всіх форм навчання
2010
Методичні вказівки до лабораторних робіт з дисципліни „Сигнали та процеси в радіотехніці для студентів спеціальності 7.090701 всіх форм навчання. Частина 2./Укл. Т.І. Бугрова. – Запоріжжя: ЗНТУ, 2010. - 27 с.
Укладач: Т.І. Бугрова, ст. викладач
Рецензент: М.М. Касьян, к.т.н., доцент
Відповідальний за випуск: Т.І. Бугрова, ст. викладач
Затверджено на засіданні кафедри
„Радіотехніки і телекомунікацій”
Протокол №11 від 27 квітня 2009р.
ЗМІСТ
1 ЛАБОРАТОРНА РОБОТА № 5 . ВІДНОВЛЕННЯ СИГНАЛІВ
ЗА ДИСКРЕТНИМИ ВІДЛІКАМИ КОТЕЛЬНИКОВА 4
2 ЛАБОРАТОРНА РОБОТА № 6.ПРОХОДЖЕННЯ РАДІОІМПУЛЬСІВ КРІЗЬ ВИБОРЧІ КОЛА 1 2
3 ЛАБОРАТОРНА РОБОТА № 7 ПРОХОДЖЕННЯ АМ-КОЛИВАНЬ КРІЗЬ ВИБОРЧІ КОЛА 20
ПЕРЕЛІК ПОСИЛАНЬ 27
5 Лабораторна робота № 5.
ВІДНОВЛЕННЯ СИГНАЛІВ ЗА ДИСКРЕТНИМИ
ВІДЛІКАМИ КОТЕЛЬНИКОВА
Мета роботи – вивчення можливості синтезу сигналів по дискретним відлікам у відповідності до теореми Котельникова, дослідження впливу частоти вибірки та характеристик фільтрів нижніх частот на якість синтезу.
5.1 Основні позначення, розрахункові формули та визначення
Відповідно до теореми Котельникова сигнал s(t), який не складається з частот вище Fm, повністю визначається своїми миттєвими значеннями s(n∆t), відлік яких йде через інтервал часу ∆t=1/2 Fm:
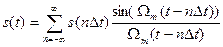 (5.1)
(5.1)
Відліки сигналу s(t) у моменти часу n∆t є коефіцієнтами Фур’є Сn=s(n∆t) розкладання сигналу s(t) по ортогональній системі функцій відліку:
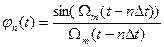 .
.
Спектральне пояснення теореми Котельникова дає рис.5.1, на якому зображені вихідний сигнал s(t) (рис. 5.1,a), його спектр S(ω) (рис. 5.1, д), та вибіркові сигнали
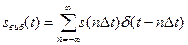 (5.2)
(5.2)
і їх спектри
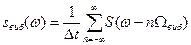 (5.3)
(5.3)
для різних частот вибірок Ωвиб=2πF виб =2π/∆t.
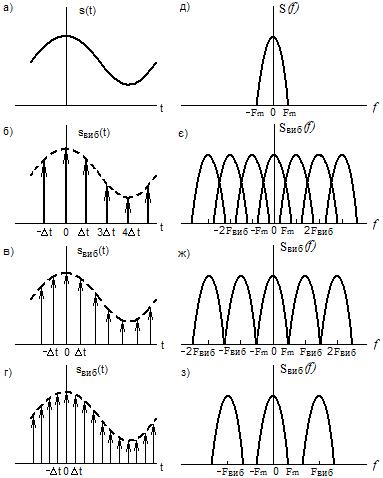
Рисунок 5.1- Сигнали та їх спектри (до спектрального
пояснення теореми Котельникова):
а – сигнал s(t); б – вибірковий сигнал sвиб(t) при Fвиб<2Fm;
в – sвиб(t) при Fвиб=2Fm; г – sвиб(t) при Fвиб>2Fm;
д – спектр S(f) сигналу s(t); є – спектр вибірного сигналу
Sвиб(f) при Fвиб<2Fm; ж – Sвиб(f) при Fвиб=2Fm;
з – Sвиб(f) при Fвиб>2Fm.
Спектром вибіркового сигналу є сума копій спектра сигналу s(t) з центральними частотами 0; ±2Ωвиб, тощо. Якщо ∆t≤1/2 Fm, Ωвиб >2Ωm, тоді можливо відтворення вихідний сигнал s(t), пропустивши вибірковий сигнал (5.2) через ідеальний фільтр нижніх частот (ФНЧ) з комплексним коефіцієнтом передачі
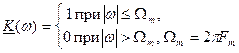 (5.4)
(5.4)
Імпульсна характеристика такого фільтру з точністю до постійного множника співпадає з функцією відліків φ0(t):
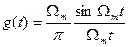 (5.5)
(5.5)
Якщо ж ∆t>1/2Fm, Ωвиб <2Ωm, тоді сусідні копії спектру перекриваються і відтворення сигналу s(t) неможливе. Мінімальний інтервал (період) вибірки дорівнює ∆t=1/2Fm, що і стверджується у теоремі Котельникова.
При практичному використанні теореми Котельникова для відтворення сигналів по відлікам необхідно урахувати похибки.
Причини для цього наступні:
1. Сигнали з обмеженим спектром нескінченні у часі, тому відтворення миттєвого значення s(t) принципово потребує урахування нескінченної множини дискретних відліків. Використання відліків, узятих в обмеженому інтервалі (0, T), означає перехід до кінцевої межі (0, 2FmT) в ряду (5.1) і викликає появу помилки відтворення.
2. Сигнали кінцевої довжини мають нескінченні частотні спектри. В даному випадку Ωm звичайно вибирають так, щоб у діапазоні частот від нуля до Ωm була зосереджена завдана частина енергії сигналу. Зрозуміло, що похибка відтворення тим більше, чим „повільніше” спадає спектр сигналу за межею вибраної смуги від 0 до Ωm.
3. Відхилення характеристик реальних фільтрів нижніх частот від ідеальних (5.4) та (5.5) призводить до появи додаткових похибок відтворення сигналу s(t) по відлікам Котельникова.
5.2 Опис лабораторної установи
У змінному пристрої знаходиться матричний генератор 20 відлікових імпульсів, потенціометри встановлення полярності та амплітуд відлікових імпульсів, суматор, два фільтра нижніх частот з граничними частотами 5 кГц, тумблер „Синтез” – „Вимірювання частотної характеристики фільтру”, тумблер „фільтр НЧ-1” – „фільтр НЧ-2” і схема, що генерує імпульс синхронізації.
Вигляд передньої панелі функціонального пристрою показаний на рис. 5.2. Запуск генератора відлікових імпульсів здійснюється синусоїдальним сигналом зовнішнього лабораторного генератора, який підключається до розніму Г1; при цьому частота проходження відлікових імпульсів (частота вибірок Fвиб) дорівнює частоті зовнішнього генератора, а часовий інтервал між відліковими імпульсами ∆t=1/ Fвиб.
Цей же зовнішній генератор використовується для виміру частотних характеристик фільтрів НЧ; у цьому випадку він повинен бути підключений до гнізда Г2.
Сигнал з виходу ФНЧ (першого або другого залежно від положення відповідного тумблера) надходить на гнізда Г3. Сигнал, що діє на вході фільтрів (вибірковий при синтезі й синусоїдальний при вимірі частотних характеристик), надходить на гнізда Г4. До гнізда Г5 подається імпульсний сигнал для зовнішньої синхронізації осцилографа.
5.3 Домашнє завдання
1. Зобразити сигнали, синтезовані в лабораторній роботі: а) відеоімпульси прямокутної форми тривалістю 0,2; 0,4; 0,6 мс; б) симетричний відеоімпульс трикутної форми тривалістю 0,4 мс; в) радіоімпульси прямокутної форми тривалістю 0,4; 0,8 мс і частотою заповнення f0=2,5 кГц; г) фазо-маніпульований радіосигнал тривалістю 2 мс із частотою заповнення f0=2,5 кГц і зміною фази на p після кожного періоду заповнення; д) радіоімпульс із прямокутної огинаючої й лінійною зміною частоти заповнення від 0 до 5 кГц.
2. Розрахувати й побудувати ідеальні вибіркові сигнали для сигналів, зазначених у п. 1а, 1б, 1в при Fвиб=5,10,20 кГц, для сигналів (див. п. 1г й 1д) при Fвиб=10кГц.
У додатку 3 наведений розрахунок вибіркового сигналу для радіоімпульсу з лінійною частотою модуляції (для сигналу, зазначеного в п. 1д) за допомогою мікрокалькулятора В3-34.
3. Побудувати спектр синтезованих сигналів (див. п. 1а, 1б, 1в) і відповідних їм вибіркових сигналів по формулі (5.3), обчисливши точно лише частоти, що відповідають нульовим значенням спектральної щільності.
4. Розрахувати й побудувати частотні характеристики ідеального ФНЧ із граничною частотою Fт=5 кГц.
5.4 Лабораторне завдання й методичні вказівки
1. Зняти амплітудно-частотні K(f) і фазо-частотні характеристики φ(f) LC- і RC-фільтрів нижніх частот 1 й 2 у діапазоні частот 200 Гц–10 кГц при Uвх=1 У. Визначити граничні частоти фільтра на рівні 0,5.
1.1 Підготувати лабораторний генератор, вольтметр, осцилограф і лабораторну установку до роботи. Установити вихідний опір лабораторного генератора рівним 5 Ом, вихідну напругу - 1 В, включити внутрішнє навантаження генератора. Тумблер «Синтез - Вимір частотних характеристик фільтру» поставити в положення «Вимір частотних характеристик фільтру».
1.2 Зібрати схему дослідження. Підключити генератор до гнізда Г2 лабораторні установки, входи «Y» й «X» осцилографа приєднати до гнізд Г3 і Г4, вольтметр підключити до вхідних клем підсилювача вертикального відхилення осцилографа. Виключити розгорнення осцилографа.
1.3 зняти залежність K(f) і φ(f). Установити частоти 200 Гц, 1, 2, 3, ..., 10 кГц.
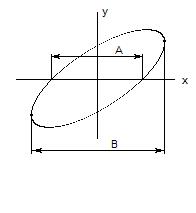
Для кожного значення частоти фіксувати по вольтметрі значення Uвих, а по фігурі Лісажу на екрані осцилографа (рис. 5.3) – значення А и В.
Фазове зрушення між напругами на вході й виході фільтра
φ=arcsin A/B (5.6)
Тому що Uвх=1 У, та вихідна напруга фільтра, вимірювана вольтметром, чисельно дорівнює модулю коефіцієнта передачі фільтра.
|
Рекомендується вимір частотних характеристик фільтрів НЧ-1 і НЧ-2 робити одночасно.
2. Одержати й замалювати осцилограми імпульсних характеристик фільтрів НЧ-1 і НЧ-2.
2.1 Зібрати схему дослідження.
Підключити лабораторний генератор до гнізда Г1, установити вихідну напругу генератора Uвих=2÷3 В і частоту Fвиб=10 кГц.
Тумблер «Синтез - Вимір частотних характеристик фільтра» поставити в положення «Синтез».
Вхід підсилювача вертикального відхилення осцилографа підключити до гнізда Г4. Для зовнішньої синхронізації осцилографа використати імпульси, що знімають із гнізда Г5.
2.2 Встановити масштаб горизонтальної розгортки 20 мкс/мм. Одержати на екрані осцилографа стійку осцилограму 20 вибіркових імпульсів. Відрегулювати підсилення каналу X осцилографа так, щоб інтервалу між сусідніми вибірками ∆t=1/Fвиб=100 мкс на екрані осцилографа відповідала відстань 5 мм по осі x .
2.3 Установити максимальну амплітуду першого відлікового імпульсу позитивної полярності, а амплітуди інших імпульсів рівними нулю. Помітити положення на екрані першого відлікового імпульсу.
2.4 Підключити вхід підсилювача Y-каналу осцилографа до гнізда Г3, посилення Y-каналу збільшити в десять разів. Спостерігати імпульсні характеристики фільтрів, звернувши увагу на часові зміщення осцилограм щодо початку імпульсу, який діє на входах ФНЧ. Замалювати осцилограми.
3. Синтезувати сигнали, перераховані в домашньому завданні. Замалювати осцилограми всіх вибіркових (гніздо Г4) і синтезованих сигналів (гніздо Г3) на вході фільтрів НЧ-1 і НЧ-2.
3.1 У всіх випадках, регулюючи посилення X-каналу, підтримувати масштаб горизонтальної розгортки однаковим і рівним 20 мкс/мм.
3.2 Установити розраховані значення амплітуд відлікових імпульсів на осцилографі, підключивши Y-канал осцилографа до входу фільтра – до гнізда Г4.
3.3 Підключити осцилограф до гнізда Г3. Спостерігати синтезовані сигнали на вході ФНЧ-1 і ФНЧ-2. Замалювати осцилограми, звертаючи увагу на часові зміщення синтезованих сигналів щодо вибіркових.
5.5 Вказівки до звіту
Звіт повинен містити:
1) функціональну схему пристрою для синтезу сигналів по дискретним відлікам Котельникова;
2) частотні й імпульсні характеристики ФНЧ-1 і ФНЧ-2 й ідеального ФНЧ;
3) графіки всіх вибіркових сигналів;
4) осцилограми всіх вибіркових і синтезованих сигналів в однаковому часовому масштабі;
5) спектри вибіркових сигналів;
6) висновки й оцінку отриманих результатів.
5.6 Контрольні запитання
1. Сформулюйте теорему Котельникова для сигналів з обмеженим спектром.
2. Який вид має спектр дискретного вибіркового сигналу?
3. Запишіть ряд Котельникова по ортогональних функціях відліку. Чому дорівнюють коефіцієнти цього ряду?
4. Дайте спектральне пояснення теореми Котельникова.
5. Для чого при відновленні вибіркового сигналу застосовується ідеальний ФНЧ?
6. Отримайте вираз для імпульсної характеристики ідеального ФНЧ. Змалюйте графік.
7. Який вид мають амплітудно-частотна й фазо-частотна характеристики ідеального ФНЧ?
8. Поясніть похибки синтезування реальних сигналів по дискретним відлікам.
9. Як залежить похибка відновлення сигналу, пов'язана з обмеженістю меж підсумовування, від часу?
10. Покажіть, як виражається енергія й середня потужність через послідовність часових вибірок.
11. Обмежуючи спектр відеоімпульсу прямокутної форми тривалістю 0,2; 0,4; 0,6 мс першим нулем спектральної щільності, визначте частоту вибірок, що відповідає теоремі Котельникова, і порівняйте із частотою Fвиб = 5, 10 й 20 кГц, прийнятою в лабораторному завданні.
12. Зобразіть декілька перших складових ряду Котельникова, що апроксимує відеоімпульс прямокутної форми тривалістю 0,2 мс при ∆t1=1/4Fm, ∆t2=1/2Fm, ∆t3=1/Fm. Зауважте, що Fm – частота першого нуля спектральної щільності сигналу.
13. Зобразіть вибіркові сигнали і їхні спектри для відеоімпульсу прямокутної форми тривалістю 0,2; 0,4; 0,6 мс при умовах і допущеннях, прийнятих у п. 11.
14. Дайте відповіді на п. 11, 12, 13 для відеоімпульсу симетричної трикутної форми.
15. Вибірки з гармонічного коливання із частотою f0=0,45Fвиб подаються на реальний ФНЧ із граничною частотою Fm=0,5Fвиб. Що являє собою сигнал на виході фільтра?
16. Вибірки із сигналу з обмеженим спектром, узяті по теоремі Котельникова, подаються на ідеальний смуговий фільтр зі смугою прозорості від f1=3Fm до f2=5Fm. Що являє собою сигнал на виході фільтра?
17. Використовуючи властивості взаємної замінності змінних t й w у перетвореннях Фур'є, сформулюйте теорему, зворотну теоремі Котельникова, для сигналів, обмежених у часі. Поясніть теорему за допомогою графіків спектрів і сигналів, аналогічних графікам, наведеним на рис. 5.1.
6 Лабораторна робота № 6.








