Ряд (2.2) описує періодичний сигнал s ( t ) у вигляді суми постійної складової та гармонійних складових з амплітудами А n і початковими фазами .

Дата: 2025-05-01; Просмотры: 4
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Сукупність амплітуд, фаз і частот гармонійних складових називають спектром амплітуд, спектром фаз і спектром частот. Амплітудно-частотний і фазо-частотний спектри можна уявити графічно.

Для періодичної послідовності прямокутних імпульсів з вишиною Е і протяжністю 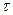та частотою 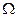амплітуди гармонійних складових визначаються виразом:

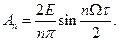(2.5)

 

Опис лабораторної установки

Лабораторний стенд складається із генератора імпульсів прямокутної форми, осцилографа та аналізатора спектра.

Принцип роботи аналізатора спектра оснований на явищі резонансу у високодобротному контурі. Якщо на вхід такого контура подати періодичний сигнал, у якого одна із гармонік спектру має частоту, що співпадає із резонансною частотою контура, то на виході контура практично виділяється тільки ця гармоніка. При цьому виділення гармоніки тим краще, чим вужча смуга пропускання контура в порівнянні з частотним інтервалом між сусідніми гармоніками сигналу, який аналізується.

Генератор прямокутних імпульсів генерує такі імпульси, частоти і тривалості яких можна змінювати за допомогою ручок керування на лицьовій панелі генератора.

Для гармонійного аналізу сигналу необхідно з виходу генератора прямокутних імпульсів подати сигнал на вхід осцилографа і замалювати форму імпульса. Для отримання кращої якості осцилограм синхроімпульс з генератора прямокутних імпульсів подається на синхровхід осцилографа, при цьому режим синхронізації осцилографа переключається на зовнішню синхронізацію.

Для отримання амплітудного спектру сигналу послідовність прямокутних відеоімпульсів з виходу генератора подається на вхід аналізатора спектра, після чого на екрані аналізатора з’являється спектр.

Розрахункове завдання

 

1 Розрахувати і побудувати амплітудно-частотний спектр періодичної послідовності прямокутних відеоімпульсів для наступних випадків:

1)

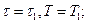
2)

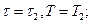
3)

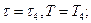
4)

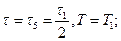
2 Розрахувати відносну та абсолютну похибки для апроксимації послідовностей з попереднього пункту десятьма та двадцятьма першими гармоніками ряду Фур’є.

3 Зібрати схему синтезатора та аналізатора сигналів по Фур’є у програмному середовищі Electronics Work Bench і одержати спектри сигналів та самі сигнали з пункту 1.

 

Лабораторне завдання

 

1. Одержати прямокутні уніполярні імпульси з параметрами із розрахункового завдання від генератора імпульсів, вімірити тривалість та період слідування їх за допомогою осцилографа. Замалювати осцилограми.

2. Одержати для всіх попередньо розрахованих сигналів амплітудні спектри, подаючи імпульси з виходу генератора на вхід аналізатора спектру. Замалювати спектри та визначити іх параметри.

Вимоги до звіту

 

Звіт повинен вміщувати в собі:

1. Розрахункові завдання.

2. Результати експериментальних вимірювань амплітудних спектрів сигналів.

3. Результати моделювання синтезатора досліджуваних сигналів в середовищі Work Bench.

4. Висновки з оцінкою результатів розрахунку, експериментів та моделювання.

 

Контрольні запитання

 

1. Властивості спектрів періодичних сигналів.

2. Вплив на спектр періодичної послідовності прямокутних відеоімпульсів змінення протяжності та періода повторення.

3. Як впливає на спектр періодичного сигналу зміна положення початку відліку часу?

4. Побудуйте і порівняйте спектри періодичної послідовності уніполярних та біполярних імпульсів.

5. Як зміниться спектр періодичного сигналу, якщо період його спрямувати до нескінченності?

6. Який зв’язок існує між суцільним спектром неперіодичного сигналу і лінійчатим спектром відповідного періодичного сигналу?

7. Запишіть вираз для спектральної щільності періодичного сигналу.

8. Запишіть спектр пачки із двох, трьох, п’яти і т. д. прямокутних відеоімпульсів.

9. Порівняйте спектри періодичної послідовності відеоімпульсів та пачки із декількох цих же імпульсів.

10. Як пов’язані між собою тривалість імпульса і ширина спектру?

3 ЛАБОРАТОРНА РОБОТА №3. АНАЛІЗ І СИНТЕЗ ЛІНІЙНИХ ЦИФРОВИХ ФІЛЬТРІВ

Ціль роботи – дослідити функціонування лінійних цифрових фільтрів, засвоїти навички їх синтезу та аналізу методами різницевих рівнянь, дискретної згортки, z-перетворень.

 

Короткі теоретичні відомості

 

Аналоговими називають сигнали, що представляють собою безупинні функції часу.

Відповідно, коло з RLC- елементів, керованих джерел струму і напруги (роль яких наприклад, можуть грати діоди, транзистори, операційні підсилювачі) будемо називати аналоговими.

Математичними моделями аналогових к i л є - диф. рівняння, КЧХ, передатні функції.

З метою підвищення якості обробки сигналів і використання для цих цілей спеціалізованих чи мікропроцесорів просто програми універсальних ЕОМ аналогові сигнали заміняються їхніми дискретними уявленнями - числовими послідовностями. Для повного відновлення сигналу його необхідно дискретизовать за часом з інтервалом Δt<=π/ωmax , де ωmax – максимальна частота в спектрі безупинного сигналу.

Позначимо дискретні отсчёты безупинного сигналу x(nΔt)=x(n).

Дискретним колом назвемо коло, що перетворить послідовність вхідних сигналів x(n) у послідовність y(n).

Аргумент n при цьому називається дискретним часом.

     
 


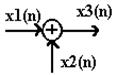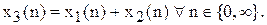Суматором послідовностей назвемо коло, що виконує математичну операцію підсумовування:

 

 

     
 


Перемножником на постійний коефіцієнт будемо називати коло, яке реалізуе функцію:

 


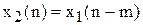Елементом затримки на число інтервалів часу m будемо називати коло із властивостями:

 

 


 

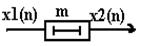Лінійними цифровими фільтрами (ЛЦФ) будемо називати кола, що складаються із сумматорів, перемножників, елементів затримки (елементів, що здійснюють лінійні операції над вхідними сигналами дискретного типу).

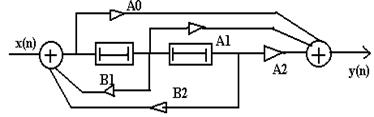
Приклад ЛЦФ та алгоритм його роботи.

 

Подамо сигнал x(n) на вхід ЛЦФ зі схемою:

 

     
 


 

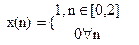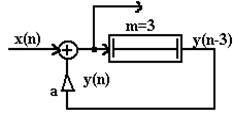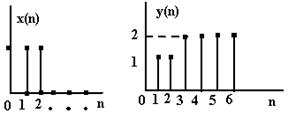
Виразимо математично вихідний сигнал y(n): y(n)=x(n)+ay(n-3) (3.1)

Рівняння (3.1)- називається різницевим рівнянням першого порядку,є повною математичною моделлю ЛЦФ, що дозволяє по вхідній послідовності x(n) розрахувати вихідну і навпаки. Нехай a=2, y(0)=0. Для всіх n<0


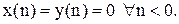
Тоді вихідна послідовність y(n):

 

n 0 1 2 3 4 5 6
x(n) 1 1 1 0 0 0 0
y(n) 1 1 1 2 2 2 2

 

Графіки вхідної і вихідної послідовностей

 


Математичною моделлю ЛЦФ N-го порядку в загальному випадку є різницеве рівняння N-го порядку виду:


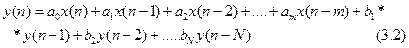
де M<=N, ai, bi- дійсні коефіцієнти.

Для перебування вихідної послідовності ЛЦФ y(n) необхідно знати вхідну послідовність x(n) і початкові умови y(-1),…..., y(-N).

( Це не значення вихідного сигналу, а саме початкові умови).

Класифікація ЛЦФ ґрунтується на обліку інформації про минулі стани системи.

Один із прикладів схемної реалізації зображений на рисунку:

 


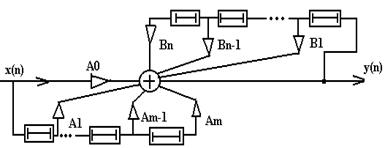Він зветься рекурсивний фільтр- від назви математичної операції- рекурсія-, що складається в циклічному звертанні до даних, отриманим на попередніх кроках.

Інший варіант ЛЦФ- трансверсальный фільтр (англ. “transverse”)- вхідні сигнали з затримкою і посиленням складаються в суматорi, щоб утворити вихідний сигнал.

 


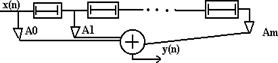Різницеве рівняння трансверсального фільтра:

y(n)=a0x(n)+a1x(n-1)+a2x(n-2)+…+amx(n-m) (3.3)

a0, a1,…,am-дійсні коефіцієнти.

m- порядок трансверсального фільтра.

Функція його - зважене підсумовування попередніх отсчётов вхідного сигналу, не використовуючи минулі в i дл i ки вхідного сигналу.

Фізично елемент затримки реалізується у виді регістра зрушення, перемножники – підсилювачем.

Рекурсивний фільтр має недолік – громіздку схему чи реалізацію, у випадку програмної реалізації вимагає великого обсягу пам'яті для збереження інформації окремо для рекурсивної і нерекурсивної частини. Більш досконалі - канонічні схеми рекурсивних цифрових фільтрів, у яких використовується мінімальна кількість елементів пам'яті P=max{N,M}.

 


Приклад: Схема рекурсивного фільтра 2-го порядку.

 

Методи аналізу ЛЦФ аналогічні методам аналізу лінійних аналогових кiл і є їх дискретними аналогами:

1) рішення різницевих рівнянь (аналог диф. рівнянь)

2) згортка з імпульсною характеристикою (аналог інтеграла накладення)

1) Z- перетворення (дискретний аналог перетворень Лапласа).

АНАЛІЗ ЛЦФ МЕТОДОМ РІШЕННЯ РІЗНИЦЕВИХ РІВНЯНЬ

полягає в простій підстановці вхідного сигналу в різницеве рівняння як повну модель ЛЦФ у прямому обчисленні по програмі (у випадку фільтрів великих порядків) вихідної послідовності.


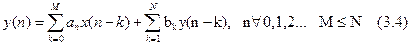
Приклад: нехай y(n)=x(n)-5y(n-1); початкові умови: y(-1)=0, x(n)=n+1

Пряма підстановка дає:

y(0)=x(0)-5y(-1)=1-5*0=1

y(1)=x(1)-5y(0)=2-5*1=-3

y(2)=x(2)-5y(1)=3-5*(-3)=18

y(3)=x(3)-5y(2)=4-5*18=-86

y(4)=x(4)-5y(3)=5-5*(-86)=475

Одержимо аналітичне рішення з різницею рівняння в явному виді. За аналогією з диф. рівнянням воно так само складається з загального і частккового рішень (із правою частиною - однорідного рівняння).

y(n)-5y(n-1)=0- однорідне рівняння. Рішення рівняння – вираження виду:


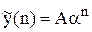
(за аналогією з ceαt для диф. рівнянь 1-го порядку).

Приватні рішення, що відповідають вхідної послідовності x(n)=n+1, шукається у виді y*(n)=An+B

Підставляючи обидва рішення по черзі в однорідне і неоднорідне рівняння і дорівнюючи коефіцієнти при рівних ступенях n, знаходять загальне рішення виду y(n)=n/a+b+A(-B)n, де a, b, A, B- числа.

Перевірка вираження для n=1, 2, 3,... дозволяє переконатися в повному збігу аналітичного рішення з безпосередньою прямою підстановкою.

Імпульсною характеристикою ЛЦФ g(n) називають відгук на δ- вхідну послідовність (за аналогією з аналоговими колами й аналоговими сигналами) при нульових умовах.

     
 


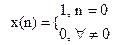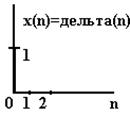Знайдемо ІX ЛЦФ 1-го порядку. Нехай

 


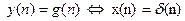Тоді

 


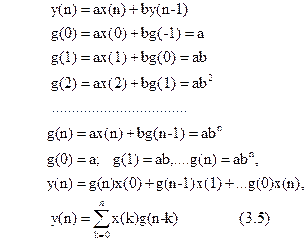Це дискретна згортка вхідної послідовності з імпульсною характеристикою.

 

АНАЛІЗ ЛЦФ МЕТОДОМ Z- ПЕРЕТВОРЕННЯ

При великих порядках фільтрів аналітичний розрахунок ЛЦФ у часовій області скрутний, як і у випадку аналогових ланцюгів.

У цьому випадку звертаються до дискретного аналізу перетворення Лапласа, а саме до Z- перетворення, що переводить аналіз в область комплексної дискретної частоти Z.

Будь-яку послідовність x(nΔt) можна представити у виді:

 


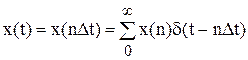
Застосуємо перетворення Лапласа до останнього рівняння:


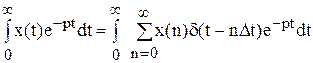
Перетворимо праву частину, виносячи за знак інтегралу незалежні від t величини:


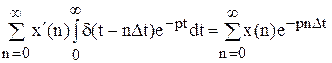
т.к. не власний інтеграл у теорії безупинних функцій дорівнює:


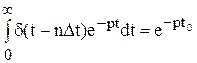
Уведемо позначення:


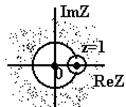
Розглянемо геометричну интерпретацию подібної заміни p→z

 


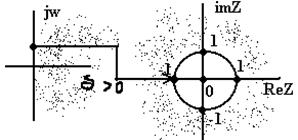Права напівплощина трансформується в зовнішню область окружності, ліва – у внутрішню, а ймовiрна вісь j – у саму окружність одиничного радіуса з центром у т. (0;0).

Т.о., будь-якiй дискретнiй послідовності x(n) можна поставити її пряме Z- перетворення:


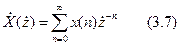
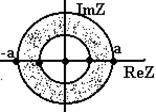
Приклад: Розглянемо дискретний сигнал x(n), знайдемо Z- перетворення

заданої послідовності по формулі (10.7);


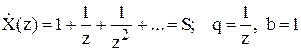
Воно є сумою геометричної прогресії зі знаменником <1 і сходиться при будь-яких z у кільці |z|>1. Підсумовуючи прогресію одержуємо:

 


 

 


 

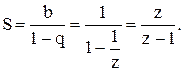На границі області аналiтичности ця функція має один простий полюс у т. z=1.

 


Аналогічно виходить Z- перетворення нескінченного дискретного сигналу x(n)=(1, a, a2,…),де a – деяке дійсне число.

 


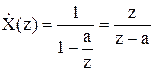По формулі (3.7) одержуємо область збіжності ряду – кільце |z|>a.

Представимо Z- перетворення довільної послідовності x(n) як розкладання в ряд Лорана функції X(z):


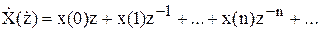
Чудова властивість Z- перетворення полягає в тім, що вихідна послідовність x(n) є відліковими коефіцієнтами цього ряду Лорана. Ми знаємо формулу визначення коефіцієнтів ряду Лорана як інтеграла по замкнутому контурі, рівного сумі відрахувань підінтегральної функції. Т.е. згадана властивість Z- перетворення дозволяє нам вирішити зворотню задачу: по Z- перетворенню відшукати саму вихідну послідовність x(n):


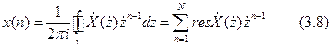
де γ – контур, що охоплює всі полюсы функції X(z). Співвідношення(3.8) зворотне Z- перетворення.

 

Приклад: Нехай задане Z- перетворення вхідного сигналу.

Потрібно знайти вихідний сигнал.

Функція x(z) (x(z)=(z+1)/z) аналитична на всій площині, за винятком т. z=0. Звертаючи до формули (3.8), знайдемо:


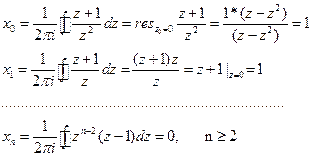
Вихідний сигнал має вид x(n)=(1,1,0,0,0,…)...

Розглянемо найважливіші властивості Z-перетворення: вони аналогічні властивостям Лапласа:

1) Лінійність.

Якщо X1(n) і X2(n) – числові послідовності, що відображають дискретні сигнали Z-перетворення, що мають, X1(z) і X2(z), то лінійна комбінація сигналів

 


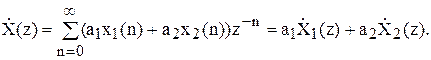X3(n)=a1x1(n)+a2x2(n) має Z-перетворення у виді лінійної комбінації їхніх Z-перетворень.

2) Теорема зсуву. (Z-перетворення зміщеного сигналу)

Нехай x2(n) отриманий з x1(n) зсувом останнього убік запізнювання на одну позицію: x2(n)=x1(n-1).

Безпосереднє обчислення Z-перетворення приводить до результату:

X2(z)=x1(z)z-1, при запізнюванні на m позицій:

X2(z)=x1(z)z-m, еквівалентно множенню перетворення на z-m.

3) Теорема про згорток.

Z-перетворення дискретної згортки 2-х послідовностей дорівнює добутку Z-перетворень цих послідовностей:


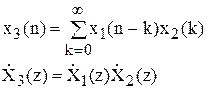
На підставі викладених властивостей сформулюємо алгоритм аналізу ЛЦФ методом Z -перетворення.

Користаючись теоремою про згорток, можна записати Z-перетворення вихідного сигналу через добуток Z-перетворень вхідного сигналу й імпульсної характеристики ЛЦФ.

Визначення. Z-перетворення імпульсної характеристики називають передатною функцією ЛЦФ чи його системною функцією.

За аналогією з рівнянням згортки сигналів у часовій області

для перебування вихідної послідовності Y(z)=G(z)X(z) необхідно визначити:

1) Z-перетворення вхідної послідовності x(n)

2)
Передатну функцію G(z) по відомій імпульсній характеристиці g(n)

3)
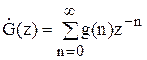
Z-перетворення вихідної послідовності

4)
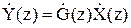
Саму вихідну послідовність


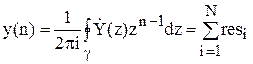
за допомогою теореми про лишки.

Способи визначення передатної функції ЛЦФ.

1) Прямим Z-перетворенням імпульсної характеристики ЛЦФ:

2)
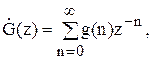
По різницевому рівнянню.

Нехай рекурсивний ЛЦФ описується різницевим рівнянням виду:


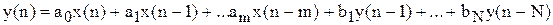
Застосувавши до рівняння Z-перетворення, одержимо.


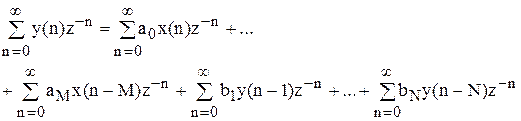
кожна з напівнескінченних сум дорівнює: (користаючись властивістю лінійності і теоремою зсуву)


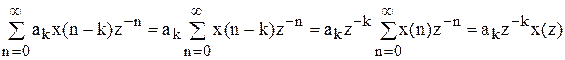
для трансверсальної частини суми.


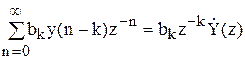
для рекурсивної частини суми.

Таким чином, Z-перетворення різницевого рівняння:


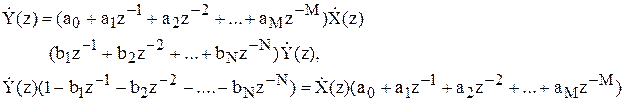
Маємо передатну функцію ЛЦФ:


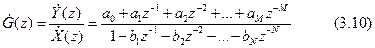
Вираження (3.10) має велике значення, тому що зв'язуючи передатну функцію і різницеве рівняння ЛЦФ, дозволяє вирішити також і зворотню задачу – по передатній функції ЛЦФ G(z) знайти його різницеве рівняння і по ньому побудувати структурну схему фільтра. Задачі подібного типу (установлення структури по характеристиках) звуться задач синтезу, чи в даному випадку задач реал i зац ii ЛЦФ.

По вираженню типу (3.10) будується різницеве рівняння виду


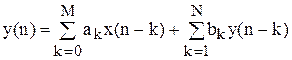
Приклад: Реалізуємо фільтр із передатною функцією

G(z)=(2z-1+1)/(4z-2+4z-1+2).

Розділивши вираження на коефіцієнт при z-1 у чисельнику, маємо


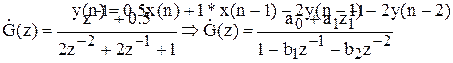
Тобто M=1; a0=0.5; a1=1; N=2; b1=-2; b2=-2, і

 


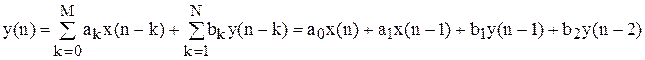Побудуємо по різницевому рівнянню структурну схему ЛЦФ.

 

 


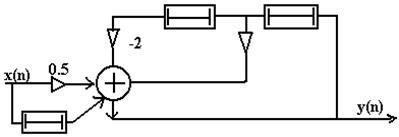Рис.3.1

Приклад. Знайдемо вихідний сигнал методом Z-перетворення побудованого ЛЦФ. Подамо на його вхід послідовність x(n)=(1/2)n і визначимо y(n).

1) Z-перетворення вхідної послідовності

2)
Як пам'ятаємо, передатна функція

3)
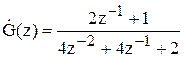
Z-перетворення вхідного сигналу:

 


 

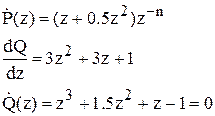4) Вихідна послідовність сигналу:

 

 


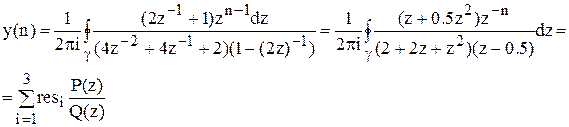
Знайдемо полюси підінтегральної функції – корені знаменника: 2+2z+z2=0,

 


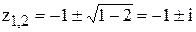z-0.5=0, тоді z3=0.5

 

Знайдемо лишки:


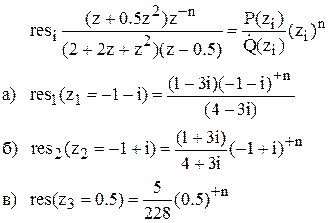
Представляючи комплексні числа в показовій формі *ρeiφ знайдемо

 

 


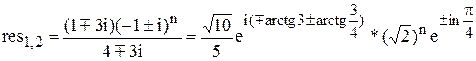
Вихідна послідовність як сума лишкiв res1, res2, res3 дорівнює:


 


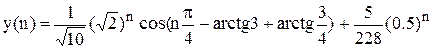
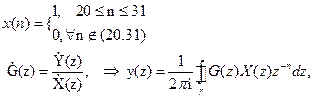Знайти y(n), якщо

Приклад Нехай дана передатна функція ЛЦФ у виді

 

 


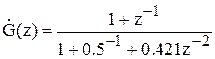
хоча легше в даному випадку побудувати y(n) по різницевому рівнянню, користаючись передатною функцією:


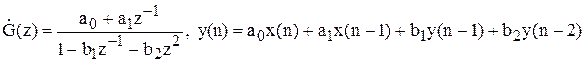
y(n)=x(n)+1*x(n-1)-0.5y(n-1)-0.421y(n-2)

Побудуємо структурну схему ЛЦФ по різницевому рівнянню.

 


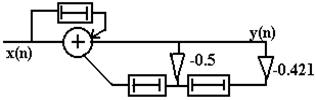Рис.3.2

 

Розрахунок ЛЦФ (перетворення y(n) по x(n)) можна реалізувати у виді програми розрахунку y(n) по різницевому рівнянню, задаючи у виді масиву x(n) – вхідну послідовність і знаходячи масив y(n) – вихідну послідовність.

 

Опис лабораторної установки

Лабораторна установка складається з комп’ютера і програмного забезпечення у вигляді двох середовищ аналізу і проектування –математичного процесора MathCad і програми моделювання електронних схем Electronis Work Bench.

 

Розрахункове завдання

 

1. Методом різницевих рівнянь, користуючись математичним процесором MathCad, розрахувати для схеми, що наведено на рис.3.1, сигнал з виходу ЛЦФ, якщо на вхід подається сигнал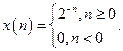

2. ЛЦФ завданий своєю передавальною (системною) функцією G(z)= 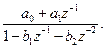. Синтезувати електричну схему фільтра. Визначити його імпульсну характеристику g(n). 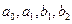визначаються номером залікової книжки: 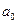-останній,. 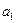-передостанній і т.д.

3. По схемі на рис.3.2 знайти імпульсну характеристику ЛЦФ і для вхідної дії у вигляді 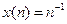методом дискретної згортки знайти відгук y(n).

4. Методом z-перетворень знайти відгук ЛЦФ, що завданий своєю імпульсною характеристикою 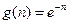. Синтезувати схему фільтра. Визначити передавальну функцію G(z).

5. Змоделювати ЛЦФ у програмному середовищі Electronics Work Bench.

 

 

Лабораторне завдання

 

Наступні завдання виконуються за допомогою математичного процесора MathCad. Всі графіки побудувати для перших тридцяти дискретних відліків часу n.

 

1. ЛЦФ задається своєю передавальною функцією 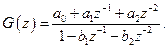Знайти різницеве рівняння y(n), імпульсну характеристику g(n), синтезувати електричну схему. Побудувати графіки.

2. Імпульсна характеристика ЛЦФ має вигляд: 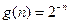. Побудувати електричну схему. Для зовнішньої дії типу 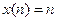знайти відгук фільтра y(n). Побудувати графіки.

3. Побудувати схеми рекурсивного та нерекурсивного ЛЦФ другого порядку. Знайти по них імпульсну та перехідну характеристики цих фільтрів.

4. Для схеми ЛЦФ, зображеної на рис.3.1, знайти амплітудно – частотну та фазо – частотну характеристики і побудувати їх.

5. Знайти умови, при виконанні яких ЛЦФ, що зображений на рис.3.2, стає цифровим резонатором.

6. Методом z – перетворень проаналізувати ЛЦФ, схема якого зображена на рис.3.2. На вході діє сигнал 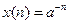. Знайти імпульсну, перехідну характеристики та передавальну функцію цього фільтра.

Вимоги до звіту

Звіт повинен вміщувати в собі:

1. Результати розрахунків та виконання лабораторного завдання.

2. Всі вхідні і вихідні послідовності повинні бути відображені графічно як дискретні функції часу.

 

3. Для кожного ЛЦФ потрібно навести електричну схему

 

Контрольні запитання

1. Що таке лінійний цифровий фільтр? Різновиди ЛЦФ.

2. Запишіть різницеве рівняння рекурсивного та нерекурсивного ЛЦФ.

3. Побудуйте канонічну схему ЛЦФ другого порядку. Поясніть принцип її формування , записавши різницеві рівняння та їх z- перетворення.

4. Запишіть системну функцію ЛЦФ. Як вона пов’язана із імпульсною характеристикою?

5. Зв’язок між комплексним коефіцієнтом передачі і системною функцією.

6. Запишіть зв’язок між імпульсною та перехідною характеристиками ЛЦФ.

7. Поясніть, чому амплітудно- та фазо-частотні характеристики ЛЦФ є періодичними функціями частоти.

8. Як отримати вихідний сигнал, маючи імпульсну характеристику і знаючи вхідну дію?

9. Умови фізичної реалізованості ЛЦФ.

10. Аналіз ЛЦФ методом z- перетворень.

11. Аналіз ЛЦФ методом аналітичного розв’язку різницевих рівнянь.

4 ЛАБОРАТОРНА РОБОТА №4. НЕЛІНІЙНЕ РЕЗОНАНСНЕ ПІДСИЛЕННЯ ТА МНОЖЕННЯ ЧАСТОТИ

 

Ціль роботи – дослідження нелінійного резонансного підсилювача та множника частоти, отримання коливальних характеристик нелінійного підсилювача та коефіцієнта підсилення в режимі подвоєння і потроєння частоти.

 

Короткі теоретичні відомості

Принципова схема нелінійного резонансного підсилювача наведена на рис.4.1. Режим роботи нелінійного резонансного підсилювача ілюструє рис.4.2.

 


 

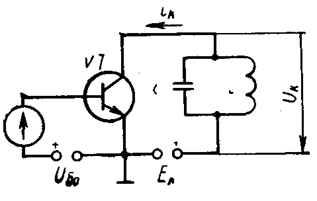Рис.4.1

Нехай на вході підсилювача діє напруга

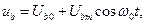(4.1)

де 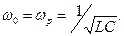При цьому струм, що протікає у вихідному колі підсилювача

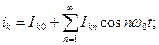(4.2)

напруга на виході підсилювача, якщо вихідний контур настроєний у резонанс на одну із гармонік,

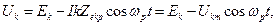(4.3)

де 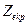- еквівалентний опір паралельного контура при резонансі; 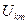- амплітуда напруги на виході підсилювача при резонансі.

Кусочно-лінійна апроксимація вольт-амперної характеристики прямої передачі підсилювача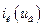

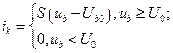(4.4)

 

дозволяє знайти амплітуди гармонійних складових струму як функції гута відсічки :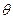

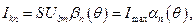(4.5)

 

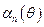де і 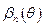- коефіцієнти розвинення косинусоїдального імпульса в ряд Фур’є. Кут відсічки знаходять із співвідношення:

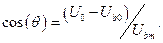(4.6)

Коефіцієнти розвинення в ряд Фур’є 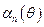досягають максимальних значень при кутах відсічки

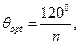(4.7)

 

а коефіцієнти 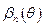- при

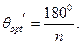(4.8)

При аналізі нелінійних кіл з резонансним навантаженням квазілінійним методом вводяться характеристики і параметри нелінійного елемента для гармоніки, що нас цікавить. Так, параметром транзистора по першій гармоніці в схемі рис.4.1 є середня крутизна

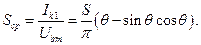(4.9)

Коефіцієнт підсилення нелінійного резонансного підсилювача по першій гармоніці

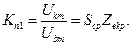(4.10)