Рис.2 Пример зеркальной симметрии
Осевая симметрия:
Фигура называется симметричной относительно прямой А, если для каждой точки фигуры симметричная ей точка относительно прямой А также принадлежит этой фигуре.
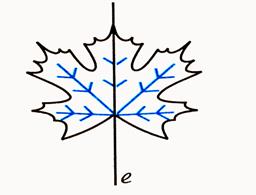
Рис. 3 Пример осевой симметрии
Центральная симметрия:
Центральной симметрией относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что A — середина отрезка XX′. Центральная симметрия с центром в точке A обычно обозначается черезZA {\displaystyle Z_{A}}ZZ, в то время как обозначениеSA {\displaystyle S_{A}} можно перепутать с осевой симметрией. Фигура называется симметричной относительно точки A, если для каждой точки фигуры симметричная ей точка относительно точки A также принадлежит этой фигуре. Точка A называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией. Другие названия этого преобразования - симметрия с центром A. Центральная симметрия в планиметрии является частным случаем поворота, точнее, является поворотом на 180 градусов.
ТЕОРЕМА 1:Центральная симметрия — перемещение.
ТЕОРЕМА 2:Перемещение пространства является центральной симметрией тогда и только тогда, когда оно изменяет направления на противоположные.
ТЕОРЕМА 3:Центральная симметрия переводит прямую в себя или в параллельную ей прямую, плоскость — в себя или в параллельную ей плоскость.
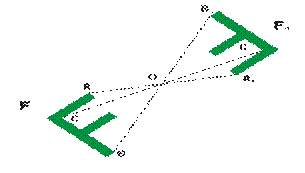
Рис. 4 Пример центральной симметрии
Скользящая симметрия:
Скользящая симметрия - изометрия евклидовой плоскости. Скользящей симметрией называют композицию симметрии относительно некоторой прямой L {\displaystyle l}и переноса на вектор, параллельный {\displaystyle l}LLLl L (этот вектор может быть и нулевым). Скользящую симметрию можно представить в виде композиции 3 осевых симметрий (теорема Шаля)
ТЕОРЕМА: Скользящую симметрию можно представить в виде композиции трех осевых симметрий.
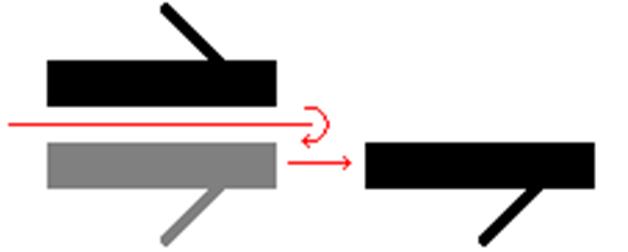
Рис. 5 Пример скользящей симметрии
Вращательная симметрия:
Вращательная симметрия - симметрия объекта относительно всех или нескольких собственных вращений. Преобразование, при котором каждая точка А фигуры проворачивается на один и тот же угол α вокруг заданного центра О, называется вращением или поворотом плоскости. Точка О называется центром вращения, а угол α - угол вращения.
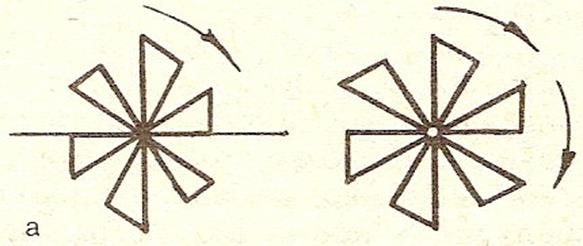
Рис. 6 Пример вращательной симметрии
Переносная симметрия:
Этот вид симметрии состоит в том, что части целой формы организованы таким образом, что каждая следующая повторяет предыдущую и отстоит от нее на определенный интервал в определенном направлении. Этот интервал называют шагом симметрии. Прямая АВ называется осью переноса, а расстояние а –элементарным переносом или периодом.
Переносная симметрия обычно используется при построении бордюров. В произведениях архитектурного искусства ее можно увидеть в орнаментах или решетках, которые используются для их украшения. Переносная симметрия используются и в интерьерах зданий.
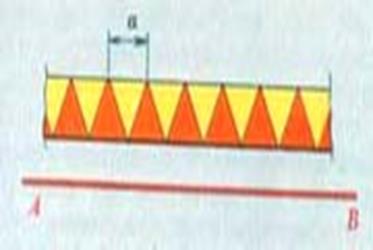
Рис. 7 Пример переносной симметрии
2. СИММЕТРИЯ В АРХИТЕКТУРЕ
Архитектура - это строительное искусство, умение проектировать и создавать города, жилые дома, общественные и производственные здания, площади, улицы и парки. Во многих городах мира можно встретить церкви, дворцы и особняки, современные здания театров, библиотек перед которыми захочется остановиться и повнимательнее их рассмотреть. Это потому что здания и улицы своей красотой могут волновать воображение и чувства человека, как и другие произведения искусства. Шедевры архитектуры запоминаются как символы народов и стран. Всему миру известны Кремль и Красная площадь в Москве, Эйфелева башня в Париже, древний Акрополь в Афинах. Однако в отличие от других искусств, произведения архитектуры люди не только созерцают, но и постоянно используют. Архитектура окружает нас и образует пространственную среду для жизни и деятельности людей.
Симметрия в архитектуре является мощным инструментом эмоционального восприятия города на местности. Данное понятие проходит сквозь многовековой период человеческого творчества, противостоит хаосу, разрухе. Она – гарант уравновешенности, упорядоченности. Симметричность вездесуща, разнообразна. Для создания определенной атмосферы, зодчие используют множество приемов: криволинейность, чередование пространств, сочетание различных объемов. Самым сильным является использование одинаковых фрагментов, плоскостей. Здания получаются уравновешенными, понятными, простыми для интуитивного восприятия.








