Производные и дифференциалы высших порядков.
Пусть функция f(x)- дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную
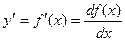
Если найти производную функции f¢(x), получим вторую производную функции f(x).
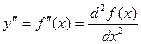
т.е. y¢¢ = (y¢)¢ или 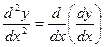 .
.
Этот процесс можно продолжить и далее, находя производные степени n.
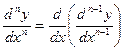 .
.
Производная функции, заданной параметрически.
Пусть 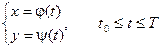
Предположим, что эти функции имеют производные и функция x = j(t) имеет обратную функцию t = Ф(х).
Тогда функция у = y(t) может быть рассмотрена как сложная функция y = y[Ф(х)].
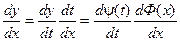
т.к. Ф(х) – обратная функция, то 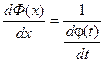
Окончательно получаем: 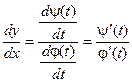
Таким образом, можно находить производную функции, не находя непосредственной зависимости у от х.
50. Теоремы о среднем. Правило Лопиталя-Бернулли. Формулы Тейлора и МакЛорена.
Теорема Роля: Если функция f(x) непрерывна на отрезке [a,b], дифференцируема на интервале (a,b) и на концах отрезка принимает одинаковые значения f(a)=f(b), то найдется хотя бы одна точка 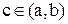 , в которой производная
, в которой производная 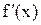 обращается в ноль, т.е.
обращается в ноль, т.е. 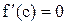 .
.
Теорема Коши: Если функции f(x) и 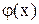 непрерывны на отрезке [a,b], дифференцируемы на интервале (a,b), причем
непрерывны на отрезке [a,b], дифференцируемы на интервале (a,b), причем 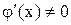 для
для 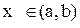 , то найдется хотя бы одна точка
, то найдется хотя бы одна точка 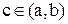 , такая, что выполняется равенство
, такая, что выполняется равенство 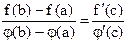 .
.
Теорема Лагранжа:Если функция f(x) непрерывна на отрезке [a,b], дифференцируема на интервале (a,b), то найдется хотя бы одна точка 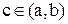 такая, что выполняется равенство
такая, что выполняется равенство 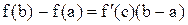 . Это так же является формулой о конечном приращении: приращение дифференцируемой функции на отрезке [a,b] равно приращению аргумента, умноженному на значение производной функции в некоторой точке этого отрезка. Если производная функции равна нулю на некотором промежутке, то функция постоянна на этом промежутке. Если две функции имеют равные производные на некотором промежутке, то они отличаются друг от друга на постоянное слагаемое. Правило Лопиталя (по раскрытию неопределенностей вида 0/0) : Пусть функции f(x) и
. Это так же является формулой о конечном приращении: приращение дифференцируемой функции на отрезке [a,b] равно приращению аргумента, умноженному на значение производной функции в некоторой точке этого отрезка. Если производная функции равна нулю на некотором промежутке, то функция постоянна на этом промежутке. Если две функции имеют равные производные на некотором промежутке, то они отличаются друг от друга на постоянное слагаемое. Правило Лопиталя (по раскрытию неопределенностей вида 0/0) : Пусть функции f(x) и  непрерывны и дифференцируемы в окрестности точки
непрерывны и дифференцируемы в окрестности точки  и обращаются в ноль в этой точке: f(
и обращаются в ноль в этой точке: f(  )=
)=  . Пусть
. Пусть 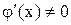 в окрестности точки
в окрестности точки  . Если существует предел
. Если существует предел 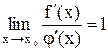 , то
, то 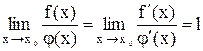 .
.
Правило Лопиталя (по раскрытию неопределенностей вида 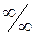 ) : Пусть функции f(x) и
) : Пусть функции f(x) и 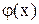 непрерывны и дифференцируемы в окрестности точки
непрерывны и дифференцируемы в окрестности точки  (кроме, может быть, точки
(кроме, может быть, точки  ), в этой окрестности
), в этой окрестности 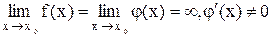 . Если существует предел
. Если существует предел 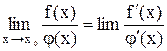 .
.
51.Монотонность функции. Экстремум. Необходимые и достаточные условия.
Теорема(необходимые условия). Если дифференцируемая на интервале (a,b) функция f(x) возрастает (убывает), то 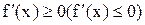 для любых
для любых 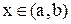 . Док-во. Пусть функция f(x) возрастает на интервале (a,b). Возьмем произвольные точки х и х +
. Док-во. Пусть функция f(x) возрастает на интервале (a,b). Возьмем произвольные точки х и х + 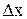 на интервале (a,b) и рассмотрим отношение
на интервале (a,b) и рассмотрим отношение 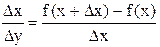 . Функция f(x) возрастает, поэтому если
. Функция f(x) возрастает, поэтому если 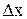 >0, то x+
>0, то x+ 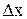 >x и f(x+
>x и f(x+ 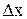 )>f(x); если
)>f(x); если 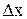 <0, то x+
<0, то x+ 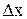 >x и f(x+
>x и f(x+ 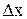 )<f(x). В обоих случаях
)<f(x). В обоих случаях 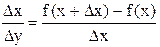 >0, так как числитель и знаменатель дроби имеют одинаковые знаки. По условию теоремы функция f(x) имеет производную в точке x и является пределом рассматриваемого отношения. Следовательно,
>0, так как числитель и знаменатель дроби имеют одинаковые знаки. По условию теоремы функция f(x) имеет производную в точке x и является пределом рассматриваемого отношения. Следовательно, 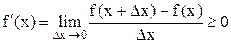 . Аналогично рассматриваем тот случай, когда функция f(x) убывает на интервале (a,b). Данная теорема означает, что касательные к графику возрастающей дифференцируемой функции образуют острые углы с положительным направлением оси Ox или в некоторых точках параллельны оси Ox.
. Аналогично рассматриваем тот случай, когда функция f(x) убывает на интервале (a,b). Данная теорема означает, что касательные к графику возрастающей дифференцируемой функции образуют острые углы с положительным направлением оси Ox или в некоторых точках параллельны оси Ox.
Теорема(достаточные условия). Если функция f(x) дифференцируема на интервале (a,b) и 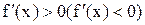 для
для 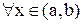 , то эта функция возрастает (убывает) на интервале (a,b). Док-во. Пусть
, то эта функция возрастает (убывает) на интервале (a,b). Док-во. Пусть 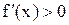 . Возьмем точки
. Возьмем точки 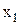 и
и 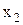 из интервала (a,b), причем
из интервала (a,b), причем 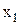 >
> 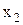 . Применим к отрезку [
. Применим к отрезку [ 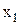 ,
, 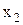 ] теорему Лагранжа: f(
] теорему Лагранжа: f( 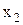 ) - f(
) - f( 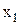 )=
)= 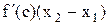 , где
, где 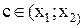 . По условию
. По условию 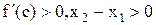 . Следовательно, f(
. Следовательно, f( 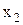 ) - f(
) - f( 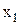 )>0 или f(
)>0 или f( 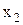 )>f(
)>f( 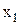 ), т.е. функция f(x) на интервале (a,b) возрастает. Возрастающая или убывающая функция называется монотонной. Теорема (необходимое условие экстремума). Если дифференцируемая функция y=f(x) имеет экстремум в точке
), т.е. функция f(x) на интервале (a,b) возрастает. Возрастающая или убывающая функция называется монотонной. Теорема (необходимое условие экстремума). Если дифференцируемая функция y=f(x) имеет экстремум в точке  , то ее производная в этой точке равна нулю:
, то ее производная в этой точке равна нулю: 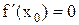 . Док-во: Пусть, для определенности,
. Док-во: Пусть, для определенности,  -точка максимума. Значит, в окрестности точки
-точка максимума. Значит, в окрестности точки  выполняется неравенство
выполняется неравенство 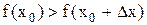 . Но тогда
. Но тогда 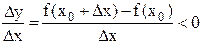 , если
, если 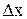 >0, и
>0, и 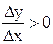 , если
, если 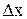 <0. По условию теоремы производная
<0. По условию теоремы производная 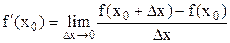 существует. Переходя к пределу, при
существует. Переходя к пределу, при 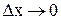 , получим
, получим 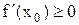 , если
, если 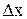 <0 и
<0 и 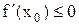 , если
, если 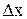 >0. Поэтому :
>0. Поэтому : 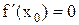 . Теорема (достаточное условие экстремума): Если непрерывная функция f(x) дифференцируема в некоторой
. Теорема (достаточное условие экстремума): Если непрерывная функция f(x) дифференцируема в некоторой 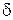 -окрестности и критической точки
-окрестности и критической точки  и при переходе через нее 9слева направо) производная
и при переходе через нее 9слева направо) производная 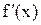 меняет знак с плюса на минус, то
меняет знак с плюса на минус, то  есть точка максимума; с минуса на плюс, то
есть точка максимума; с минуса на плюс, то  -точка минимума. Док-во: рассмотрим
-точка минимума. Док-во: рассмотрим 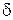 -окрестность точки
-окрестность точки  . Пусть выполняются условия:
. Пусть выполняются условия: 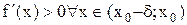 и
и 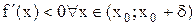 . Тогда функция f(x) возрастает на интервале
. Тогда функция f(x) возрастает на интервале 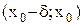 , а на интервале
, а на интервале 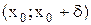 она убывает. Отсюда следует, что значение f(x) в точке
она убывает. Отсюда следует, что значение f(x) в точке  является наибольшим на интервале
является наибольшим на интервале 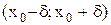 , т.е. f(x)<f(
, т.е. f(x)<f(  ) для всех
) для всех 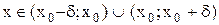 . Это и означает, что
. Это и означает, что  - точка максимума функции.
- точка максимума функции.
52. Выпуклость, вогнутость, точки перегиба. Необходимые и достаточные условия. Асимптоты. Общая схема исследования функции.
- График функции y=f(x) назыв. выпуклым (вверх) на отрезке [a,b], если он расположен ниже касательной. Для дифференцируемой на [a,b] функции график расположен ниже любой касательной; для недифференцируемой функции график расположен выше хорды((a, f(a) и (b, f(b))).
- График функции назыв. вогнутым (выпуклым вниз) на [a,b], если он расположен выше касательной (ниже хорды). Если в левой U(  ) график функции выпуклый в одну сторону, а в правой окрестности в другую сторону, то
) график функции выпуклый в одну сторону, а в правой окрестности в другую сторону, то  -точка перегиба.
-точка перегиба.
- Если функция y=f(x) дважды дифференцируема на [a,b] и для любых 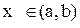
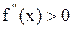 , то график является выпуклым вниз(вогнутым). Если
, то график является выпуклым вниз(вогнутым). Если 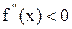 , то график является выпуклым. Достаточное условие точки перегиба: Пусть f - дважды дифференцируемая функция в окрестности
, то график является выпуклым. Достаточное условие точки перегиба: Пусть f - дважды дифференцируемая функция в окрестности  и
и 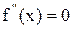 или
или 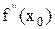 не существует. Если при этом для любых
не существует. Если при этом для любых 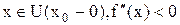 , а для любых
, а для любых 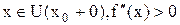 , то
, то  - точка перегиба.
- точка перегиба.
Асимптоты. При исследовании поведения графика функции либо в бесконечности, либо вблизи точек разрыва второго рода часто оказывается, что график приближается к некоторой прямой линии. Другими словами, расстояние между точками графика функции и точками прямой линии, измеренные по вертикали и горизонтали, стремится к нулю. Такие прямые линии – асимптоты графика функции. Бывают вертикальные (точки разрыва 2ого рода), либо наклонные (поведение функции в бесконечности). Горизонтальная асимптота – частный случай наклонной. Непрерывные функции не имеют вертикальных асимптот. Для того, чтобы график функции y=f(x) имел наклонную асимптоту y=kx+b, необходимо и достаточно, чтобы существовали конечные пределы 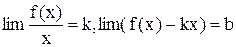 .
.
Общая схема исследования функции. 1. Находим область определения D(x). 2. Находим точки разрыва второго род, обозначаем вертикальные асимптоты. 3. Исследуем функцию на четность/нечетность, периодичность. 4. Находим точки пересечения с Ox и Oy. С Ox: x=o, y-?. C Oy: y=0, x-? 5. Находим наклонные асимптоты, если они есть. 6. Исследуем функцию на наличие критических точек. Решаем уравнение 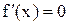 . 7. Определяем промежутки монотонности. 8. Находим вторую производную и точки, для которых она равна 0 или не существует. 9. Находим промежутки знакопостоянства второй производной. 10. Составляем таблицу. 11. на основе таблицы определяем точки локального экстремума и точки перегиба.
. 7. Определяем промежутки монотонности. 8. Находим вторую производную и точки, для которых она равна 0 или не существует. 9. Находим промежутки знакопостоянства второй производной. 10. Составляем таблицу. 11. на основе таблицы определяем точки локального экстремума и точки перегиба.
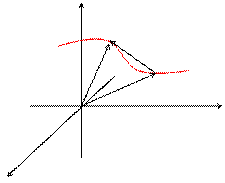
53. Вектор-функция скалярного аргумента. Годограф. Производная. Касательная прямая и нормальная плоскость.
Векторная функция скалярного аргумента.
 |
A(x, y, z)
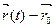
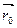
Пусть некоторая кривая в пространстве задана параметрически: x = j(t); y = y(t); z = f(t); Радиус- вектор произвольной точки кривой: 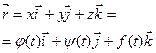 .
.
Таким образом, радиус- вектор точки кривой может рассматриваться как некоторая векторная функция скалярного аргумента t. При изменении параметра t изменяется величина и направление вектора 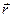 . Запишем соотношения для некоторой точкиt0:
. Запишем соотношения для некоторой точкиt0: 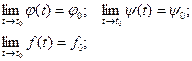 Тогда вектор
Тогда вектор 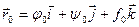 - предел функции
- предел функции 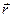 (t).
(t). 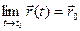 . Очевидно, что
. Очевидно, что 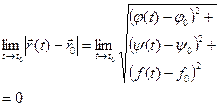 , тогда
, тогда 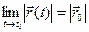 . Чтобы найти производную векторной функции скалярного аргумента, рассмотрим приращение радиус- вектора при некотором приращении параметра t.
. Чтобы найти производную векторной функции скалярного аргумента, рассмотрим приращение радиус- вектора при некотором приращении параметра t.
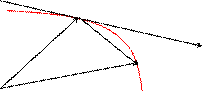
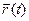
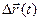
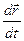
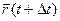
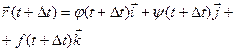 ;
; 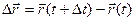 ;
;
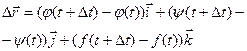
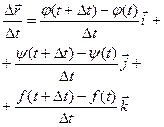
или, если существуют производные j¢(t), y¢(t), f¢(t), то 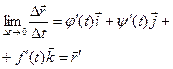 .
.
Это выражение – вектор производная вектора 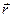 .
. 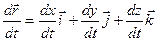 ;
; 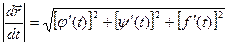 . Если имеется уравнение кривой: x = j(t); y = y(t); z = f(t); то в произвольной точке кривой А(xА, yА, zА) с радиус- вектором
. Если имеется уравнение кривой: x = j(t); y = y(t); z = f(t); то в произвольной точке кривой А(xА, yА, zА) с радиус- вектором 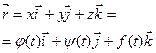
можно провести прямую с уравнением 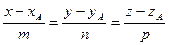 . Т.к. производная
. Т.к. производная 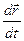 - вектор, направленный по касательной к кривой, то
- вектор, направленный по касательной к кривой, то 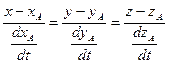 . Уравнение нормальной плоскости к кривой будет иметь вид:
. Уравнение нормальной плоскости к кривой будет иметь вид: 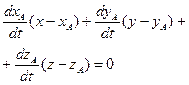 .
.
Определение: Линия, которую опишет в пространстве переменный радиус – вектор  при изменении параметра S, называется годографом этого вектора.
при изменении параметра S, называется годографом этого вектора.  , тогда
, тогда 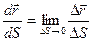 - вектор, направленный по касательной к кривой в точке А(x, y, z). Но т.к.
- вектор, направленный по касательной к кривой в точке А(x, y, z). Но т.к. 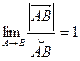 , то
, то 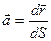 - единичный вектор, направленный по касательной. Если принять
- единичный вектор, направленный по касательной. Если принять 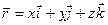 , то
, то 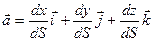 .
.
Причем 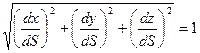 . Рассмотрим вторую производную
. Рассмотрим вторую производную 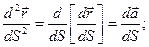
Определение: Прямая, имеющая направление вектора 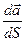 называется главной нормалью к кривой. Ее единичный вектор обозначается
называется главной нормалью к кривой. Ее единичный вектор обозначается 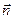 .
. 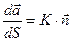 , где К – кривизна кривой.
, где К – кривизна кривой. 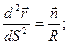
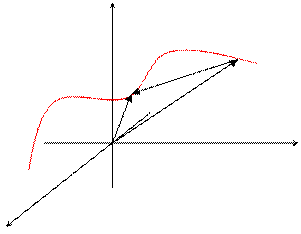
54. Кривизна и кручение. Кривизна пространственной кривой.
 z
z
B
A(x, y, z) 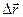
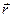
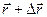
0 y
x
Для произвольной точки А, находящейся на пространственной кривой, координаты могут быть определены как функции некоторой длины дуги S.
x = j(S); y = y(S); z = f(S); 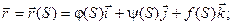 Приведенное выше уравнение называют векторным уравнением линии в пространстве.
Приведенное выше уравнение называют векторным уравнением линии в пространстве.
Определение: Линия, которую опишет в пространстве переменный радиус – вектор 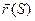 при изменении параметра S, называется годографом этого вектора.
при изменении параметра S, называется годографом этого вектора. 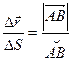 , тогда
, тогда 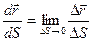 - вектор, направленный по касательной к кривой в точке А(x, y, z). Но т.к.
- вектор, направленный по касательной к кривой в точке А(x, y, z). Но т.к. 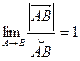 , то
, то 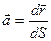 - единичный вектор, направленный по касательной. Если принять
- единичный вектор, направленный по касательной. Если принять 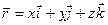 , то
, то 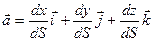 . Причем
. Причем 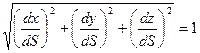 . Рассмотрим вторую производную
. Рассмотрим вторую производную 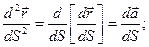 Определение: Прямая, имеющая направление вектора
Определение: Прямая, имеющая направление вектора 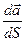 называется главной нормалью к кривой. Ее единичный вектор обозначается
называется главной нормалью к кривой. Ее единичный вектор обозначается 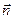 .
.
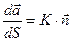 , где К – кривизна кривой.
, где К – кривизна кривой. 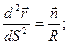 Кривизна пространственной кривой может быть найдена по формуле:
Кривизна пространственной кривой может быть найдена по формуле: 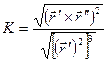 Возможна и другая запись формулы для кривизны пространственной кривой (она получается из приведенной выше формулы):
Возможна и другая запись формулы для кривизны пространственной кривой (она получается из приведенной выше формулы):
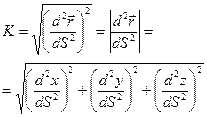 Определение: Вектор
Определение: Вектор 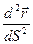 называется вектором кривизны. Величина
называется вектором кривизны. Величина 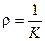 называется радиусом кривизны.
называется радиусом кривизны.
Величина 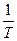 называется кручением кривой.
называется кручением кривой.
55. Сопровождающий трёхгранник Френе. Формулы Френе.
Под трёхгранником Френе, иначе называемым естественным, сопровождающим или сопутствующим трёхгранником или репером, понимают тройку векторов 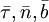 сопоставленную каждой точке гладкой кривой, где
сопоставленную каждой точке гладкой кривой, где  — единичный касательный вектор,
— единичный касательный вектор, 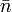 — единичный вектор главной нормали,
— единичный вектор главной нормали, 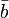 — единичный вектор бинормали к кривой в данной точке. Если s — натуральный параметр вдоль кривой, то векторы
— единичный вектор бинормали к кривой в данной точке. Если s — натуральный параметр вдоль кривой, то векторы 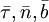 вязаны соотношениями:
вязаны соотношениями:
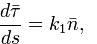
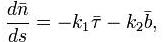
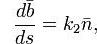
называемыми формулами Френе и задающими натуральное уравнение кривой.
56. Предел, непрерывность и частные производные функции нескольких переменных.
Для функции двух переменных вводится понятие предела функции непрерывности, аналогично случаю функции одной переменной. Введем понятие окрестности точки. Множество всех точек М(x,y) плоскости, координаты которых удовлетворяют неравенству 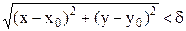 , называется
, называется 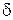 -окрестностью точки
-окрестностью точки 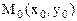 . Другими словами,
. Другими словами, 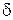 -окрестность точки
-окрестность точки 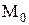 - это все внутренние точки круга с центром
- это все внутренние точки круга с центром 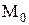 и радиусом
и радиусом 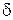 . Пусть функция z=f(x,y) определена в некоторой окрестности точки
. Пусть функция z=f(x,y) определена в некоторой окрестности точки 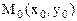 , кроме, быть может, самой это точки. Число А называется пределом функции z=f(x,y) при
, кроме, быть может, самой это точки. Число А называется пределом функции z=f(x,y) при 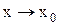 и
и 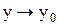 , если для любого
, если для любого 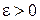 существует
существует 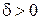 такое, что для всех
такое, что для всех 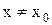 и
и 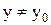 и удовлетворяющих неравенству
и удовлетворяющих неравенству 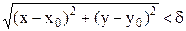 выполняется неравенство
выполняется неравенство 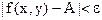 . Записывают:
. Записывают: 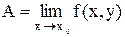 или
или 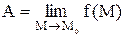 .Из определения следует, что если предел существует, то он не зависит от пути, по которому М стремится к
.Из определения следует, что если предел существует, то он не зависит от пути, по которому М стремится к  (число таких направлений бесконечно). Геометрический смысл предела функции: каково бы ни было число
(число таких направлений бесконечно). Геометрический смысл предела функции: каково бы ни было число 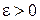 , найдется
, найдется 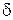 -окрестность точки
-окрестность точки 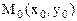 , что во всех ее точках
, что во всех ее точках 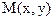 , отличных от
, отличных от 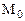 , аппликаты соответствующих точек поверхности z=f(x,y) отличаются от числа А по модулю меньше, чем на
, аппликаты соответствующих точек поверхности z=f(x,y) отличаются от числа А по модулю меньше, чем на 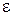 . Непрерывность функции двух переменных. Функция z=f(x,y)(или f(M)) называется непрерывной в точке
. Непрерывность функции двух переменных. Функция z=f(x,y)(или f(M)) называется непрерывной в точке 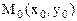 , если она: а)определена в этой точке и некоторой ее окрестности; б)имеет предел
, если она: а)определена в этой точке и некоторой ее окрестности; б)имеет предел 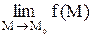 ; в)этот предел равен значению функции z в точке
; в)этот предел равен значению функции z в точке 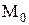 , т.е.
, т.е. 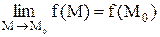 или
или 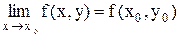 . Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается, называются точками разрыва этой функции. Точки разрыва z=f(x,y) могут образовывать целые линии разрыва. Так, функция
. Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается, называются точками разрыва этой функции. Точки разрыва z=f(x,y) могут образовывать целые линии разрыва. Так, функция 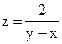 имеет линию разрыва y=x. Функция z=f(x,y) называется непрерывной в точке
имеет линию разрыва y=x. Функция z=f(x,y) называется непрерывной в точке 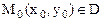 , если выполняется равенство
, если выполняется равенство 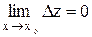 , т.е. полное приращение функции в этой точке стремится к нулю, когда приращения ее аргументов x и y стремятся к нулю.
, т.е. полное приращение функции в этой точке стремится к нулю, когда приращения ее аргументов x и y стремятся к нулю.
Частные производные нескольких переменных. Пусть задана функция z=f(x,y). Т.к. x и y – независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной x приращение 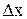 , сохраняя значение y неизменным. Тогда z получит приращение, которое называется частным приращением z по x и обозначается
, сохраняя значение y неизменным. Тогда z получит приращение, которое называется частным приращением z по x и обозначается 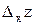 . Итак,
. Итак, 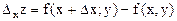 . Аналогично получаем частное приращение z по y:
. Аналогично получаем частное приращение z по y: 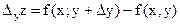 . Полное приращение
. Полное приращение 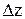 функции z определяется равенством
функции z определяется равенством 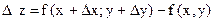 . Если существует предел
. Если существует предел 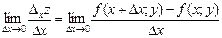 , то он называется частной производной функции z=f(x,y) в точке M(x,y) по переменной x и обозначается
, то он называется частной производной функции z=f(x,y) в точке M(x,y) по переменной x и обозначается 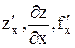 . Частные производные по x в точке
. Частные производные по x в точке 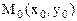 обычно обозначают символами
обычно обозначают символами 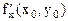 .
.
57. Полный дифференциал. Производные высших порядков.
Пусть функция z=f(x;y) определена в некоторой окрестности точки M(x,y). Составим полное приращение функции в точке М: 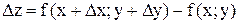 . Функция x=f(x,y) называется дифференцируемой в точке M(x,y), если ее полное приращение в этой точке можно представить в виде:
. Функция x=f(x,y) называется дифференцируемой в точке M(x,y), если ее полное приращение в этой точке можно представить в виде: 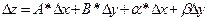 , где
, где 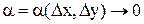 и
и 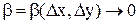 при
при 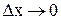 ,
, 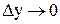 . Сумма первых двух слагаемых в равенстве представляет собой главную часть приращения функции. Главная часть приращение функции z=f(x;y), линейная относительно
. Сумма первых двух слагаемых в равенстве представляет собой главную часть приращения функции. Главная часть приращение функции z=f(x;y), линейная относительно 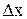 и
и 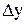 , называется полным дифференциалом этой функции и обозначается символом dz: dz= A*
, называется полным дифференциалом этой функции и обозначается символом dz: dz= A* 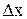 +B*
+B* 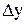 . Выражения A*
. Выражения A* 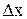 и B*
и B* 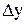 называют частными дифференциалами. Для независимых переменных x и y полагают
называют частными дифференциалами. Для независимых переменных x и y полагают 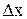 =dx и
=dx и 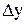 =dy. Поэтому равенство можно переписать в виде: dz=A*dx+B*dy.
=dy. Поэтому равенство можно переписать в виде: dz=A*dx+B*dy.
Полный дифференциал функции называют также дифференциалом первого порядка. Пусть функция z=f(x,y) имеет непрерывные частные производные второго порядка. Дифференциал второго порядка определяется по формуле 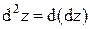 .Найдем его:
.Найдем его: 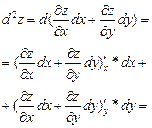
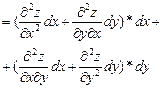 .
.
Отсюда:
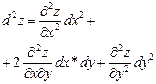 . Символически это записывается так:
. Символически это записывается так: 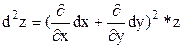 . Аналогично можно получить формулу для дифференциала третьего порядка:
. Аналогично можно получить формулу для дифференциала третьего порядка: 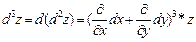 . Получается, что:
. Получается, что: 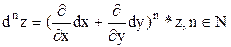
58. Касательная плоскость и нормаль к поверхности. Экстремум функции нескольких переменных.
Пусть функция z=f(x,y) дифференцируема в точке 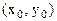 некоторой области
некоторой области 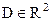 . Рассечем поверхность S, изображающую функцию z, плоскостями x=
. Рассечем поверхность S, изображающую функцию z, плоскостями x=  и y=
и y= 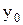 . Плоскость x=
. Плоскость x=  пересекает поверхность S по некоторой линии
пересекает поверхность S по некоторой линии 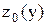 , уравнение которой получается подстановкой в выражение исходной функции z=f(x,y) вместо х числа
, уравнение которой получается подстановкой в выражение исходной функции z=f(x,y) вместо х числа  . Точка
. Точка 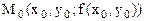 принадлежит кривой
принадлежит кривой 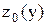 . В силу дифференцируемости функции z в точке
. В силу дифференцируемости функции z в точке 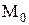 функция
функция 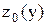 также является дифференцируемой в точке y=
также является дифференцируемой в точке y= 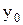 . Следовательно, в этой точке в плоскости x=
. Следовательно, в этой точке в плоскости x=  к кривой
к кривой 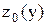 может быть проведена касательная
может быть проведена касательная 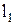 . Построим касательную
. Построим касательную 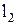 к кривой
к кривой 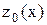 в точке x=
в точке x=  . Прямые
. Прямые 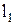 и
и 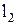 определяют плоскость
определяют плоскость 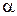 , которая называется касательной плоскостью к поверхности S в точке
, которая называется касательной плоскостью к поверхности S в точке 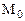 . Составим ее уравнение. Так как плоскость
. Составим ее уравнение. Так как плоскость 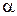 проходит через точку
проходит через точку 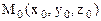 , то ее уравнение может быть записано в виде А(
, то ее уравнение может быть записано в виде А( 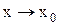 ) + В(
) + В( 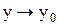 ) + С(
) + С( 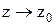 )=0, которое можно переписать так:
)=0, которое можно переписать так: 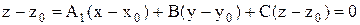 (разделив уравнение на –С и обозначив А/-С=
(разделив уравнение на –С и обозначив А/-С= 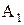 , В/-С=
, В/-С= 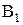 ). Найдем
). Найдем 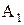 и
и 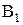 . Уравнения касательных имеют вид:
. Уравнения касательных имеют вид: 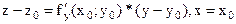 ;
; 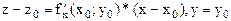 соответственно. Касательная
соответственно. Касательная 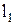 лежит в плоскости
лежит в плоскости 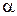 .
. 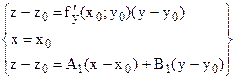 . В итоге
. В итоге 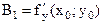 . Следовательно,
. Следовательно, 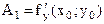 . Искомое уравнение касательной плоскости:
. Искомое уравнение касательной плоскости: 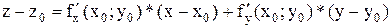 . Прямая, проходящая через точку
. Прямая, проходящая через точку 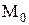 и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется ее нормалью. Каноническое уравнение нормали:
и перпендикулярная касательной плоскости, построенной в этой точке поверхности, называется ее нормалью. Каноническое уравнение нормали: 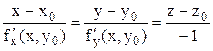 .
.
Экстремум ф-ции нескольких переменных. Теорема(необходимые условия экстремума): Если в точке N(  ,
, 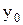 ) дифференцируемая функция z=f(x,y) имеет экстремум, то ее частные производные в этой точке равны нулю:
) дифференцируемая функция z=f(x,y) имеет экстремум, то ее частные производные в этой точке равны нулю: 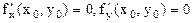 . Док-во: Зафиксируем одну из переменных. Положим, y=
. Док-во: Зафиксируем одну из переменных. Положим, y= 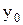 . Тогда получим ф-цию
. Тогда получим ф-цию 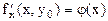 одной переменной, которая имеет экстремум при x-
одной переменной, которая имеет экстремум при x-  . Следовательно, согласно необходимому условию экстремума функции одной переменной,
. Следовательно, согласно необходимому условию экстремума функции одной переменной, 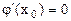 , т.е.
, т.е. 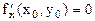 . Замеч.: ф-ция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. Точка, в которой частные производные первого порядка функции z=f(x,y) равны нулю, т.е.
. Замеч.: ф-ция может иметь экстремум в точках, где хотя бы одна из частных производных не существует. Точка, в которой частные производные первого порядка функции z=f(x,y) равны нулю, т.е. 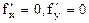 , называется стационарной точкой функции z. Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками. В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума. Теорема(достаточное условие экстремума): Пусть в стационарной точке
, называется стационарной точкой функции z. Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками. В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума. Теорема(достаточное условие экстремума): Пусть в стационарной точке 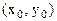 и некоторой ее окрестности функция F(x,y) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке
и некоторой ее окрестности функция F(x,y) имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке 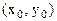 значения
значения 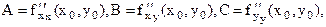 обозначим
обозначим 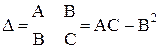 . Тогда: 1.Если
. Тогда: 1.Если 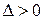 , то функция f(x,y) в точке
, то функция f(x,y) в точке 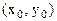 имеет экстремум: максимум, если A<0, минимум, если A>0; 2.Если
имеет экстремум: максимум, если A<0, минимум, если A>0; 2.Если 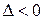 , то функция f(x,y) в точке
, то функция f(x,y) в точке 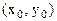 экстремума не имеет. В случае
экстремума не имеет. В случае 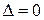 экстремум в точке
экстремум в точке 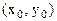 может быть, может не быть. Необходимы дополнительные исследования.
может быть, может не быть. Необходимы дополнительные исследования.
59. Условный экстремум функции нескольких переменных. Наибольшее и наименьшее значение функции нескольких переменных в области.








