Производная сложной функции.
Теорема. Пусть y = f ( x ); u = g ( x ), причем область значений функции u входит в область определения функции f .
Тогда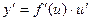 
Доказательство .
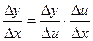
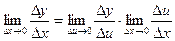
( с учетом того, что если Dx®0, то Du®0, т.к. u = g(x) – непрерывная функция)
Тогда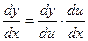 
. Теорема доказана.
Дифференциал сложной функции.
Инвариантная форма записи дифференциала.
Пусть y = f ( x ), x = g ( t ), т.е у- сложная функция.
Тогда dy = f ¢ ( x ) g ¢ ( t ) dt = f ¢ ( x ) dx.
Видно, что форма записи дифференциала dy не зависит от того, будет ли х независимой переменной или функцией какой- то другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала.
Однако, если х- независимая переменная, то
dx = Dx, но
если х зависит от t, то Dх ¹ dx.
Таким образом форма записи dy = f¢(x)Dx не является инвариантной.
48.правила дифференцирования. Производные основных элементарных функций. Логарифмическое дифференцирование.
Основные правила дифференцирования.
Обозначим f ( x ) = u , g ( x ) = v- функции, дифференцируемые в точке х.
1) (u ± v) ¢ = u ¢ ± v ¢
2) (u × v) ¢ = u × v ¢ + u ¢ × v
3) 
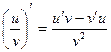, если v ¹ 0
Эти правила могут быть легко доказаны на основе теорем о пределах.
Производные основных элементарных функций.
1)С¢ = 0; 9)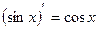 
2)(xm)¢ = mxm-1;
10) 
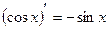
3) 
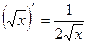
11) 
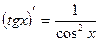
4) 
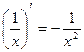
12) 
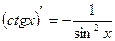
5) 
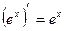
13) 
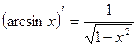
6) 
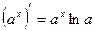
14) 
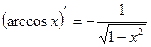
7) 
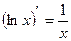
15) 
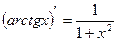
8) 
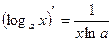
16) 
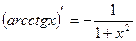
Логарифмическое дифференцирование.
Рассмотрим функцию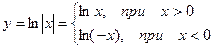 
.
Тогда (lnïxï)¢=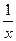 
, т.к. 
.
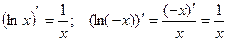Учитывая полученный результат, можно записать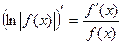 
.
Отношение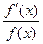 
называется логарифмической производной функции f(x).
Способ логарифмического дифференцирования состоит в том, что сначала находят логарифмическую производную функции, а затем производную самой функции по формуле
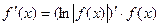
Способ логарифмического дифференцирования удобно применять для нахождения производных сложных, особенно показательных функций, для которых непосредственное вычисление производной с использованием правил дифференцирования представляется трудоемким.
49. производные и дифференциалы высших порядков. Производная параметрически заданных функций.