Эллиптический цилиндр
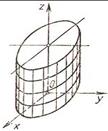 Эллиптическое уравнение:
Эллиптическое уравнение:
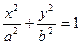
Частным случаем эллиптического цилиндра является круговой цилиндр, его уравнение x2 + y2 = R2. Уравнение x2=2pz определяет в пространстве параболический цилиндр.
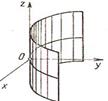
Уравнение: 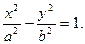 определяет в пространстве гиперболический цилиндр.
определяет в пространстве гиперболический цилиндр.
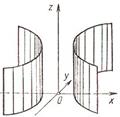
Все эти поверхности называются цилиндрами второго порядка, так как их уравнения есть уравнения второй степени относительно текущих координат x, y, z.
30. графики в полярной системе координат и параметрически заданных функций.
Любая точка на плоскости может быть однозначно определена при помощи различных координатных систем, выбор которых определяется различными факторами. Способ задания начальных условий для решения какой – либо конкретной технической задачи может определить выбор той или иной системы координат. Для удобства проведения вычислений часто предпочтительнее использовать системы координат, отличные от декартовой прямоугольной системы. Кроме того, наглядность представления окончательного ответа зачастую тоже сильно зависит от выбора системы координат.
Полярная система координат.
Точка О называется полюсом, а луч l – полярной осью.
Суть задания какой- либо системы координат на плоскости состоит в том, чтобы каждой точке плоскости поставить в соответствие пару действительных чисел, определяющих положение этой точки на плоскости. В случае полярной системы координат роль этих чисел играют расстояние точки от полюса и угол между полярной осью и радиус– вектором этой точки. Этот угол j называется полярным углом.
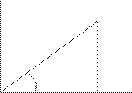
Можно установить связь между полярной системой координат и декартовой прямоугольной системой, если поместить начало декартовой прямоугольной системы в полюс, а полярную ось направить вдоль положительного направления оси Ох.
31. Действительные числа.
Действительные числа образуют совокупность элементов, обладающую следующими свойствами.
Если a и b - действительные числа (алгебраические, рациональные, целые, положительные целые), то таковыми же являются и
1. a + b и ab (замкнутость),
2. a + b = b + a, ab = ba (коммутативность),
3. a + (b + c) = (a + b) + c = a + b + c, a(bc) = (ab)c = abc (ассоциативность
4. a * 1 = a (единица),
5. a(b + c) = ab + ac (дистрибутивность),
6. из a + c = b + c следует a = b, из ca = cb, , следует a = b (сокращение).
Действительное число 0 (нуль) обладает свойствами a + 0 = a, a * 0 = 0 для каждого действительного числа a.
Действительные числа, не являющиеся рациональными, называются иррациональными.
Действительными алгебраическими числами называются действительные корни алгебраических уравнений с целочисленными коэффициентами, а действительными трансцендентными числами - остальные действительные числа.
32. Множества и операции над ними.
Множества – совокупность некоторых объектов, объединенных по какому-то признаку.
Объекты из которых состоит множество, называются элементами. Множества принято обозначать заглавными латинскими буквами А,B,C…,а их элементы - малыми буквами .
Множество, не содержащее ни одного элемента, называется пустым множеством.
Элементы множества записывают в фигурных скобках, внутри которых они перечислены.
Множество А называется подмножеством В, если каждый элемент множества А является элементом множества В.
Множества А и В равны или совпадают, если они состоят из одних и тех же элемнтов.
Объединение – множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств.
Пересечение – множество, состоящее из элементов, каждый из которых принадлежит множеству А и множеству В.
Множества, элементами которых являются числа, называются числовыми.
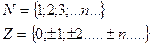
Множество К содержит рациональные и иррациональные числа. Всякое рациональное число выражается или конечной десятичной дробью или бесконечной периодической дробью.
33. Предел последовательности.
Число а называется пределом последовательности, если для любого положительного числа Е найдется такое натуральное число N, что при всех n>N выполняется равенство:
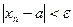 . В этом случае пишут
. В этом случае пишут 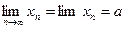 и говорят, что последовательность {xn}имеет предел, равный числу а. говорят,что последовательность сходится к а.
и говорят, что последовательность {xn}имеет предел, равный числу а. говорят,что последовательность сходится к а.
Коротко определение предела: 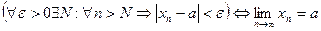 .
.
Сходящаяся последовательность имеет только один предел. Последовательность, неимеющая предела, называется расходящейся.
Если 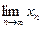 =0 => последовательность бесконечно малая.
=0 => последовательность бесконечно малая.
Если 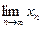 =
= 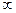 => бесконечно большая.
=> бесконечно большая.
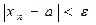 =>
=> 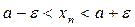 .
.
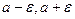 - окрестности точки а.
- окрестности точки а.
34. Теоремы о пределах последовательности.
Теорема 1: (необходимый признак числовой последовательности):
если последовательность сходится, то она ограничена. , если последовательность неограниченна, то она расходится.
Теорема Вейерштрасса: сформируем достаточный признак числовой последовательности: всякая ограниченная монотонная последовательность имеет предел.
Теорема : если две последовательности {xn}и {yn} сходятся, т.е. имеют конечные пределы, то сходятся также сумма, разность, произведение, частное этих последовательностей, т.е.:
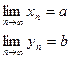 =>
=> 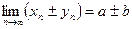 и тд.
и тд.
Теорема: если 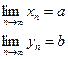 и начиная с некоторого номера выполняется неравенство xn
и начиная с некоторого номера выполняется неравенство xn 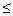 yn, то а
yn, то а 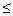 b.
b.
Доказательство:
допустим, что а>b. Из равенств 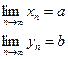 следует, что для любого
следует, что для любого 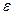 >0 найдется такое натуральное число N(
>0 найдется такое натуральное число N( 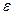 ), что при всех n>N(
), что при всех n>N( 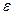 ) будут выполняться неравенства
) будут выполняться неравенства 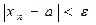 и
и 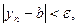 т.е.
т.е.
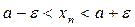 и
и 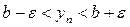 . Возьмем
. Возьмем 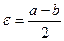 . Тогда:
. Тогда: 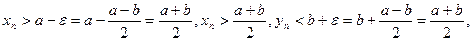 отсюда следует, что xn>yn, это противоречит условию xn
отсюда следует, что xn>yn, это противоречит условию xn 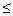 yn следовательно, а
yn следовательно, а 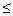 b.
b.
35. Предел функции.
Сформулируем два, эквивалентных между собой, определения предела функции в точке:
Определение ( по Коши): число А называется пределом функции в точке х0 , если для любого положительного 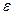 найдется такое положительное число
найдется такое положительное число 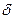 , что для всех х
, что для всех х 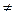 х0 , удовлетворяющих неравенству
х0 , удовлетворяющих неравенству 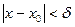 , выполняется неравенство
, выполняется неравенство 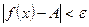 .
.
Коротко это определение:
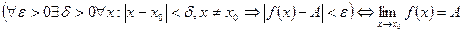 .
.
Определение (по Гейне):
Число А называется пределом функции 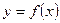 в точке х0, если для любой последовательности допустимых значений аргумента хn, сходящейся к х0, последовательность соответствующих значений функции
в точке х0, если для любой последовательности допустимых значений аргумента хn, сходящейся к х0, последовательность соответствующих значений функции 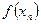 ,
, 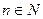 , сходится к числу А.
, сходится к числу А.
Односторонние пределы:
число А называется пределом функции 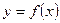 слева в точке x0, если для любого число
слева в точке x0, если для любого число 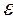 >0 существует число
>0 существует число 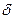 =
= 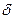 (
( 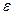 )>0 такое, что при
)>0 такое, что при 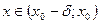 выполняется неравенство
выполняется неравенство 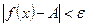 .
.
Предел слева записывают так: 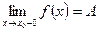
Аналогично определяется предел функции справа:
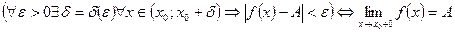 .
.
Пределы функции слева и справа называются односторонними пределами.
Предел функции при 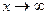 :
:
Число А называется пределом функции при 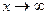 , если для любого положительного числа
, если для любого положительного числа 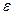 существует такое число М=М(
существует такое число М=М( 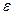 ) >0, что при всех х, удовлетворяющих неравенству
) >0, что при всех х, удовлетворяющих неравенству 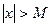 выполняется неравенство
выполняется неравенство 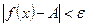 . Коротко:
. Коротко:
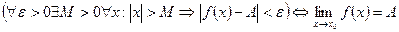
36. Бесконечно малые и бесконечно большие функции.
Функция 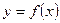 называется бесконечно большой при
называется бесконечно большой при 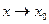 , если для любого числа M>0 существует число
, если для любого числа M>0 существует число 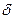 =
= 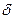 (М)>0, что для всех х, удовлетворяющих неравенству 0<
(М)>0, что для всех х, удовлетворяющих неравенству 0< 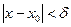 , выполняется неравенство
, выполняется неравенство 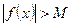 . Записывают
. Записывают 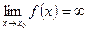 . Коротко:
. Коротко:
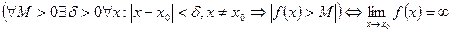
Функция 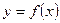 называется бесконечно большой при
называется бесконечно большой при 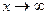 , если для любого числа M>0 найдется такое число N=N (М)>0, что для всех х, удовлетворяющих неравенству
, если для любого числа M>0 найдется такое число N=N (М)>0, что для всех х, удовлетворяющих неравенству 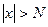 , выполняется неравенство
, выполняется неравенство 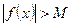 . Коротко:
. Коротко:
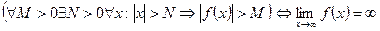
Всякая бесконечно большая функция в окрестности точки х0 является неограниченной в этой окрестности.
Бесконечно малая функция:
Функция 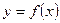 называется бесконечно малой при
называется бесконечно малой при 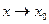 , если
, если 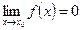 : для любого числа
: для любого числа 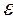 >0 найдется число
>0 найдется число 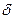 >0 такое, что для всех х, удовлетворяющих неравенству 0<
>0 такое, что для всех х, удовлетворяющих неравенству 0< 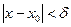 , выполняется неравенство
, выполняется неравенство 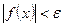 .
.
Теорема: алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
Док-во:
Теорема: произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.
Док-во:
Следствие: так как всякая б.м.ф. ограничена, то из теоремы вытекает произведение двух б.м.ф. есть функция бесконечно малая.
Следствие: произведение б.м.ф. на число есть функция бесконечно малая.
Теорема: частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая.
Док-во:
Теорема: если функция - бесконечно малая, то обратная ей функция – бесконечно большая и наоборот.
Док-во:
37. односторонние пределы.
число А называется пределом функции 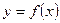 слева в точке x0, если для любого число
слева в точке x0, если для любого число 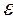 >0 существует число
>0 существует число 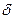 =
= 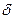 (
( 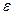 )>0 такое, что при
)>0 такое, что при 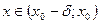 выполняется неравенство
выполняется неравенство 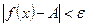 .
.
Предел слева записывают так: 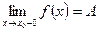
Аналогично определяется предел функции справа:
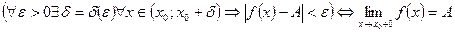 .
.
Пределы функции слева и справа называются односторонними пределами.
38. Сравнение бесконечно малых.
Две б.м.ф. сравниваются между собой с помощью их отношения:
1. если 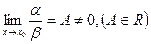 , то
, то 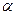 и
и 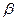 называются бесконечно малыми одного порядка.
называются бесконечно малыми одного порядка.
2. если 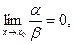 то
то 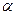 называется бесконечно малой более высокого порядка, чем
называется бесконечно малой более высокого порядка, чем 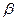 .
.
3. если 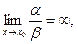 то
то 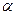 называется бесконечно малой более низкого порядка, чем
называется бесконечно малой более низкого порядка, чем 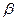 .
.
4. если 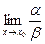 не существует, то
не существует, то 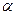 и
и 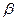 называются несравнимыми бесконечно малыми.
называются несравнимыми бесконечно малыми.
Таковы же правила сравнения б.м.ф. при 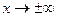 и
и 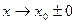 .
.
Эквивалентные бесконечно малые:
| Sinx | x, при 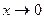
| ex - 1 | x, 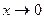
|
| tgx | x, 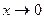
| ax - 1 | x*lna, 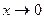
|
| arcsinx | x, 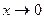
| ln(1+x) | x, 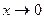
|
| arctgx | x, 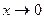
| loga(1+x) | x*logae 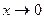
|
| 1-cosx | 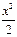 , , 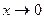
| (1+x)k - 1 | k*x, k>0, 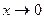
|
39. Теоремы о пределах.
Теорема: если существует 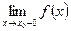 и
и 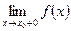 и они равны между собой, то существует
и они равны между собой, то существует 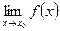 =
= 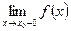
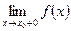 .
.
Теорема: если 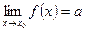 ,
, 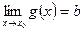 , то =>
, то =>
1) 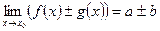
2) 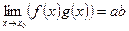
3) 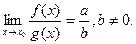
Примечание 1: 1-е и 2-е свойства распространяются на любое конечное число слагаемых или сомножителей, однако число слагаемых и сомножителей не может быть 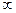 .
.
Примечание 2: 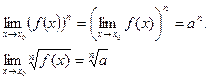
Теорема: если 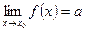 , то функция g(x) = f(x) – a является б.м. при
, то функция g(x) = f(x) – a является б.м. при 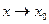 .
.
Следствие: если 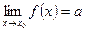 => в окрестности т. х0 g(x) + а = f(x), где g(x)- б.м. при
=> в окрестности т. х0 g(x) + а = f(x), где g(x)- б.м. при 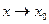 .
.
Теорема: если 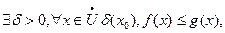 и существуют конечные пределы, когда
и существуют конечные пределы, когда 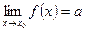 ,
, 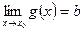 =>
=> 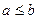 .
.
Теорема (о сжатой переменной): если 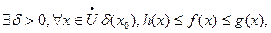 и существуют конечные пределы
и существуют конечные пределы 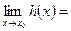
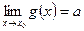 => существует:
=> существует: 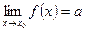 .
.
Теорема (о пределе сложной функции):
Пусть: х0, 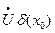 , U=f(x),
, U=f(x), 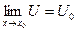 .
.
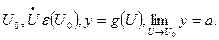
Сама теорема:
Если 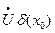 задана сложная функция,
задана сложная функция, 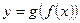 и существуют конечные пределы
и существуют конечные пределы 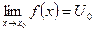 и
и 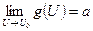 , то
, то 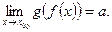
40. первый замечательный предел.
При вычислении пределов выражений, содержащих тригонометрические функции, часто используют предел 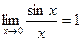 называемый первым замечательным пределом.
называемый первым замечательным пределом.
Читается: предел отноешния синуса к его аргументу равен единице, когда аргумент стремится к нулю.
Доказательство:
Возьмем круг радиуса 1, обозначим радианную меру угла МОВ через х. пусть 0<x< 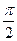 . На рисунке
. На рисунке 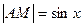 , дуга МВ численно равна центральному углу х,
, дуга МВ численно равна центральному углу х, 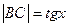 . Очевидно, имеем
. Очевидно, имеем 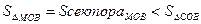 . На основании соответствующих формул геометрии получаем
. На основании соответствующих формул геометрии получаем 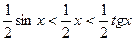 . Разделим неравенство на
. Разделим неравенство на 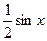 >0, Получим 1<
>0, Получим 1< 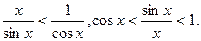
Так как 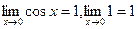 , то по признаку ( о пределе промежуточной функции) существования пределов
, то по признаку ( о пределе промежуточной функции) существования пределов 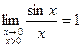 .
.
А если x<0 => 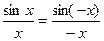 , где –x>0 =>
, где –x>0 => 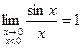
41. Второй замечательный предел.
Как известно, предел числовой последовательности 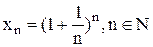 , имеет предел равный e.
, имеет предел равный e. 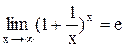 . 1.Пусть
. 1.Пусть 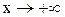 . Каждое значение x заключено между двумя положительными целыми числами:
. Каждое значение x заключено между двумя положительными целыми числами: 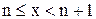 , где n=[x] – это целая часть x. Отсюда следует
, где n=[x] – это целая часть x. Отсюда следует 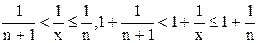 , поэтому
, поэтому 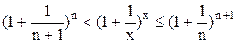 . Если
. Если 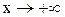 , то
, то 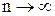 . Поэтому:
. Поэтому: 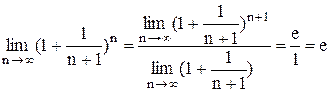 ,
,
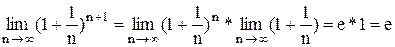 . По признаку существования пределов:
. По признаку существования пределов: 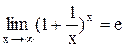 . 2. Пусть
. 2. Пусть 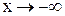 . Сделаем подстановку –x=t, тогда
. Сделаем подстановку –x=t, тогда 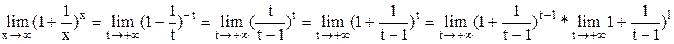 =
= 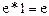 .
. 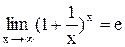 и
и 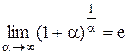 называются вторым замечательным пределом. Они широко используются при вычислении пределов. В приложениях анализа большую роль играет показательная функция с основанием e. Функция
называются вторым замечательным пределом. Они широко используются при вычислении пределов. В приложениях анализа большую роль играет показательная функция с основанием e. Функция 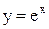 называется экспоненциональной, употребляется также обозначение
называется экспоненциональной, употребляется также обозначение 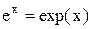 .
.
42. непрерывность функции в точке.
Пусть функция f(x) определена в некоторой окрестности O(x0) точки x0 (включая саму точку x0).
Функция f(x) называется непрерывной в точке x0, если существует 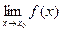 , равный значению функции f(x) в этой точке:
, равный значению функции f(x) в этой точке: 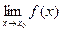 =f(x0).
=f(x0).
Необходимое и достаточное условие непрерывности функции в точке :
Функция y = f(x) непрерывна в точке х0 тогда и только тогда, когда
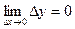
Замечание. Условие можно трактовать как второе определение непрерывности функции в точке. Оба определения эквивалентны.
Пусть функция f(x) определена в полуинтервале [x0, x0 + δ ).
Функция f(x) называется непрерывной справа в точке x0, если существует односторонний предел 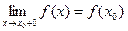
Пусть функция f(x) определена в полуинтервале (x0 − δ, x0].
Функция f(x) называется непрерывной слева в точке x0, если существует односторонний предел
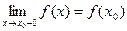
Непрерывность суммы, произведения и частного двух непрерывных функций :
Теорема 1. Если функции f(x) и g(x) непрерывны в точке х0, то в этой точке непрерывны
f(x) ± g(x),
f(x) · g(x),
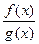 , (g(x0) ≠ 0).
, (g(x0) ≠ 0).
43. классификация точек разрыва.
Рассмотрим некоторую функцию f(x), непрерывную в окрестности точки х0, за исключением может быть самой этой точки. Из определения точки разрыва функции следует, что х = х0 является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной.
Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.
Если односторонний предел 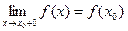 , то функция называется непрерывной справа.
, то функция называется непрерывной справа.

Если односторонний предел 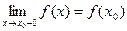 , то функция называется непрерывной слева.
, то функция называется непрерывной слева.
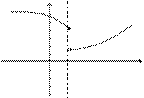
Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.
Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.
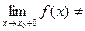
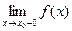
Для выполнения условий этого определения не требуется, чтобы функция была определена в точке х = х0, достаточно того, что она определена слева и справа от нее.
Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
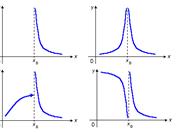
Если значения на концах разрыва совпадают, то для наличия разрыва нужно, чтобы либо эти совпадающие значения были отличны от значения функции в точке , либо функция в этой точке была вовсе не определена. Если в этом случае переопределить (или доопределить) функцию в точке , то полученная изменённая функция будет уже непрерывна в точке и разрыв в точке исчезнет; отсюда и название такого разрыва -- устранимый.
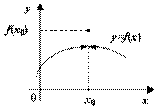 точка устранимого разрыва – когда пределы слева и справа существуют и равны между собой , но не совпадают со значением функции в точке х0 или функция не определена в точке х0.
точка устранимого разрыва – когда пределы слева и справа существуют и равны между собой , но не совпадают со значением функции в точке х0 или функция не определена в точке х0.
44. Теоремы о непрерывных функциях. Непрерывность на отрезке. Равномерная непрерывность.
Теорема: f(x) и g(x) непрерывны в т.х0, то:
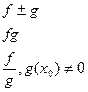 - непрерывны в точке х0.
- непрерывны в точке х0.
Доказательство: : 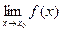 =f(x0).
=f(x0).
: 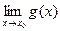 =g(x0).
=g(x0).
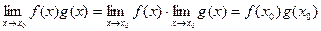 .
.
Следствие 1: любой многочлен является непрерывной функцией любой точки действительной оси.
Следствие 2: любая рациональная функция: 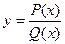 такая, что
такая, что 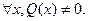 (это значит, что любая рациональная функция может иметь не более чем конечное число т.р.2).
(это значит, что любая рациональная функция может иметь не более чем конечное число т.р.2).
Теорема:( о существовании обратной функции):
если функция y=f(x) непрерывна и строго монотонна на [a,b] оси Ох, то обратная функция 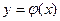 также непрерывна и монотонна на соответствующем отрезке [c,d] оси Оу.
также непрерывна и монотонна на соответствующем отрезке [c,d] оси Оу.
Свойства функций, непрерывных на отрезке:
Теорема (Вейерштрасса): если функция непрерывна на отрезке, то она достигает на этом отрезке своего наибольшего и наименьшего значений.
Следствие: если функция непрерывна на отрезке, то она ограничена на этом отрезке.
Непрерывность функции в интервале и на отрезке:
Функция y=f(x) называется непрерывной в интервале ( a , b ),если она непрерывна в каждой точке этого интервала.
Функция y=f(x) называется непрерывной на отрезке [ a , b ] , если она непрерывна в интервале (a,b) и в точке х=а непрерывна справа (т.е. 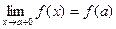 ), а в точке x=b непрерывна слева (
), а в точке x=b непрерывна слева ( 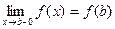 ).
).
Равномерная непрерывность:
Функция f: X → R называется равномерно-непрерывной на множестве X, если
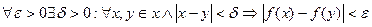 .
.
45. Производная функции, ее геометрический и физический смысл.
Определение. Производной функции f ( x ) в точке х = х0 называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.
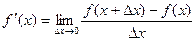
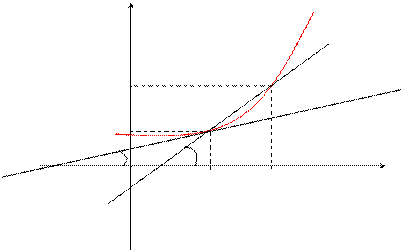
у
f(x)
f(x0 +Dx) P
Df
f(x0) M
a b x 0 x0 Dx x0 + Dx
Пусть f ( x ) определена на некотором промежутке (a, b). Тогда 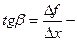 тангенс угла наклона секущей МР к графику функции.
тангенс угла наклона секущей МР к графику функции.

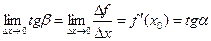 ,
,
где a - угол наклона касательной к графику функции f ( x ) в точке (x0, f(x0)).
Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.
 Уравнение касательной к кривой:
Уравнение касательной к кривой: 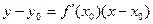
 Уравнение нормали к кривой:
Уравнение нормали к кривой: 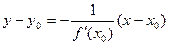 .
.
Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.
Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.
Соответственно, вторая производная функции- скорость изменения скорости, т.е. ускорение.
46. Дифференциал функции.
Пусть функция y = f(x) имеет производную в точке х: 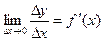
Тогда можно записать: 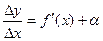 , где a®0, при Dх®0.
, где a®0, при Dх®0.
Следовательно: 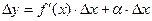 .
.
Величина aDx- бесконечно малая более высокого порядка, чем f¢(x)Dx, т.е. f¢(x)Dx- главная часть приращения Dу.
Определение. Дифференциалом функции f(x) в точке х называется главня линейная часть приращения функции.
Обозначается dy или df(x).
Из определения следует, что dy = f¢(x)Dx или dy = f ¢ ( x ) dx .
 Можно также записать:
Можно также записать: 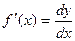
Геометрический смысл дифференциал
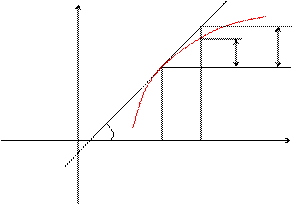 f(x)
f(x)
K dy Dy
M L
a
x x + Dx
Из треугольника DMKL: KL = dy = tg a × D x = y ¢ × D x
Таким образом, дифференциал функции f ( x ) в точке х равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.
Свойства дифференциала.
Если u = f ( x ) и v = g ( x )- функции, дифференцируемые в точке х, то непосредственно из определения дифференциала следуют следующие свойства:
1) d(u ± v) = (u ± v) ¢ dx = u ¢ dx ± v ¢ dx = du ± dv
2) d(uv) = (uv) ¢ dx = (u ¢ v + v ¢ u)dx = vdu + udv
3) d(Cu) = Cdu
Приближенные вычисления с помощью полного дифференциала.
Пусть функция f(x, y) дифференцируема в точке (х, у). Найдем полное приращение этой функции:
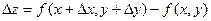
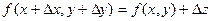
Если подставить в эту формулу выражение
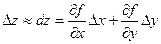
то получим приближенную формулу:
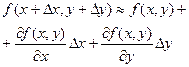
47. производная и дифференциал сложной функции.








