3. Нормальное уравнение плоскости: .

Дата: 2025-05-01; Просмотры: 3

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

4. Угол между двумя плоскостями:

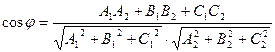
5. расстояние от точки до плоскости:

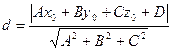
6. Уравнение плоскости в отрезках.

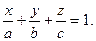
17. Прямая в пространстве.

1. Канонические уравнения прямой линии в пространстве, или уравнения прямой с направляющими коэффициентами, имеют вид:

.

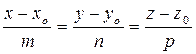где x0, y0, z0 - координаты точки, через которую проходит прямая, а m, n и p - направляющие коэффициенты прямой, которые являются проекциями на координатные оси Ox, Oy, Oz направляющего вектора прямой.

2. В параметрическом виде уравнения прямой линии в пространстве записываются так:

.

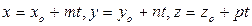3. Общие уравнения прямой:

А₁х +B₁y + C₁z + D₁=0

A₂x + B₂y + C₂z + D₂=0

4. Векторное уравнение прямой:

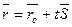
5. уравнение прямой в пространстве, проходящей через две точки:

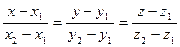
6. угол между прямыми:

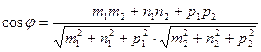
18. взаимное расположение плоскостей.

Угол между двумя плоскостями. Условия параллельности и перпендикулярности двух плоскостей:
пусть заданы две плоскости Q₁ и Q₂:

А₁х +B₁y + C₁z + D₁=0

A₂x + B₂y + C₂z + D₂=0

Под углом между плоскостями понимается один из двугранных углов, образованных этими плоскостями.

.

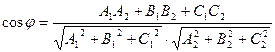Если плоскости перпендикулярны, то таковы же их нормали, т.е. 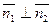. Но тогда 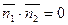,т.е.

A₁A₂ + B₁B₂ + C₁C₂ = 0. Полученное равенство есть условие перпендикулярности двух плоскостей.

Если плоскости параллельны, то будут параллельны и их нормали. Но тогда, как известно, координаты векторов пропорциональны: 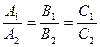. Это и есть условие параллельности двух плоскостей.

19. Взаимное расположение прямых.

Угол между прямыми. Условия параллельности и перпендикулярности прямых.

Пол углом между этими прямыми понимают угол между направляющими векторами S₁ и S₂.

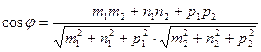
Для нахождения острого угла между прямыми L₁ и L₂ числитель правой части формулы следует взять по модулю.

Если прямые L₁ и L₂ перпендикулярны, то в этом и только в этом случае имеем cos 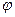=0. следовательно, числитель дроби = 0, т.е. 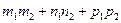=0.

Если прямые L₁ и L₂ параллельны, то параллельны их направляющие векторы S₁ и S₂. следовательно, координаты этих векторов пропорциональны: .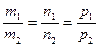

Условие, при котором две прямые лежат в одной плоскости:

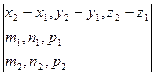=0.

При выполнении этого условия прямые либо лежат в одной плоскости, то есть либо пересекаются.

20. Взаимное расположение прямой и плоскости.