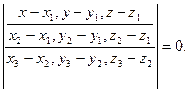Правило решения СУ.
1)найти ранг основной и расширенной матрицы (если rA не =rA с крыш, то система несовместна.
2) если rA=rA с крыш и =r, то система совместна и надо найти базисный минор порядка r.
3)Берём r ур-ий из коэф которых составлен базисн минор. Остальные ур-ия отбрасываем. Неизвестные, коэф которых входят в минор наз главными. Из оставл слева, а остальные (n-r) – справа.
4)Найти выражения главных неизв через свободные. Получено общее решение системы
5)Придавая свободным низвестным произвольное значение, получим соотв значения главн неизв, т.е. найдём частные решения.
9. Однородные СЛАУ. Фундаментальная система решений.
АХ=В – система и параллельно рассмотрим систему АХ=0. (АХ=В – Неоднородн. СЛАУ, АХ=0 – однородн. СДАУ).
Одновременно выполняется:
1. АХ=0 имеет тольок тривиальное решение, АХ=В имеет единственное решение или не имеет решений совсем.
2. АХ=0 имеет нетривиальное решение, АХ=В имеет бесконечное число решений.
Рассмотрим подробнее 2-ой случай: r(A) = r(A с волной сверху)<m..
M – r(A) – дефект, количество свободных неизвестных.
Пример:
,
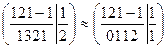б.м: х1, х2
св.м: х3, х4.
х2 + х3 +2х4 = 1., х2 = 1 – а – 2b, х3 = а, х4 = b.
х1 = -2х2 – х3 + х4 + 1 = -2 + 2а +4b – а + b+1 = -1 + а + 5b.
Ответ: (-1 + а + 5b., 1 – а – 2b , а, b)Т.
Хо – общее решение ОСЛАУ
Х (с волной) – общее решение НСЛАУ
10. Векторы на плоскости и в пространстве. Операции над векторами.
Вектор – направленный отрезок, т.е. раз есть слово отрезок, значит есть начало и конец.
1. перенос отрезка при помощи параллельного переноса, не изменяет вектор.
2. вектор задается «длиной вектора» и направления.
3. если у вектора изменить направление на противоположное, то получаем противоположный вектор.
4. нулевой вектор – вектор, длина которого = 0 или начальная конечная точки совпадают. ( у нулевого вектора направление неопределенно).
Коллинеарные векторы – векторы, у которых задающие их отрезки параллельны одной и той же прямой.
Примечание: если из двух коллинеарных векторов направление одинаковое, то вектора сонаправленные, а если противоположные, то называется противоположно-направленные.
Компланарные векторы – векторы, у которых задающие их отрезки параллельны одной и той же плоскости.
Примечание: два вектора в пространстве всегда компланарны.
Примечание: два вектора называются равными, если они сонаправлены и равны по длине.
Линейные операции над векторами:
1. умножение вектора на число:
Результатом будет вектор, коллинеарный исходному (соноправленный в случае положительного множителя и противоположно-направленный – в случае отрицательного множителя), длина которого равна произведению модуля числового множителя на длину исходного модуля.
2. сумма двух векторов:
Есть вектор, получаемый из слагаемых при помощи правила параллелограмма или правила треугольника.
11. Коллинеарность и компланарность. Базис. Координаты.
Коллинеарные векторы – векторы, у которых задающие их отрезки параллельны одной и той же прямой.
Примечание: если из двух коллинеарных векторов направление одинаковое, то вектора сонаправленные, а если противоположные, то называется противоположно-направленные.
Компланарные векторы – векторы, у которых задающие их отрезки параллельны одной и той же плоскости.
Примечание: два вектора в пространстве всегда компланарны.
Примечание: два вектора называются равными, если они сонаправлены и равны по длине.
Базис пространства -совокупность лин независ векторов, по которым можно разложить любой вектор этого пр-ва.
Базис 3 x мерного пр-ва образует любая тройка некомпланарных векторов пр-ва.
Если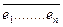 
образуют базис в пространстве, то любой вектор 
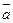из этого пространства может быть представлен: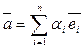 
Примечание: для конкретно-заданного базиса не всегда просто бывает найти коэффициент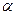 
.
Проще всего это сделать когда базис является ортонормированным.
Понятие ортонормированности распадается на понятия ортогональности и нормированности.
( перпендикулярность и длина=1).
В 3-х мерном пространстве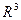 
ортогональный базис состоит из 3 взаимноперпендикулярных векторов.
Ортонормированный базис состоит из 3-х взаимноперпендикулярных векторов, длина каждого из которых = 1.
12. Скалярное произведение векторов. Определение. Вычисление. Свойства.
Скалярное произведение векторов - число = произвед длин на косинус между ними.
Скалярное произ 2х векторов = модулю одного умноженного на проекцию другого на соноправленную с 1-ым вектором ось.
Свойства:
1.a*b=b*a
2. (C*a)*b=C*(a*b)
3. a(b+c)=a*c+b*c;
4. 
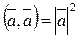
5. (a, b) = 0 =>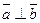 
6. ij = jk = kj = 0.
Теорема 1: в пространстве R3 в ортонормированном базисе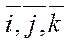 
:
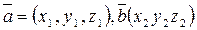
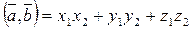
Следствие из Т1: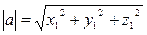 
Для вектора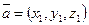 
: 
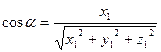
Механический смысл скалярного произведения:
Пусть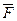 
- сила, которая перемещает тело в направлении вектора S ( на длину 
) =>
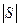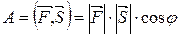
13. векторное произведение векторов. Определение. Вычисление. Свойства.
Три некомпланарных вектора a, b, с взяты в указанном порядке и образуют правую тройку, если с конца 3-его вектора с кратчайший поворот от 1-ого a ко 2-ому b видим совершающийся против часовой стрелки, и левую – если по часовой.
Векторное произведение вектора a на b - это c, который:
1)с перпендикулярно a и b;
2)имеет длину, численно равную площади параллельного, параллелограмма на векторах |c|=|a|*|b|*sinσ; 3) векторы a, b, с образ правую тройку.
Замечание: Из определения вытекает след соотношения между ортами ijk:
1. i*j=k;
2. j*k=i;
3. k*i=j;
Свойства:
1)векторное произ при перестановке множителей меняет знак. (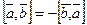 
)
2)два ненулевых вектора коллинеарны, когда их векторное произв =0.
Пункты: 1)условие коллиниарности: a//b => a*b=0;
2)нахождение S параллелограмма и S треуг. Sпар=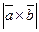 
sin 
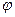. Sтр=0,5*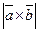 
3)определение момента силы. |M|=|F|*|S|.
Теорема:
, 
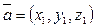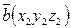
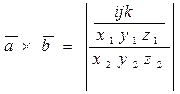
14. Смешанное произведение векторов. Определение. Вычисление. Свойства.
Смешанное произведение 3х векторов равно объёму параллелепипеда, построенного на этих векторах, взятого со знаком + (-), если эти векторы образуют правую (левую) тройку.
Свойства:
1)смешанное произв не меняется при циклической перестановке его множителей.
( 
.
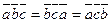2)смешанное произв меняет знак при перемене мест любых букв любых сомножителей
3)смешанное произ ненулевых векторов =0 тога, когда они компланарны.
Смешанное произ векторов = определителю 3-его порядка, составленного из координат перемноженных векторов.
Приложение. 1)определение взаимных ориентаций векторов в пространстве: если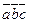 
>0 ( 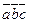<0), то правая (левая) тройка векторов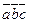
2)комплонарность векторов: 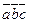компланарны, когда их произв =0.
3)Геометрический смысл: Vпараллелепипеда= 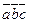. Vтр=1/6( ).
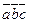Вычисление: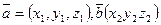 
, 
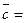
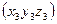
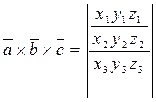
15. Прямая на плоскости.
Простейшей из линий является прямая. Разным способам задания прямой соответствует в прямоугольной система координат разные виды ее уравнений.
1. Уравнение прямой с угловым коэффициентом:
Пусть: tg 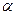=k,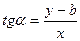 
, тогда: y = kx + b.
Число tg 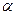=k называется угловым коэффициентом прямой, а уравнение – уравнением прямой с угловым коэффициентом.
2. Уравнение прямой, проходящей через данную точку в данном направлении
Пусть прямая проходит через точку М(Хо,Уо) и ее направление характеризуется угловым коэффициентом к.
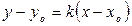
Уравнение с различными значениями к называют также уравнениеми пучка прямых с центром в точке М(Хо,Уо).
3. Уравнение прямой, проходящей через две точки.
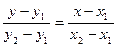, уравнение прямой, проходящей через две точки М1(х1, у1) и М2(х2,у2)
4. Уравнение прямой в отрезках.
Пусть прямая пересекает ось Ох в точке М1(а,0), а ось Оу – в точке М2(0, b)
В этом случае уравнение примет вид: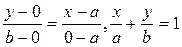 
4. уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
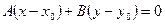- уравнение прямой, проходящей через заданную точку перпендикулярно заданному вектору.
5. нормальное уравнение прямой: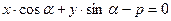 
Угол между двумя прямыми и условия параллельности и перпендикулярности двух прямых: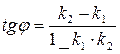 
Расстояние от точки до прямой: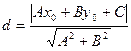 
16. Плоскость в пространстве.
Простейшей поверхностью является плоскость. Плоскость в пространстве можно задавать различными способами. Каждому из них соответствует определенный вид ее уравнения.
1. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору:
Точка Мо(Хо, Уо), вектор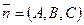 
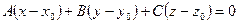
2. Уравнение плоскости, проходящей через три данные точки:
