60. Стационарные состояния, одномерные задачи

Дата: 2025-05-01; Просмотры: 2

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

§19. Стационарные состояния. Одномерные задачи

Пусть потенциальное поле не зависит от времени (стационарно) 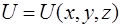. В этом случае уравнение Шредингера допускает разделение переменных пространственных 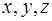и времени t. Действительно, представим волновую функцию в виде:Y=f (t)× Y₀(x, y, z), подставим это выражение в уравнение Шредингера и разделим обе части на Y.

Уравнение приобретает вид: 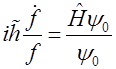, т.к. левая часть этого уравнения зависит только от времени, а правая – только от координат, то обе должны быть равны одной и той же постоянной Е, имеющей размерность энергии. В итоге получаем уравнения: 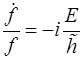(6.1)

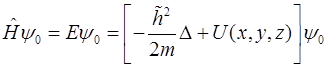. (6.2)

Решение (6.1) имеет вид: 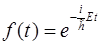(постоянный множитель оставляем в Y₀). Сравнивая с волной де Бройля, видим, что постоянная должна представлять энергию частицы. Это подтверждается видом уравнения (6.2), в котором в левой части стоит оператор Гамильтона (полной энергии частицы).

Решения вида: 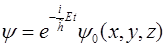определяют так называемые стационарные состояния. Легко видеть, что в таких состояниях и вероятность и плотность тока вероятности не зависят от времени, поскольку произведение .

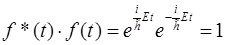Уравнение 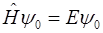называется уравнением Шредингера для стационарных состояний в отличие от временнóго (5.6). В дальнейшем (за исключением теории излучения) мы будем иметь дело, главным образом, с этим уравнением и Y₀ обозначать просто Y, не забывая, когда нужно умножать на временнýю экспоненту.

В случае, если волновая функция зависит только о одной координаты уравнение Шредингера принимает вид:

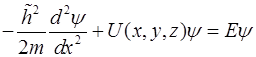или 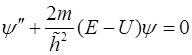. (6.3)

Это уравнение однородное уравнение второго порядка нам хорошо известно. Его решениями являются при E > U суперпозиция гармонических функций 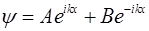, где 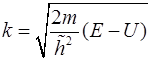(тип А), а при U > E суперпозиция экспонент с действительным показателем 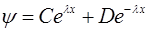, где 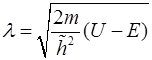(тип Б). Константы при экспонентах определяются в каждой задаче из конкретных граничных условий.

Рассмотрение одномерных задач более простых полезно т.к. уравнение Шредингера допускает разделение переменных, в декартовых координатах это бывает тогда, когда 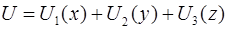, но нам придется иметь дело и с разделением переменных в сферических координатах.