Уравнение, описывающее скин-эффект
Исходим из уравнения Максвелла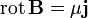 
и выражения для 
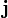по закону Ома: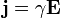 
Дифференцируя обе части полученного уравнения по времени, находим:
.
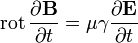
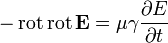Поскольку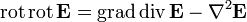 
и 
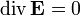окончательно получаем: 
.
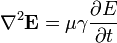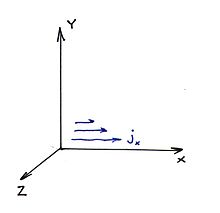
Скин-эффект в бесконечном проводнике с плоской границей.
Для упрощения решения предположим, что ток течёт по однородному бесконечному проводнику, занимающему полупространство y>0 вдоль оси X. Поверхностью проводника является плоскость Y=0. Таким образом,
,
.
Тогда
.
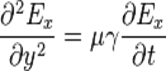В этом уравнении все величины гармонически зависят от t, и можно положить:
.
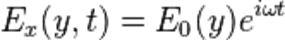Подставим это в наше уравнение и получим уравнение для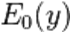 
:
.
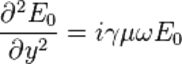Общее решение этого уравнения таково:
.
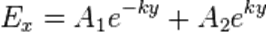Учитывая, что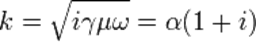 
, где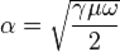 
, находим
.
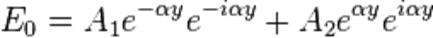При удалении от поверхности проводника (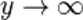 
) второе слагаемое неограниченно возрастает, что является физически недопустимой ситуацией. Следовательно, 
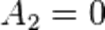и в качестве физически приемлемого решения остаётся только первое слагаемое. Тогда решение задачи имеет вид:
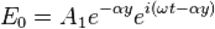Взяв действительную часть от этого выражения и перейдя с помощью соотношения 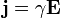к плотности тока, получим
.
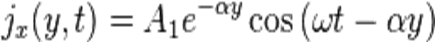Принимая во внимание, что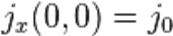 
— амплитуда плотности тока на поверхности проводника, приходим к следующему распределению объёмной плотности тока в проводнике:
.
39.ОБЩИЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ КВАЗИСТАЦИОНАРНЫХ ТОКОВ
40.ЭКСПЕРИМЕНТАЛЬНЫЕ ОСНОВЫ КВАНТОВОЙ ФИЗИКИ(МЕХАНИКИ)
Физ.и теория не могут быть построены на пустом месте .Теория строится на опытных законах их называют постулатами: 1)Постулат скорости света
Эксперименты
Опыт резерфорда по этим опытами установил, что малыми, а электроны движ. Около ядра и резерфорд предлагает модель атома.
1897-был открыт электрон Дж. Томсона.Атом-неделимый .
1911-резеофорд открыл ядро
Ультрафиолетовая катастрофа.
41.ВОЛНОВЫЕ СВОЙСТВА МИКРОЧАСТИЦ
42.ВЕРОЯТНОСТНЫЙ ХАРАКТЕР ОПИСАНИЯ ПОВЕДЕНИЯ МИКРОЧАСТИЦ
43. ПОСТУЛАТЫ КВАНТОВОЙ МЕХАНИКИ
Следуют из того что траектория микрочастица не может быть опред и считается что ее нет. Возникает вопрос: можем описать только вероятность т.е можем задаваться вопросом Чему равно вероятность того, что частица окажется внутри.
1)Первый постулата: Состояние любой частица в микромине задается нект функцией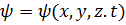 
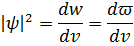
Квадрат модуля имеет смысл обнарж. Частица в ед. обьема.
dw-вер-ть однаружения частицы в dv
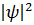-имеет смысл плотности вер-ти
Можем найти коэф волновой функции.
Осн задача квант механики нахождение волновой функции
2)Волновая функция подчиняется весьма общ диф ур-ю выраж принцип причины след. связи в микромире
Для одной частиц с массой m которое движется в потенциальном поле уравнение имеет вид:
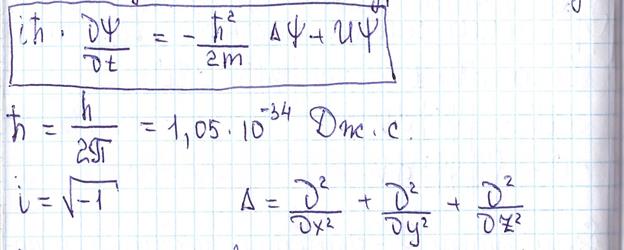
Надо задавать взаим-е частицы взаим ядром
Потенциал энергия неизвестна. Найти вер-ть. Волновая функция несет свою информацию
Квант мех нахождение вероятностей.( можно найти сред энергия)
Кван мех вычислила все параметры лазера. Лемб показал что должно изучать свер излучением.
4)динамические величина в квант мех представляются линейными самосопряженными операторами.
Представляется- это значит каждый динамич велич. Ставится соответствие линейным самосопряженный оператор
Динамич величина –это
44. МАТЕМАТИЧЕСКИЙ ФОРМАЛИЗМ КВАНТОВОЙ МЕХАНИКИ
45.МАТРИМЦА ПЛОТНОСТИ. ОПЕРАТОРЫ
Матрица плотности (оператор плотности, оператор матрица плотности, статистический оператор) – один из способов описания состояния квантовомеханической системы. В отличие от волновой функции, пригодной лишь для описания чистых состояний, оператор плотности в равной мере может задавать как чистые, так и смешанные состояния.
Использование оператора плотности становится необходимым, если состояние квантовомеханической системы по тем или иным причинам не может быть рассмотрено как чистое. Такое положение имеет место, в частности, в квантовой статистике. При этом оператор плотности оказывается естественным аналогом фигурирующей в классической статистической механике функции распределения плотности в фазовом пространстве. Кроме того, существует трактовка квантовомеханической процедуры измерения как перехода из исходного чистого состояния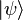 
в смешанное состояние
,
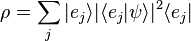где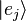 
суть отвечающие выбранному полному набору измеряемых величин базисные векторы.
46.СВОЙСТВА ВОЛНОВОЙ ФУНКЦИИ Не всякая мат-я ф-я может быть волн функ-й. К волн ф-ция опред определенной требование, из кот-й
1.Волн ф-я обязат однознач т.е одному аргументу соот только одно значение ф-ции
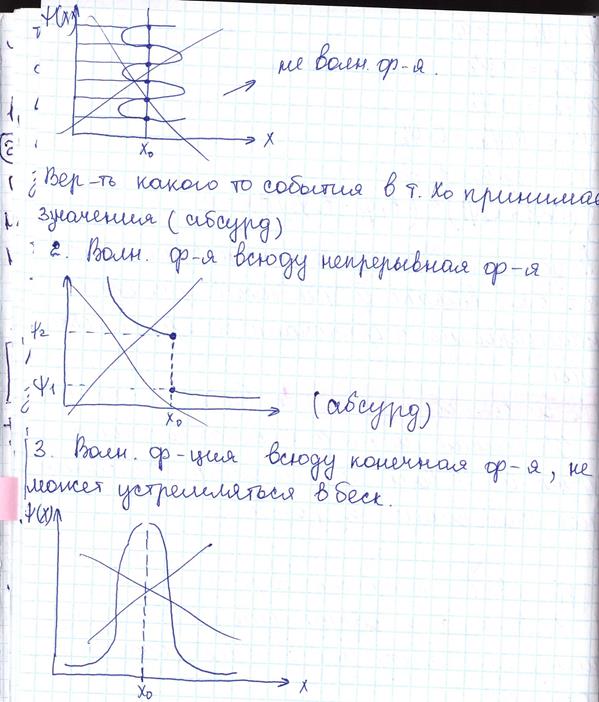
6. Волн ф-я имеет непрерывную первую производ по всем переменным от кот-х она зависит, т.к. в ур-е Шредингера входят вторая производная, если 1 производ испыт скачок, то 2 произв в т. Скачка не сущ-ет, что яв-ся абсурдом, т.к опыт Шредингера з-н природы