, где Uм – скалярный потенциал магнитного поля.

Дата: 2025-05-01; Просмотры: 2
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

В областях не занятых током (только для этих областей имеет смысл функция Uм) при постоянном значении магнитной проницаемости (m = const) скалярный потенциал магнитного поля подчиняется уравнению Лапласа:

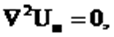
Линейный интеграл от напряженности магнитного поля по замкнутому контуру l, не охватывающему контура с током, равен нулю (закон полного тока). Поэтому (как в электростатическом поле), если условно принять равным нулю потенциал в некоторой точке Р (Uмр = 0), то разность потенциалов в точках А и Р будет равна потенциалу точки А:

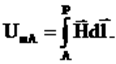
Однако, если выбрать такой путь интегрирования, который охватывает контур с током, правая часть уравнения (3.3) не будет равна нулю. Поэтому скалярный потенциал магнитного поля является функцией неоднозначной, но эта неоднозначность не оказывает влияния на расчет напряженности поля (i = const).Разность магнитных потенциалов между двумя точками называют падением магнитного напряжения между этими точками.

20.ПОТНЦИАЛ ДЛЯ ТОЧЕЧНОГО ЗАРЯДА.

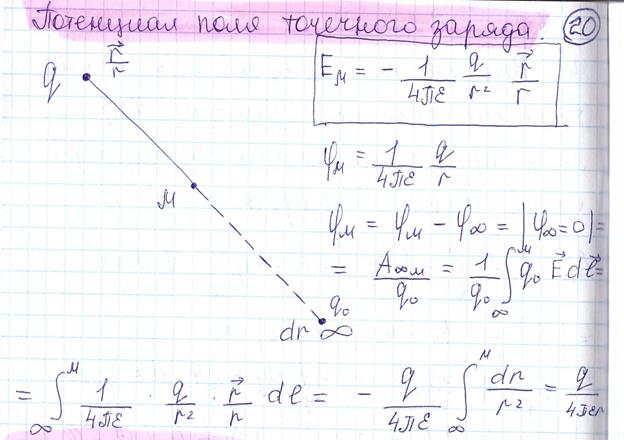
21.ПОТЕНЦИАЛ ПОЛЯ СИСТЕМЫ ЗАРЯДОВ

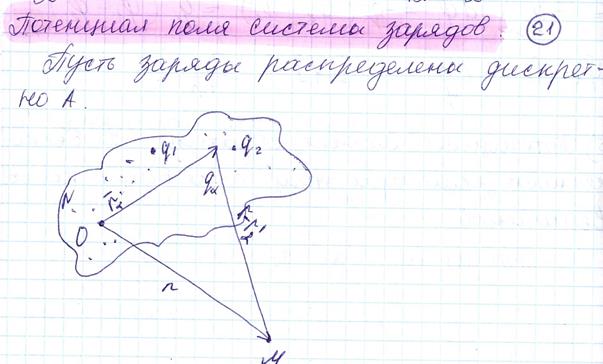
22.ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ДЛЯ СКАЛЯРНОГО ПОТЕНЦИАЛА

23.РАЗЛОЖЕНИЕ ПО МУЛЬТИПОЛОЯМ

24.ПРОВОДНИКИ В ЖЛЕКТРОСТАТИКЕ

 

25.ЭКРАНИРОВАНИЕ ПОЛЕЙ

26.ДИЭЛЕКТРИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ

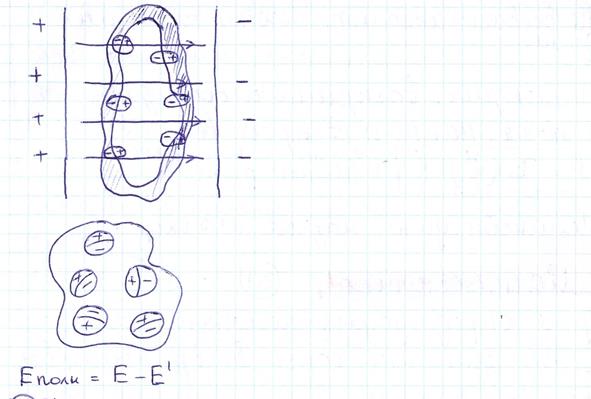
27.ПОЛЯРИЗАЦИЯ ДИЭЛЕТРИКОВ

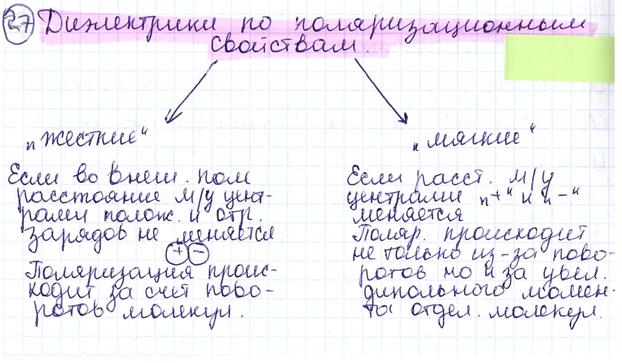
28.ЭНЕРГИЯ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ

Энергия электростатического поля - это энергия системы неподвижных точечных зарядов, энергия уединенного заряженного проводника и энергия заряженного конденсатора.

Если имеется система двух заряженных проводников (конденсатор), то полная энергия системы равна сумме собственных потенциальных энергий проводников и энергии их взаимодействия:

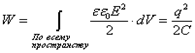
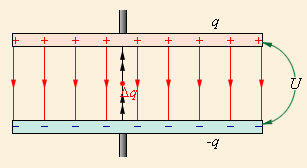
Энергия электростатического поля системы точечных зарядов равна: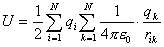

29.СОБСТВЕННАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА

Рассмотрим незаряженное тело. Если добавлять телу первый заряд, то работы совершаться не будет, потому что тело ещё нейтральное. Если же в тело внести второй заряд, то будет совершена работа электростатических сил по перемещению заряда к заряженному телу. При этом:

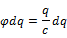
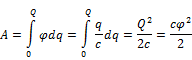
То есть при аддитивном сложении зарядов, общая энергия внесения в поле не подчиняется принципу суперпозиции, в отличие от общей потенциальной энергии.

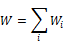
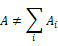
30.ЭНЕРГИЯ ВЗАИМОДЕЙСТВИЯ СИСТЕМЫ ЗАРЯДОВ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ

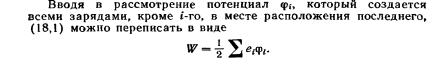
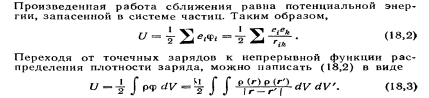
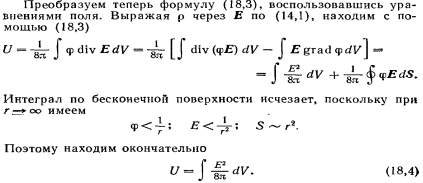
31. МАГНИТОСТАТИКА

 

32.СТОРОННИЕ СИЛЫ

Смещение под действием электрического поля зарядов в проводнике всегда происходит таким образом, что электрическое поле в проводнике исчезает и ток прекращается. Для протекания тока в течение продолжительного времени на заряды в электрической цепи должны действовать силы, отличные по природе от сил электростатического поля, такие силы получили название сторонних сил. Эти силы могут быть обусловлены химическими процессами, диффузией носителей тока в неоднородной среде, электрическими (но не электростатическими) полями, порождаемыми переменными во времени магнитными полями, и т. д. Всякое устройство, в котором возникают сторонние силы, называется источником электрического тока. Сторонние силы характеризуют работой, которую они совершают над перемещаемыми по электрической цепи носителями заряда. Величина, равная работе сторонних сил по перемещению единичного положительного заряда, называется электродвижущей силой (ЭДС) 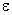, действующей в электрической цепи или на ее участке.Представим стороннюю силу 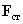, действующую на заряд q, в виде

,

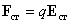где векторная величина 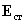представляет напряженность поля сторонних сил. Тогда на участке цепи ЭДС равна

.

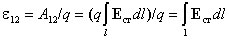Интеграл, вычисленный для замкнутой цепи, дает ЭДС, действующую в этой цепи,

.

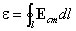Последнее выражение дает самое общее определение ЭДС и пригодно для любых случаев. Если известно, какие силы вызывают движение зарядов в данном источнике, то всегда можно найти напряженность поля сторонних сил и вычислить ЭДС источника. Физическая природа электродвижущих сил в разных источниках весьма различна.

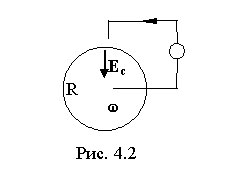
Рассмотрим пример. Пусть имеется металлический диск радиуса R (рис. 4.2), вращающийся с угловой скоростью 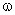. Диск включен в электрическую цепь при помощи скользящих контактов, касающихся оси диска и его окружности. Центростремительная сила 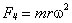, где m - масса электрона; r - расстояние от оси диска. Эта сила действует на электрон и поэтому 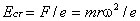, возникающая ЭДС равна

.

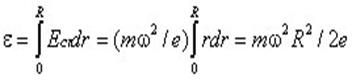33.ВЕКТОРНЫЙ ПОТЕНЦИАЛ

34.ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДЛЯ ВЕКТОРНОГО ПОТЕНЦИАЛА

35.СИММЕТРИЯ МЕЖДУ ЗАКОНАМИ ЭЛЕКТРОСТАТИКИ И МАГНИТОСТАТИКИ

36.КВАЗИСТАЦИОНАРНЫЕ ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ

37.ЗАКОНЫ ОМА С УЧЕТОМ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ

Изготовим, например, две катушки, совершенно одинаковые по размерам, форме и числу витков, одну из медной проволоки, а другую из нихромовой проволоки того же сечения и длины, и поместим их в одно и то же магнитное поле, например внутрь длинного соленоида, одинаково ориентировав катушки по отношению к направлению поля. Выключая магнитное поле, мы обнаружим в обеих катушках индукционные токи, но сила тока в медной катушке будет в 70 раз больше, чем в нихромовой. Это обстоятельство приводит к мысли, что при неизменных условиях опыта в катушке индуцируется определенная эдс, а сила тока, возникающего благодаря этому, определяется законом Ома и поэтому оказывается обратно пропорциональной электрическому сопротивлению цепи. для индукционных токов справедлив закон Ома(:

,

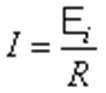где 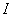– сила тока, 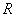– полное сопротивление цепи, т. е. сумма сопротивления индукционной катушки и сопротивления остальных частей цепи (реостата, лампочки, амперметра и т. д.), а через 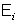обозначена э. д. с. индукции, остающаяся неизменной при изменении сопротивления цепи в наших опытах.

38. СКИН-ЭФФЕКТ

Поверхностный эффект, скин-эффект — эффект уменьшения амплитуды электромагнитных волн по мере их проникновения вглубь проводящей среды. В результате этого эффекта, например, переменный ток высокой частоты при протекании по проводнику распределяется не равномерно по сечению, а преимущественно в поверхностном слое.