14. Полная система уравнений максвелла в веществе
В среде сторонние электрические и магнитные поля вызывают поляризацию и намагничивание вещества, которые макроскопически описываются соответственно вектором поляризации P и вектором намагниченности M вещества, и вызваны появлением связанных зарядов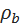 
и токов 
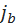. В результате поле в среде оказывается суммой внешних полей и полей, вызванных связанными зарядами и токами.
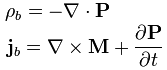
Поляризация P и намагниченность вещества M связаны с векторами напряжённости и индукции электрического и магнитного поля следующими соотношениями:
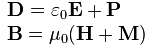
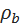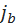Поэтому, выражая векторы D и H через E, B, и , можно получить математически эквивалентную систему уравнений Максвелла:
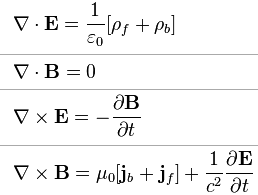
Индексом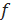 
здесь обозначены свободные заряды и токи. Уравнения Максвелла в такой форме являются фундаментальными, в том смысле, что они не зависят от модели электромагнитного устройства вещества. Разделение зарядов и токов на свободные и связанные позволяет «спрятать» в 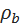, , 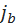а затем в P, M и, следовательно, в D, B сложный микроскопический характер электромагнитного поля в среде.
15 МОНОПОЛЬ ДИРАКА
16.ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ ДЛЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ. Поскольку электромагнитное поле является материальным объектом, оно обладает энергией.Формулу для объёмной плотности энергии электромагнитного поля можно получить путём сложения плотности энергии электрического и магнитного полей: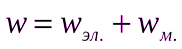 
.
Объёмная плотность энергии электромагнитного поля равна
.
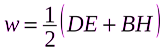Используя уравнения связи получаем:
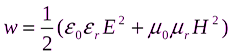. (31.3)
объёмные плотности энергии электрического и магнитного полей волны в любой момент времени одинаковы: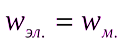 
можно показать, что модуль вектора Умова – Пойнтинга связан с объёмной плотностью энергии электромагнитного поля соотношением
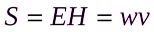, (31.5) где 
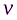- скорость распространения волны.
Электромагнитное поле может совершать работу по перемещению заряжённых частиц в пространстве. Объемная плотность мощности, то есть работа, совершаемая полем в единицу времени в единичном объеме пространства, равна
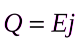, (31.6) где 
- плотность тока.
можно получить закон сохранения энергии электромагнитного поля
,
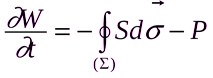Полная энергия электромагнитного поля в пределах области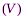 
;
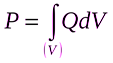
Закон сохранения энергии электромагнитного поля можно записать также в дифференциальной форме
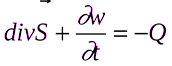
17. ЭЛЕКТРОСТАТИКА
18.УРАВНЕНИЯ МАКСВЕЛЛА В ЭЛЕКТРОСТАТИКЕ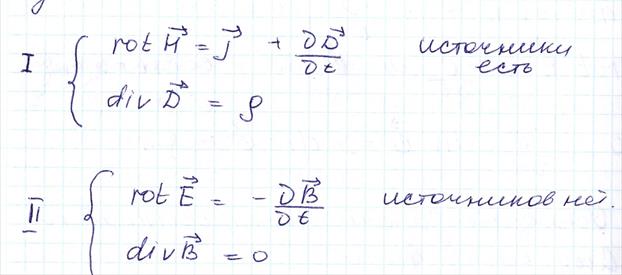 
5) 
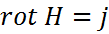
6) 
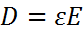
7) 
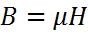
D,E,B.H с векторами)
19.СКАЛЯРНЫЙ ПОТЕНЦИАЛ
В той части пространства, где плотность тока d равна нулю (правая часть уравнения (3.4) равна нулю), магнитное поле можно рассматривать как потенциальное и напряженность магнитного поля можно представить в виде