Значение К для вычисления квадратичного отклонения( δ ) по амплитуде

Дата: 2025-06-02; Просмотры: 11
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0
0 1 2 3 4 5 6 7 8 9
0 - - 1,13 1,69 2,06 2,33 2,53 2,70 2,85 2,97
1 3,08 3,17 3,26 3,34 3,41 3,47 3,53 3,59 3,64 3,69
2 3,73 3,78 3,82 3,86 3,90 3,93 3,96 4,00 4,03 4,06
3 4,09 4,11 4,14 4,16 4,19 4,21 4,24 4,26 4,28 4,30
4 4,32 4,34 4,36 4,38 4,40 4,42 4,43 4,45 4,47 4,48
5 4,50 4,51 4,53 4,54 4,56 4,57 4,59 4,60 4,61 4,63
6 4,64 4,65 4,66 4,68 4,69 4,70 4,71 4,72 4,73 4,74
7 4,75 4,77 4,78 4,79 4,80 4,81 4,82 4,83 4,83 4,84
8 4,85 4,86 4,87 4,88 4,89 4,90 4,91 4,91 4,92 4,93
9 4,94 4,95 4,96 4,96 4,97 4,98 4,99 4,99 5,00 5,01
100 200 300 400 500 600 700 800 900 1000
5,02 5,49 5,76 5,94 6,07 6,18 6,28 6,35 6,42 6,48

Для нашего примера среднее квадратичное отклонение упрощенным методом: δ =±130-116 =±2,9 см

4,79

ЗНАЧЕНИЕ СРЕДНЕГО КВАДРАТИЧЕСКОГО ОТКЛОНЕНИЯ

1. С помощью среднего квадратического отклонения проводится оценка колеблемости вариационного ряда. В симметричном вариационном ряду в пределах значения одной сигмы от величины средней арифметической, т.е. М ± 1 δ находится 68,3% вариант от их общего числа.

В пределах двух сигм (М ± 2 δ) находится 95,5% вариант, в интервале трех сигм (М ± 3 δ) уже 99,7% вариант вариационного ряда. Таким образом, при нормальном распределении практически весь вариационный ряд укладывается в интервале ±3 δ от значения средней арифметической. Последнее известно как «правило трех сигм».

2. Среднее квадратическое отклонение применяется для оценки физического развития. Индивиды со значениями признака в пределах М±1 δ оцениваются как имеющие нормальное развитие, а этот интервал считают нормой. Индивиды со значением по признаку в пределах от +1 δ до +2 δ или от -1 δ до -2 δ оцениваются как имеющие развитие выше или ниже нормального, т.е. как субнорма. Если варианта находится в пределах от +2 δ до +3 δ или от - 2 δ до - 3 δ, то такой индивид расценивается как высокий или низкий (субаномалия).

3. Среднее квадратическое отклонение используется для оценки изменчивости нескольких вариационных рядов. В тех случаях, когда сравниваются ряды, имеющие одну и ту же систему измерений, (например, характеризуется только рост или масса тела) можно сделать выводы непосредственно по величине среднего квадратического отклонения. Однако при характеристике неоднородных рядов, когда значения одних представлены в метрах, других в килограммах, следует использовать коэффициент вариации:

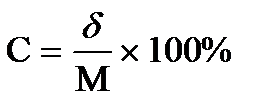
В практике приняты следующие критерии оценки коэффициента вариации:

· Низкий - если его величина не превышает 10,0%;

· Средний - если его величина колеблется в пределах от 10,0% до 20,0%;

· Высокий - если его величина больше 20,0%.

4. Среднее квадратическое отклонение применяется для оценки достоверности средних величин, о чем будет сказано ниже.