Построение логарифмических характеристик последовательно соединенных типовых динамических звеньев
Пусть передаточная функция части системы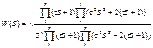 
Подставив вместо S jω найдем модуль, затем логарифмируя, найдем выражение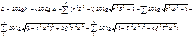 
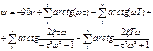
Эти формулы показывают, что результирующие характеристики определяются суммой логарифмических и фазовых характеристик типовых звеньев.
Устойчивость линейных систем
В процессе работы на систему действуют различные возмущающие силы, вызывающие ее отклонение от заданного закона движения. Если под влиянием возмущения система отклонилась от состояния равновесия и после прекращения действия внешнего возмущения снова вернулась в исходное состояние, то такая система устойчива.
Если под влиянием внешнего возмущения система будет отклоняться от состояния равновесия, а после прекращения действия возмущения система не возвращается в исходное состояние, а удаление системы с течением времени возрастает, то такая система называется неустойчивой.
В линейных системах отклонение при неустойчивом движении будет неограниченно возрастать.
Необходимое и достаточное условие устойчивости является выполнение требования, в соответствии с которым характеристическое уравнение системы должно иметь отрицательную вещественную часть. Наличие среди корней характеристического уравнения хотя бы одного корня с положительной вещественной частью свидетельствует о невыполнении этого условия, т.е. приводит к неустойчивости системы.
Устойчивость в линейной системе характеризуется затуханием переходного процесса. Т.к. затухание переходного процесса в свою очередь определяется только корнем характеристического уравнения и не зависит от воздействия, то устойчивость является внутренним свойством линейной системы.
Для определения устойчивости системы необходимому и достаточному условию нужно уметь находить корни характеристического уравнения. Это можно сделать просто для уравнения 1-го и 2-го порядков. Реальные системы десятых, сотых порядков. Поэтому для анализа устойчивости без нахождения корней характеристического уравнения, используют критерии устойчивости.
КРИТЕРИЙ УСТОЙЧИВОСТИ РАУСА-ГУРВЕЦА
Необходимым и достаточным условием устойчивости системы любого порядка без решения характеристического уравнения, по рассмотрению его коэффициентов, были сформулированы учеными Раусом и Гурвицом.
Руас сказал, что для выполнения условия устойчивости, а следовательно для расположения всех корней характеристического уравнения в левой полуплоскости , необходимо и достаточно, чтобы все коэффициенты характеристического уравнения были больше нуля.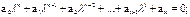 
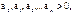
Гурвец дополнил, что для выполнения условия устойчивости, а следовательно, для расположения вех корней характеристического уравнения в левой полуплоскости, необходимо и достаточно, чтобы все n диагональных миноров матрицы были положительны.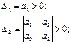 
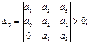
Критерий устойчивости Рауса и Гурвеца является алгебраическим, т.к. при их использовании задача определения знаков вещественных частей хар. уравнения сводится к выполнению общих алгебраических операций.
Критерий устойчивости найквеста
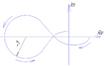
Этот критерий является графическим критерием. Правила, с помощью которых можно установить по АФЧХ разомкнутой системы необходимое и достаточное условие замкнутой системы. Если разомкнутая система устойчива, то для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы АФЧХ разомкнутой системы не охватывала на действительной оси координат от -1, j0. Второй случай соответствует неустойчивой САР. Эта точка называется критической. Если же АФЧХ проходит через точку (-1; j0), то САР будет находиться на границе устойчивости.
Если неустойчивая система имеет в правой полуплоскости петлю, то эта система будет устойчива в замкнутом состоянии и если АФЧХ разомкнутой системы описываемая концом вектора 1+W, при возрастании частоты от нуля до ∞ стрелка вектора обойдет критическую точку против часовой стрелки k раз. Это является необходимым и достаточным условием.
Качество и мощность простого управления
Вид передаточной функции позволяет судить о том, является ли система статической, либо аситатической, когда анализируется процесс регулирования, обусловленный управляющим воздействием, то обычно рассматривают ввод функции, относительно управляющего сигнала, а также ПФ
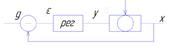
Предположим, что начальные условия нулевые(до приложения сигнала g(t)). Система находится в состоянии покоя
Для данной схемы система линейных ДУ имеет вид:
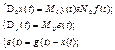,kz!!!! Pft,fkcz z!!!!!! Dct yf [eq!!!
Проектирование САР
При проектировании САР приходится решать такие задачи, как устойчивость САР. Устойчивость и качество САР противоречат друг другу. Удовлетворительное решение 1-ой задачи приводит к неудовлетворению 2-й задачи. Удовлетворительное решение задачи реализации требуемого запаса устойчивости и качества может быть достигнуты при одновременном использовании косвенных методов и изменения структуры системы, либо включением корректирующих устройств в прямую цепь системы, либо добавлением в цепь обратное связи.
Основное назначение корректирующих устройств – это изменение динамических свойств системы в направлении желаемых нами характеристик, что позволит нам усилить нужные характеристики только в той части системы, в которой это будет существенно.
Влияние корректирующих устройств на динамические свойства проявляется также в изменении фазовых характеристик. Использование корректирующих устройств на ряду с изменение коэффициента передачи в разомкнутой цепи и изменение порядка остатизма приводит к настройке характеристик, что и необходимо.
Физические основы коррекции состоят в следующем: Динамические свойства системы следует изменять с помощью корректирующих устройств так, чтобы приблизить их желаемым, но в этом случае обеспечить условия, при которых использовать элемент посредством ??посредством управления звеном выбранным звеном управления??.
Сигнал управления содержит составляющие, которые влияют на качественные показатели процесса регулирования. Эта составляющая оказывает стабилизирующее воздействие на их колебание в переходном процессе.