Характеристики динамических сдвигов
Частотные характеристики
Рассмотрим передаточную функцию, состоящую из n-го количества элементов.
(*)
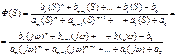Последовательность выражений позволяет найти амплитуду и фазу колебаний на выходе системы при гармоническом воздействии на ее входе.
Модуль этого выражения показывает, во сколько раз увеличивается или уменьшается амплитуда колебаний на выходе системы по сравнению с амплитудой колебаний на входе.
Аргумент вектора F(jω) описывает фазовый угол колебаний по отношению колебаниям на входе => (*) определяет частотную характеристику, называемую амплитудно-фазовой частотной характеристикой (АФЧХ).
АФЧХ строится на комплексной плоскости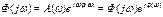 
j – мнимая единица.
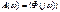- коэффициент, характеризующий изменение амплитуды при изменении частоты, при изменяющейся частоте, называется амплитудно-частотной характеристикой (АЧХ).
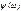дает представление о фазовом сдвиге выходных колебаний и он называется фазово-частотной характеристикой (ФЧХ)
АФЧХ: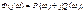 
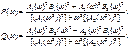
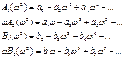
Вещественные или мнимые частотные характеристики связаны с АЧХ и ФЧХ следующим образом:
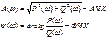
При анализе САР на устойчивость и качества процесса регулирования, а также при решении других задач, часто обращаются к ЛЧХ
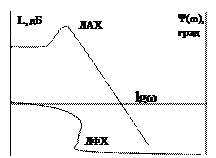
Усиление L(ω) = 20lg|Ф(jω)| = 20lgA(ω) [дБ] – является единицей логарифмической относительно величины. Изменения относительно двух величин в 10 раз соответствует изменению усиления на 20 дБ.
Известно, что АЧХ представляет собой отношение 2-х амплитуд: входного и выходного сигналов.
Переходная функция системы
Переходной функцией САР называется переходный процесс системы, вызванный единичным ступенчатым воздействием при нулевых начальных условиях. Используя понятие передаточной функции замкнутой системы и обратное преобразование Лапласа можно для переходной функции системы записать выражение: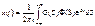 
. Если изображение управляющего сигнала G(S) является изображением единичного ступеньчатого воздействия, то его можно представить как 
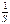, тогда выражение будет определять переходную функцию в следующем виде: 
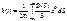- эта формула характеризует реакцию системы при единичном скачке и является переходной функцией. 