Движение и реорганизация систем
При первой же попытке представить себе как движутся тела, построенные подобно твердому телу - из каких-нибудь "точечных" элементов, занимающих устойчивые положения или потенциальные ямы в каком-нибудь поле (пусть даже фантастическом), обнаруживается неожиданная проблема, и приходится ее отчасти решать, отчасти обходить.
Дело в том, что потенциальная яма, в которой находится элемент, - это сумма полей, излученных другими элементами из других мест чуть раньше и прошедших некоторый путь. Поля движутся с конечной скоростью, поэтому, если тело привести в движение (например, все его элементы сразу), потенциальные ямы начнут двигаться с некоторым запаздыванием и будут отставать от элементов; они образуются там, где элементы были в момент излучения поля и откуда уже ушли. Элементы попадают "на склоны ям", и появляются силы, останавливающие движение. Движения по инерции не получается. Какими бы ни были поля и силы, создающие целостность тела, эта проблема остается как неизбежное следствие самой целостности и ограниченности скорости полей.
Целостность всякого тела и всякого процесса создается двусторонними связями между его частями, т.е обратными связями. Скорость связей при этом конечна, и всякий целый объект является в этом смысле системой обратных связей с т.н. "транспортным запаздыванием". Системы обратных связей вообще и такие системы в частности изучает теория авторегулирования. Этой теорией мы пользоваться не будем, но учтем, что занимаемся здесь свойствами, общими для систем с запаздывающими связями, создающими целостность.
Чтобы привести, например, все три диполя на рисунке 1 в совместное движение вправо или влево, нужно приложить к ним силы, выводящие диполи из устойчивых положений. Система будет двигаться лишь до тех пор, пока ее движут внешние силы. Поля будут всегда отставать от диполей, и будут действовать силы, движущие диполи назад к устойчивым положениям. Действие этих сил не прекратится, пока что-то не изменится и элементы не будут двигаться в "ямах". Что же должно измениться, как и почему? Чтобы эти силы не возникали вовсе, нужно, чтобы потенциальные ямы заранее, еще до начала движения, излучались туда, где окажутся элементы, когда поля дойдут от своих источников до "ям". Если же изменения начнутся после начала движения (что и происходит в системах), то эти силы будут действовать при ускорениях, выступая как силы инерции.
Пока поля и силы, создающие целостность тел, оставлялись в тумане, эта проблема не возникала. Теперь же, отмахнувшись от нее, мы не получим стройной картины движения. А обратив на нее внимание, попадаем в трудное положение. Ведь инерция считается фундаментальным свойством материи, а мы видим какую-то инерцию вместе с ее причиной. И избавиться от нее не можем. Это та же самая инерция или какая-то вторая? Пока лишь понятно, что она пропорциональна электромагнитной энергии в элементах и обратно пропорциональна квадрату скорости поля, но в наших системах, на первый взгляд, зависит и от других причин. Это та нить, которая ведет классическую физику к раскрытию причин инерции. Потянув за нее, можно размотать и весь клубок. Мы заниматься этим не будем. Сейчас не до открытий. Сначала нужно восстановить признание и авторитет классической физики. Рассмотрим это явление с другой целью и, обходя сложные пояснения, на совсем ином примере.
Пусть два автоматических подвижных объекта поддерживают расстояние между собой следующим способом. Действуя каждый по своим часам, они одновременно излучают периодические импульсы звука и, находясь на заданном (устойчивом) расстоянии, принимают их друг от друга точно в тот момент, когда излучают очередной импульс. Запаздывание сигнала к этому моменту означает, что расстояние велико, и объект движется, сокращая расстояние. При опережении - увеличивает расстояние.
Если эту пару привести в совместное движение, то задний в движении объект будет принимать сигналы с опережением, т.к. движется навстречу сигналам, и будет тормозить, пытаясь увеличить расстояние. Передний же объект будет получать сигналы с запаздыванием и тоже тормозить, пытаясь сократить расстояние. Объекты остановятся. Система не может двигаться по инерции.
Система иная, но явление то же и та же причина: конечная скорость сигналов и целостность системы.
Чтобы пара двигалась, нужно сдвинуть часы переднего объекта назад или заднего - вперед на некоторый временной интервал, так, чтобы компенсировать разность во времени хода сигналов вперед и назад при данной скорости. Точнее: сдвинуть во времени текущие в объектах процессы (приема-передачи и обработки сигналов). Тогда объекты будут поддерживать эту скорость и препятствовать ее изменению. Расстояние же между ними уменьшится так, чтобы сигналы снова проходили его взад-вперед за тот же период, несмотря на движение. Если скорость звука в воздухе равна "с", скорость объектов относительно воздуха - "v", то скорость сигнала относительно объектов будет равной в одну сторону c-v, в другую - c+v, а средняя скорость сигнала на всем пути окажется равной c(1 - v2/с2), потому расстояние между объектами тоже уменьшится пропорционально величине 1 - v2/с2. При движении в направлении, перпендикулярном расстоянию, размеры уменьшатся как корень квадратный из этой величины.
Итак, движение здесь сокращает размеры системы, а ее скорость определяется временным интервалом. Заметим, что, не зная, какова скорость объектов относительно среды, несущей звуковой сигнал, мы не сможем определить, как изменяется расстояние между ними. Поэтому, избегая такой неопределенности, в дальнейшем будем полагать, что все наши объекты погружены в какую-либо среду (газообразную, жидкую), которая и служит проводником электромагнитных или звуковых волн или сигналов. Кроме того, рассматривая движение электромагнитных объектов в средах, мы избегаем столкновения с теорией относительности, которая на движение в средах не распространяется.
Те же изменения будут происходить и в самоорганизующихся системах. Например, в системе из генераторов. В первый момент движения элементы выходят из устойчивых положений, и возникают силы, противодействующие движению. Но их "часы" (колебания в генераторах) синхронизируются сами, и через некоторое время установятся временные интервалы (разности фаз колебаний) между ними, точно соответствующие скорости. Ведь колебания в элементах синхронизируются излучениями, приходящими к ним друг от друга, а при движении излучение будет приходить к передним элементам с некоторым отставанием против прежнего, к задним - с опережением против прежнего. И, если раньше колебания были, например, одновременными, синфазными, то при движении колебания в задних элементах постепенно начнут опережать колебания в передних (каждый последующий в движении процесс опережает предыдущего на некоторый временной интервал).
Размеры систем тоже изменяются, уменьшаясь с увеличением скорости, поскольку уменьшается средняя скорость электромагнитного поля в промежутках между элементами, уменьшаются длины стоячих волн и расстояния между элементами После этого потенциальные ямы излучаются точно туда, где проходят движущиеся элементы, система движется по инерции, и силы противодействия не возникают.
Тройка диполей, показанная на рис.1, при движении вправо по инерции будет выглядеть, как показано на рис.2. Здесь диполь 3 (задний) опережает в своем вращении диполя 2. Его отрицательный заряд уже был вверху некоторое время назад, когда показанный на рисунке фрагмент волны проходил через него. Диполь 1 (передний) отстает в своем вращении. Его отрицательный заряд окажется вверху тогда, когда через него будет проходить волна, излученная диполем 2 и показанная на рисунке. Диполи 1 и 3 и в этом положении параллельны полю, но оно не параллельно плоскости рисунка и потому не показано. Таким образом, все три диполя движутся, оставаясь в устойчивых положениях. Но при ускорениях они не могут мгновенно повернуться относительно друг друга. Для этого нужно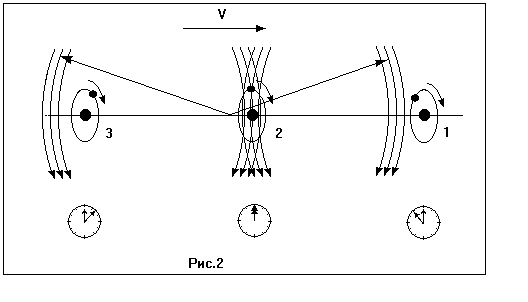 
двигать систему некоторое время, преодолевая силы устойчивости.
Ели бы все отрицательные заряды были здесь в верхнем положении, то на диполи 1 и 3 действовали бы силы, движущие их назад - в те участки поля, что показаны на рисунке. А их излучения оказались бы слева от диполя 2 - сзади, и на него тоже действовали бы такие силы. Кроме того, действовали бы силы, стремящиеся довернуть диполи в положения, показанные на рисунке 2. До тех пор, пока не сформируются временные интервалы, т.е. пока диполи не повернутся относительно друг друга, силы противодействия не исчезнут, и система не будет двигаться по инерции.
Системе диполей на рис.2 сопоставлена система часов, стрелки которых вращаются как бы вместе с диполями. Разность хода часов показывает временной интервал - относительное опережение или запаздывание местных процессов вращения и излучения. Изображая элементы (точнее: процессы в них) в виде часов в системе координат, можно одним значком показать и текущую фазу процесса, и его координаты. Так и сделаем потом.
В природе не существуют статические поля, способные удерживать элементы на расстояниях друг от друга, создавая объемные тела и структуры, и мы вынуждены полагать, что для этого необходимы когерентные волновые поля и процессы. Значит, целостность тела или структуры возможна лишь тогда, когда в их объеме присутствует некая система локальных "местных часов" - система единого внутреннего времени - объемный когерентный процесс. Любая пространственная структура, если цела, содержит в себе такую систему "часов". А изменение скорости структур связано с перестройкой этой системы единого времени и без нее не происходит.
Самоорганизующаяся система есть единый и цельный электромагнитный объект, поэтому конечный результат изменений, вызванных в ней движением, описывается преобразованиями Лоренца для электромагнитных объектов и процессов, движущихся в пустом пространстве или в той электромагнитной среде, в которую она помещена и сквозь которую движутся в ней волны. Мы привыкли понимать Лоренцево "местное время" как нечто сугубо теоретическое и абстрактное. Теперь же мы знаем объект, в котором можно разместить вполне реальные часы местного времени. Будем думать, что такие часы уже сделаны: к генераторам, составляющим систему, подключены электронные счетчики числа колебаний и их долей, и показания счетчиков выводятся на часовые табло.
Современная теория рассматривает преобразования Лоренца только как свойство пустого пространства-времени. Но лучше представлять себе, что электромагнитный объект находится в жидкой электромагнитной среде (в жидком диэлектрике или ферромагнетике), и что в движение приводится среда, а объект неподвижен. В таком случае объект также преобразуется по Лоренцу, но становятся наблюдаемыми те изменения, что происходят в нем при ускорениях среды - сокращение размеров и перестройка системы часов, а также "замедление времени" (т.е. замедление колебаний) и те силы, что возникают при ускорениях, увлекая объект вслед за средой и выступая в качестве сил инерции объекта относительно среды или инерции среды относительно объекта. Объект может быть любым, но лучше использовать самоорганизующиеся системы, т.к. в них, в отличие, например, от поля статических зарядов, имеются четко определенные расстояния и могут быть установлены часы местного времени. Мы рассмотрим это в другой главе.
С одной стороны, преобразования Лоренца описывают реорганизацию в электромагнитном объекте, производимую в нем движением, и это было известно. С другой стороны - временные интервалы управляют здесь скоростью объекта, выступают как причина и необходимое условие движений по инерции, и это нечто новое, ранее не известное. Противодействуют изменениям скорости те же силы, что создают целостность тела и его прочность, в естественных телах они достаточно велики, и, если бы реорганизации в них не было, скорость тел не могла бы меняться. Силы устойчивости, оказывается, создают инерцию движения. Если покоящийся объект подвергнуть такому изменению, создать в нем систему временных интервалов, то возникнут внутренние силы, движущие объект со скоростью, соответствующей этому изменению. Как выполняются при этом законы сохранения - нас здесь не интересует. Они так или иначе выполняются (в противном случае - только интересней).
Когда какое-либо тело приводится в движение внешней силой, то в месте приложения силы материал, например, сжимается, расстояния между элементами в нем уменьшаются, поля проходят эти расстояния быстрее, что приводит к некоторому повышению частоты колебаний в элементах сжатой части тела, в результате чего накапливаются временные интервалы (разности фаз) между колебаниями в сжатой и несжатой частях, и тело приходит в движение. Если Вы найдете способ управлять временными интервалами каким-то новым, еще не известным способом, то, может быть, откроете принципиально новый движитель. Но здесь у нас иная задача.
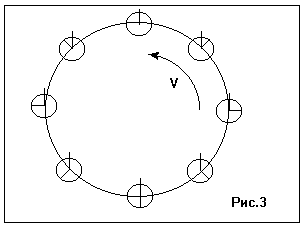Есть случаи, когда временные интервалы не могут изменяться. Тогда силы противодействия движению не исчезнут до тех пор, пока скорость системы не станет соответствовать временным интервалам. Например, если система имеет форму замкнутого кольца и вращается в своей плоскости вокруг центра, то сумма временных интервалов по периметру кольца может быть равной только целому числу периодов колебаний и не может меняться плавно. Поэтому кольцо имеет лишь дискретный ряд устойчивых скоростей вращения. Здесь мы видим механизм квантования движений.
На рисунке 3 показано такое кольцо. Элементы и процессы на нем представлены в виде часов, показывающих текущую фазу процесса. Вообще-то, квантуются все связанные волновыми полями движения, и мы не привыкли к этому лишь потому, что сильных волновых полей и очень больших скоростей нет в нашей практике.
Рассчитывая устойчивые формы такой вот структуры: кольцо из одинаковых электрически заряженных источников волновых излучений и противоположно заряженное тело в центре, получим серию устойчиво вращающихся в поле колец, диаметры которых и число элементов в которых (точнее: число мест в кольце) пропорциональны n2, т.е. такие структуры во многом подобны атому. И можем говорить, что принципиального различия между атомом и нашими самоорганизующимися структурами нет.
Мы не коснулись теперь лишь вопроса о спектрах излучения атомов. Современные авторы заявляют, что классическая физика и их объяснить не способна, и показывают нам это с помощью расчетов на классической модели атома в своем ее понимании. Однако, в этих расчетах не учитывается динамическое электромагнитное поле, излучаемое ядром и гасящее излучение электрона. Без этого частота вращения электрона не может быть вычислена. Но для начального объяснения этих спектров нам достаточно в наших вращающихся структурах лишь найти частоты, обратно пропорциональные квадрату числа n, среди множества частот колебаний и вращения, имеющих в них место. Такие частоты находятся.
Дело в том, что кольца в этих структурах вращаются с частотой, обратно пропорциональной кубу числа n. Это по в n раз быстрее, чем минимальная скорость кольца, состоящего из n2 элементов, поэтому сумма временных интервалов по их периметрам равна n периодам, т.е. кольцо связано воедино полем, которое содержит n пар вращающихся полюсов. При переходе структуры из одной устойчивой формы в другую имеют место два таких поля, а биения полей дадут искомые ряды частот. И мы можем говорить, что подобные ряды частот - тоже одно из свойств вращающихся самоорганизующихся структур с волновыми связями.
Когда "электроны" в этой структуре связаны в кольцо через волны, бегущие со скоростью света в пустоте, то скорость вращения кольца оказывается слишком большой для модели атома. Если же центральное тело похоже по проявлениям на электромеханический резонатор с медленными волнами, то вокруг него возможны медленные поверхностные волны, и скорость вращения колец, связанных этими волнами, может быть достаточно малой. В этом случае и один "электрон" оказывается связанным круговыми волнами как бы сам с собой и движется так же, как кольцо. Однако, такие структуры подробно не рассматривались.
Такие модели атомов способны образовывать модели молекул с общими электронными оболочками. Становится понятной тенденция к образованию общих оболочек. Теперь мы можем с помощью таких, пусть неполных, моделей еще несколько дополнить наше представление о микромире и твердом теле.
Итак, заявления о том, что классическая физика не способна объяснить строение атома и квантовость, тоже оказались весьма сомнительными. Говоря о квантах, мы пока не нашли оснований считать электромагнитное излучение потоком квантов, разве что условно. Мы видим здесь квантовость как свойство объектов, излучающих и принимающих излучение, но не самого излучения. Самоорганизующиеся системы природы имеют множество устойчивых состояний и, переходя из одного в другое, излучают и принимают энергию дискретными порциями.
Подобные поиски можно продолжать бесконечно. Но здесь не излагается курс классической волновой электромеханики. Сказанного достаточно.