10. Дано: . Найдите координаты вектора .
11. Найдите ГЦТ системы из двух материальных точек А(7; –6; 3), В(3; 11; –1), с массами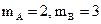 
.
12. Определить полярные координаты точек, симметричных точке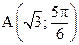 
относительно полюса и полярной оси.
13. Постройте комплексное число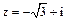 
на комплексной плоскости, найдите его модуль, аргумент и запишите его в тригонометрической форме.
14. Разложите на линейные множители многочлен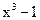 
.
15. Вычислите скалярное произведение векторов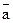 
и 
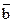, если 
.
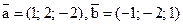16. Вычислите векторное произведение вектора 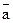на вектор 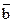, если 
.
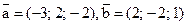17. Вычислить объем треугольной пирамиды, вершины которой А(–2; –1; 1), В(5; 5; 4), С(3; 2; –1), D(4; 1; 3).
18. Найдите нормальный вектор прямой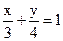 
.
19. Доказать, что прямая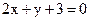 
пересекает отрезок, ограниченный точкам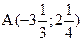и 
и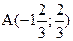 
.
20. При каком значении С прямая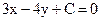 
принадлежит пучку 
.
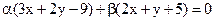21. Определите взаимное расположение плоскосте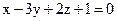й 
и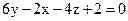 
.
22. Дана плоскость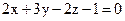 
. Найти для неё невязку точки А(1; 4; –3) .
23. Составить каноническое уравнение прямой, проходящей через точки А(1; –2; 2) и В(3; 4; –1).
24. Выясните взаимное расположение прямой и плоскост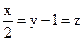и: 
и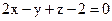 
.
25. Напишите уравнение окружности радиуса 2 с центром в точке С(2; 0).
26. Найдите фокусное расстояние гиперболы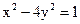 
.
27. Найдите уравнение оси симметрии параболы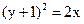 
.
Тест АГ-1. Вариант 16
1. Найдите каноническое разложение числа 840 в произведение простых множителей.
2. Найдите общий знаменатель дробе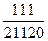й 
и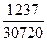 
.
3. Допустим, что Новый Год пришелся на понедельник. На какой день недели приходится в этом же году праздник 9-е мая?
4. Определите, разрешимо ли сравнение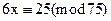 
и объясните почему да или почему нет.
5. Решите уравнение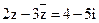 
.
6. Найдите остаток от деления многочлена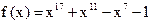 
на линейный двучлен 
.
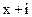7. В треугольнике АВС дано: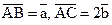 
, М – середина стороны ВС. Используя линейные операции с векторами, выразите вектор 
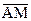через векторы 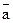и .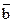
8. Найдите отношение, в котором точка С делит отрезок АВ координатной оси Ох, считая от точки А, если А(3), В(–9), С(–7).
9. Отметьте на координатной плоскости Оху следующие точки: А(3; 4), В(1; 2), С(–1; 2), D(4; –3).
10. Найдите расстояния от точки В( –2; 4; 3) до координатных плоскостей и координатных осей.
11. Найдите ГЦТ системы из двух материальных точек А(11; –6; 3), В(8; 8; –4), с равными массами.
12. Зная декартовые координаты точки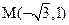 
, найдите её полярные координаты и укажите их на координатной плоскости.
13. Постройте на комплексной плоскости комплексное число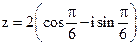 
, найдите его модуль, аргумент, и запишите его в тригонометрической форме.
14. Разложите степенной двучлен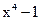 
на неприводимые множители над полем действительных чисел.
15. Даны векторы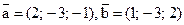 
. Вычислить 
.
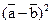16. С помощью векторного произведения двух векторов найдите площадь треугольника А(0; 2; –2), В(1; 4; –7), С(1; –5; 8).
17. Выяснить, компланарные ли векторы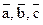 
, если 
.
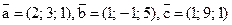18. Найдите координаты точки пересечения прямых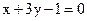 
и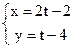 
.
19. Найдите нормирующий множитель для уравнения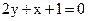 
.
20. Напишите уравнение пучка прямых с центром в точке М(–1; 2).
21. Найдите общее уравнение плоскости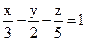 
с целыми коэффициентами, и её нормальный вектор.
22. Найти расстояние от плоскости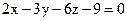 
до точки М(–5; 1; –5).
23. Задайте прямую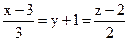 
пересечением двух плоскостей.
24. Убедитесь, что прямая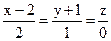 
параллельна плоскости 
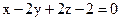, и найдите расстояние между ними.
25. Найдите директрисы эллипса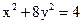 
.
26. Найдите каноническое уравнение гиперболы, если известны мнимая ось и эксцентриситет: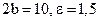 
.
27. Найдите фокальный параметр параболы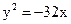 
.