8. Найдите на оси Ох координаты точки М, если А(–3), В(3) и .
9. На отрезке АВ найдите точку, которая делит его в отношении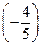 
, считая от точки 
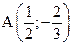, если 
.
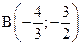10. Дано: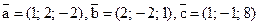 
. Найдите координаты вектора 
.
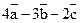11. Даны концы А(1; –4; 9) и В(–4; 0; 7) однородного стержня. Определить координаты его центра тяжести.
12. На плоскости дан квадрат со стороной 2 и полярная система координат, в которой полюсом служит центр квадрата, а полярный луч проходит через середину его стороны. Найдите полярные координаты вершин квадрата.
13. Найдите алгебраическую форму записи комплексного числа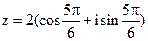 
.
14. Найдите все первообразные корни 6-й степени из 1 и составьте для них таблицу умножения.
15. Вычислить косинус угла между векторами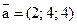 
и 
.
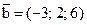16. Сила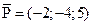 
приложена к точке М(4; –2; 3). Найдите момент этой силы относительно точки А(3; 2; –1).
17. Вычислите объем параллелепипеда, построенного на векторах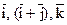 
как на его ребрах, используя геометрический смысл смешанного произведения векторов и его свойство линейности.
18. Найдите угловой коэффициент прямой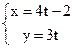 
.
19. Пересекает ли прямая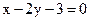 
отрезок, ограниченный точкам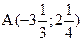и 
и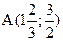 
?
20. Дан пучок прямых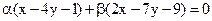 
. Найдите его центр.
21. Найдите общее уравнение плоскости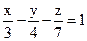 
с целыми коэффициентами, и её нормальный вектор.
22. Дана плоскость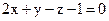 
. Найти отклонение от неё точки А(1; 3; –3).
23. Составить каноническое уравнение прямой, проходящей через точки А(1; –2; 2) и В(3; 1; –1).
24. Составить уравнение плоскости, проходящей через точку В(2; –1; –1), и перпендикулярной к прямой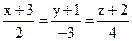 
.
25. Найдите эксцентриситет эллипса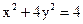 
.
26. Найдите каноническое уравнение гиперболы, если известны расстояние между директрисами и эксцентриситет: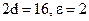 
.
27. Составьте уравнение параболы, если известны координаты её фокуса F(1; 2) и уравнение директрисы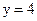 
.
Тест АГ-1. Вариант 15
1. Найдите все простые числа из промежутка [1510, 1520].
2. Найдите линейное представление НОД чисел 79 и 37.
3. Найдите последнюю цифру числа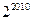 
.
4. В группе примитивных классов вычетов по модулю 8 решите уравнение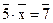 
.
5. Вычислите значение многочлена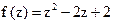 
при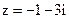 
.
6. Разложите многочлен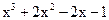 
на линейные множители.
7. По данным векторам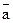 
и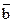 
, отложенными от одной точки, построить вектор 
.
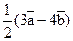8. Определить координаты середины отрезка CD, если С(–19), D(203).
9. Найдите расстояние между точкам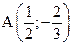и и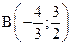 
, и координаты середины отрезка АВ.