6. Решите биквадратное уравнение .
7. Пусть О – точка пересечения медиан треугольника АВС, и ВD – одна из его медиан. Найдите линейное выражение вектора 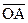 через вектор
через вектор 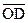 .
.
8. Найдите отношение, в котором точка С делит отрезок АВ координатной оси Ох, считая от точки А, если А(3), В(–5), С(–7).
9. Найдите расстояние между точками 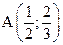 и
и 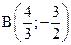 , и координаты середины отрезка АВ.
, и координаты середины отрезка АВ.
10. Дано: 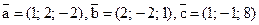 . Найдите координаты вектора
. Найдите координаты вектора 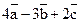 .
.
11. Найдите ГЦТ системы из двух материальных точек А(10; –6; 3), В(3; 8; –1), с равными массами.
12. Зная декартовые координаты точки 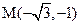 , найдите её полярные координаты и укажите их на координатной плоскости.
, найдите её полярные координаты и укажите их на координатной плоскости.
13. Постройте на комплексной плоскости комплексное число 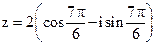 , найдите его модуль, аргумент, и запишите его в тригонометрической форме.
, найдите его модуль, аргумент, и запишите его в тригонометрической форме.
14. Разложите степенной двучлен 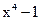 на неприводимые множители над полем действительных чисел.
на неприводимые множители над полем действительных чисел.
15. Даны векторы 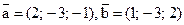 . Вычислить
. Вычислить 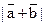 .
.
16. С помощью векторного произведения двух векторов найдите площадь треугольника А(–1; 2; –1), В(0; 4; –7), С(0; –5; 8).
17. Вычислите смешанное произведение векторов ортогонального базиса 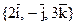 .
.
18. Найдите острый угол между прямыми 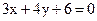 и
и 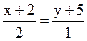 .
.
19. Определить, какие из следующих уравнений прямых являются нормированными: а) 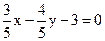 ; б)
; б) 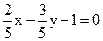 ;
;
в) 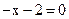 ; г)
; г) 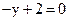 .
.
20. Дан пучок прямых 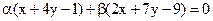 . Найдите его центр.
. Найдите его центр.
21. Определите взаимное расположение плоскостей 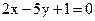 и
и 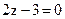 .
.
22. Дана плоскость 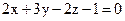 . Найти для неё невязку точки А(1; 2; –3) .
. Найти для неё невязку точки А(1; 2; –3) .
23. Найти параметрическое уравнение прямой, если её каноническое уравнение имеет вид: 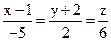 .
.
24. Составьте уравнение связки плоскостей с центром связки в точке А(1; 2; –1).
25. Найдите каноническое уравнение эллипса, если известны малая ось и эксцентриситет: 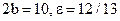 .
.
26. Докажите, что через начало координат нельзя провести касательную к гиперболе.
27. Постройте чертеж параболы 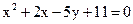 .
.
Тест АГ-1. Вариант 14
1. Найдите все простые числа из промежутка [310, 320].
2. Вычислите 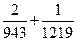 и запишите результат в виде несократимой дроби.
и запишите результат в виде несократимой дроби.
3. Найдите остаток от деления числа 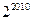 на 5.
на 5.
4. В кольце классов вычетов по модулю 8 решите линейное уравнение 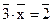 .
.
5. Решите уравнение 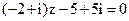 .
.
6. Решите уравнение 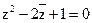 .
.
7. В равнобочной трапеции ABCD нижнее основание AD в два раза больше верхнего ВС, MN – средняя линия. Выразите вектор 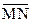 через векторы
через векторы 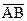 и
и 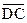 .
.








