6. Найдите остаток от деления многочлена на линейный двучлен .
7. По данным векторам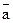 
и 
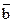, отложенными от одной точки, построить вектор 
.
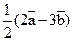8. Найдите на оси Ох координаты точки М, если А(–1), В(3) и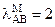 
.
9. Найдите расстояние между точкам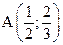и 
и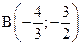 
, и координаты середины отрезка АВ.
10. Найти координаты орта вектора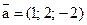 
.
11. Найдите ГЦТ системы из двух материальных точек А(11; –6; 3), В(3; 7; –1), с массами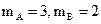 
.
12. Определить полярные координаты точек, симметричных точке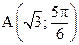 
относительно полюса и полярной оси.
13. Постройте комплексное число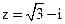 
на комплексной плоскости, найдите его модуль, аргумент и запишите его в тригонометрической форме.
14. Разложите на линейные множители многочлен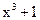 
.
15. Вычислите проекцию вектора 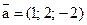на противоположный ему вектор.
16. Даны векторы: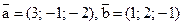 
. Найти 
.
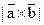17. Выяснить, компланарные ли векторы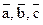 
, если 
.
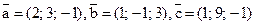18. Найдите угловой коэффициент прямой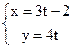 
.
19. Установить, лежит ли точка М(2; –3) и начало координат в одной или в разных полуплоскостях относительно прямой: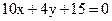 
.
20. При каком значении С прямая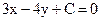 
принадлежит пучку 
.
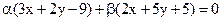21. Напишите общее уравнение какой-нибудь плоскости, проходящей через начало координат.
22. Найти нормирующий множитель для уравнения плоскости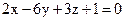 
.
23. Составить каноническое уравнение прямой, проходящей через точку М(1; 2; –3), и параллельной прямой
.
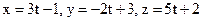24. Найдите уравнение пучка плоскостей, осью которого служит прямая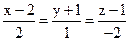 
.
25. Напишите уравнение касательной проходящей через точку М(1; 1) к эллипсу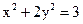 
.
26. Найдите каноническое уравнение гиперболы, если известны её асимптоты и фокальный параметр: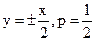 
.
27. Напишите уравнение касательной к параболе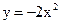 
в точке М(–1; –1).
Тест АГ-1. Вариант 12
1. Выпишите первые 11 простых чисел.
2. Найдите НОД чисел 72 и 96 с помощью алгоритма Евклида.
3. Найдите число примитивных классов вычетов по модулю 999.
4. Найдите все делители нуля в кольце классов вычетов по модулю 8.
5. Вычислите определитель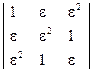 
, если 
.
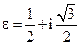6. Какие из следующих чисел являются корнями квадратного уравнения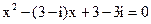 
: 
.
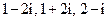7. В треугольнике АВС дано: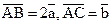 
, М – середина стороны ВС. Используя линейные операции с векторами, выразите вектор 
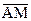через векторы 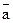и 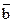.