2. Найдите общий знаменатель дробей и .
3. Выпишите приведенную систему вычетов по модулю 8.
4. В кольце классов вычетов по модулю 4 решите линейное уравнение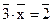 
.
5. Найдите алгебраическую форму записи частного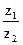 
комплексных чисел 
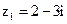и 
.
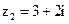6. Какие из следующих чисел являются корнями квадратного уравнения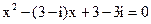 
: 
.
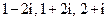7. По данным векторам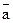 
и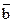 
, отложенными от одной точки, построить вектор 
.
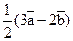8. Найдите расстояние АВ между точкам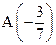и 
и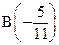 
.
9. Запишите в координатной форме орт вектора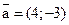 
.
10. Найти расстояние от точки А(12; –9; 4) до точки В(–2; 3; –2).
11. Найдите ГЦТ системы из трех материальных точек А(2; 12; 10), В(1; 4; 1), С(1; 2; 3), если массы вершин А, В и С, соответственно, образуют арифметическую прогрессию с разностью прогрессии, равной массе вершины А.
12. На плоскости дан квадрат со стороной 1 и полярная система координат, в которой полюсом служит вершина квадрата, а полярный луч проходит через вершину, противоположную полюсу. Найдите полярные координаты вершин квадрата.
13. Найдите алгебраическую форму записи комплексных чисел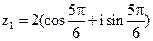 
и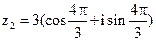 
, и найдите тригонометрическую форму записи их суммы и разности.
14. Найдите все первообразные корни 4-й степени из 1 и составьте для них таблицу умножения.
15. Даны векторы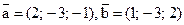 
. Вычислить 
.
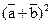16. Вычислите векторное произведение вектора 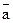на вектор 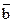, если 
.
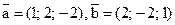17. Выяснить, компланарные ли векторы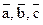 
, если 
.
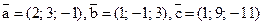18. Выяснить взаимное расположение прямых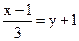 
и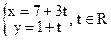 
.
19. Найдите расстояние от точки М(–6; 4) до прямой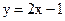 
.
20. Из пучка прямых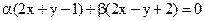 
выберите прямую перпендикулярную прямой 
.
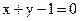21. Составить уравнение плоскости, проходящей через три точки: А(3; –1; 2), В(4; –1; –1) и С(2; 0; 2).
22. Даны уравнения трех плоскосте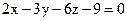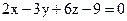й: 
, 
и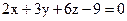 
. Докажите, что они пересекаются в одной точке.
23. Задайте прямую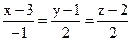 
пересечением двух плоскостей.
24. Составить уравнение плоскости, проходящей через точку В(1; –1; –1), и перпендикулярной к прямой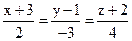 
.
25. Найдите фокусное расстояние эллипса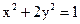 
.
26. Найдите фокальный параметр гиперболы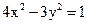 
.
27. Напишите уравнение касательной к параболе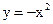 
в точке М(–1; –1).
Тест АГ-1. Вариант 8
1. Найдите наименьшее составное число большее 10, имеющее единственный простой делитель.
2. Докажите, что среди трех последовательных натуральных чисел найдется в точности одно число делящееся на 3.
3. Выпишите полную систему наименьших по абсолютной величине вычетов по модулю 10.